二重根号

→ 携帯版は別頁

== 二重根号 == ○　中学校で学んだように，a, x>0 のとき
x2=aならば $x=\sqrt{a}$
が成り立ちます．
【例1】
32=9だから $3=\sqrt{9}$

○　xとして根号を含む例を考えると，次の関係が成り立ちます．
$(\sqrt{2}+ \sqrt{3})^2=5+ 2\sqrt{6}$ だから $\sqrt{5+ 2\sqrt{6}}=\sqrt{2}+ \sqrt{3}$
$(\sqrt{3}-\sqrt{2})^2=5-2\sqrt{6}$ だから $\sqrt{5-2\sqrt{6}}=\sqrt{3}-\sqrt{2}$

○一般に

a,b>0 のとき，
$(\sqrt{a}+ \sqrt{b})^2=(a+ b)+ 2\sqrt{ab}$ だから $\sqrt{(a+ b)+ 2\sqrt{ab}}=\sqrt{a}+ \sqrt{b}$
a>b>0 のとき，
$(\sqrt{a}-\sqrt{b})^2=(a+ b)-2\sqrt{ab}$ だから $\sqrt{(a+ b)-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}$
が成り立つ．

［二重根号をはずすための基本公式］
(1)　a,b>0 のとき，
$\sqrt{(a+ b)+ 2\sqrt{ab}}=\sqrt{a}+ \sqrt{b}$

和がa+b，積がabなる２数 a,b を見つけると
$\sqrt{a}+ \sqrt{b}$
と変形できる．

(2)　a>b>0のとき，
$\sqrt{(a+ b)-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}$

和がa+b，積がabなる２数 a,b を見つけると
$\sqrt{a}-\sqrt{b}$
と変形できる．

※根号内にマイナス記号がある方の二重根号を外す場合は，a, bのうちの大きい方を前にして引き算をしないと $\sqrt{a}-\sqrt{b}$ が正の数にならないことに注意
例えば
$(\sqrt{3}-\sqrt{2})^2=5-2\sqrt{6}$
$(\sqrt{2}-\sqrt{3})^2=5-2\sqrt{6}$
のように２乗はいずれも等しいが
$\sqrt{3}-\sqrt{2}=\sqrt{5-2\sqrt{6}}$
$\sqrt{2}-\sqrt{3}=-\sqrt{5-2\sqrt{6}}$
のように，小さい根号が左にある方は符号が逆のものを表している．

※上の公式は (A+B)2=(A2+B2)+2AB の展開公式を用いて，
$\sqrt{(A^2+ B^2)+ 2AB}=A+ B$
もしくは，
$A=\sqrt{a},\hspace{3}B=\sqrt{b}$
とおいて
$\sqrt{(a+ b)+ 2\sqrt{a}\sqrt{b}}=\sqrt{a}+ \sqrt{b}$
とするものなので，2がなければ二重根号ははずれない．この 2 は二重根号をはずすために絶対必要な前提となるものなので，この頁では以下 2 のことを「金」に例えて解説する．　

※この頁では二重根号になっている式を変形して一重根号にすることを平凡な日常用語で「二重根号をはずす」と表現していますが，書物によっては二重根号の簡約とか，二重根号を解くと書かれていることもあります．

[1]　２はお金のように大切

【例２】

$\sqrt{8+ 2\sqrt{7}}$ の二重根号をはずすには

（解答）
○初めに内側の根号の前に 2 が付いていることを確かめる．この前提が満たされていないと，そもそも二重根号ははずれない．
○和が 8，積が 7 となる２数を求める　⇒ 7 と 1
○直ちに二重根号がはずれる
$\sqrt{8+ 2\sqrt{7}}=\sqrt{7}+ \sqrt{1}$
　形を整えて答
$\sqrt{7}+ 1$

【例３】

$\sqrt{7-2\sqrt{12}}$ の二重根号をはずすには

（解答）
○初めに内側の根号の前に 2 が付いていることを確かめる．この前提が満たされていないと，そもそも二重根号ははずれない．
○和が 7，積が 12 となる２数を求める　⇒ 4 と 3（4 >3だから4を前に持っていく）
○直ちに二重根号がはずれる
$\sqrt{7-2\sqrt{12}}=\sqrt{4}-\sqrt{3}$
　形を整えて答
$2-\sqrt{3}$

【問題１】　次の二重根号を外してください．各々正しいものを下の選択肢から選んでください．（クリックする）

(1)
$\sqrt{5+ 2\sqrt{6}}$

解説やり直す

$\sqrt{5}+ 1$ $\sqrt{5}-1$ $\sqrt{3}+ \sqrt{2}$ $\sqrt{3}-\sqrt{2}$ $\sqrt{2}-\sqrt{3}$

初めに中の根号の前に２がついていることを確かめる．
和が5で積が6となる2数を探す（和が6で積が5などと逆に考えてはいけない）

3と2

だから
$\sqrt{5+ 2\sqrt{6}}=\sqrt{3}+ \sqrt{2}$ …（答）

→閉じる←

(2)
$\sqrt{11+ 2\sqrt{18}}$

解説やり直す

$\sqrt{6}+ \sqrt{3}$ $\sqrt{6}-\sqrt{3}$ $3+ \sqrt{2}$ $\sqrt{5}+\sqrt{6}$ $\sqrt{6}-\sqrt{5}$

初めに中の根号の前に２がついていることを確かめる．
和が11で積が18となる2数を探す（和が18で積が11などと逆に考えてはいけない）

9と2

だから
$\sqrt{11+ 2\sqrt{18}}=\sqrt{9}+ \sqrt{2}=3+ \sqrt{2}$ …（答）

→閉じる←

(3)
$\sqrt{12+ 2\sqrt{27}}$

解説やり直す

$2+ \sqrt{3}$ $3+ \sqrt{3}$ $\sqrt{6}+ \sqrt{2}$ $\sqrt{10}+\sqrt{2}$ $2\sqrt{2}+2$

初めに中の根号の前に２がついていることを確かめる．
和が12で積が27となる2数を探す

9と3

だから
$\sqrt{12+ 2\sqrt{27}}=\sqrt{9}+ \sqrt{3}=3+ \sqrt{3}$ …（答）

→閉じる←

【問題２】　次の二重根号を外してください．各々正しいものを下の選択肢から選んでください．（クリックする）

(1)
$\sqrt{8-2\sqrt{15}}$

解説やり直す

$\sqrt{5}-\sqrt{3}$ $\sqrt{5}+ \sqrt{3}$ $\sqrt{3}-\sqrt{5}$ $2-\sqrt{2}$ $2\sqrt{2}-1$

初めに中の根号の前に２がついていることを確かめる．
和が8で積が15となる2数を探す

5と3

大きい方の5を前に書くと
$\sqrt{8-2\sqrt{15}}=\sqrt{5}-\sqrt{3}$ …（答）

→閉じる←

(2)
$\sqrt{7-2\sqrt{10}}$

解説やり直す

$\sqrt{5}+ \sqrt{2}$ $\sqrt{5}-\sqrt{2}$ $\sqrt{2}-\sqrt{5}$ $\sqrt{7}+ 1$ $2\sqrt{7}-1$

初めに中の根号の前に２がついていることを確かめる．
和が7で積が10となる2数を探す

5と2

大きい方の5を前に書くと
$\sqrt{7-2\sqrt{10}}=\sqrt{5}-\sqrt{2}$ …（答）

→閉じる←

[2]　金がないなら貯金から出す

$\sqrt{(a+ b)\pm 2\sqrt{a}\sqrt{b}}=\sqrt{a}\pm \sqrt{b}$ （マイナスのときは， $a\gt b$ ）
の公式を使うためには，内側にある根号の前に「必ず２」がなければなりません．

次のイメージで考える

(1) $\sqrt{5+ 2\sqrt{6}}$ ⇒金(2)がある⇒はずせる： $\sqrt{3}+ \sqrt{2}$
(2) $\sqrt{5+ \sqrt{6}}$ ⇒金(2)がない⇒はずせない：
(3) $\sqrt{5+ \sqrt{24}}$
⇒貯金の中に22=4があれば前に出す
$=\sqrt{5+ 2\sqrt{6}}=\sqrt{3}+ \sqrt{2}$

【内側の根号から貯金を引き出すには】
$\sqrt{k^2a}=k\sqrt{a}$
の公式を使います．中で2枚のものが外に出たら1枚になる
$\sqrt{2^2\times 3}=2\sqrt{3}$
$\sqrt{2^2\times 5}=2\sqrt{5}$
3枚あるときは2枚だけ引き出します
$\sqrt{2^3}=2\sqrt{2}$

【例３】
$\sqrt{8+\sqrt{60}}$ の二重根号をはずすには

（解答）
○内側の根号の前に金(2)がない→貯金(60)から引き出す
$\sqrt{8+\sqrt{60}}=\sqrt{8+\sqrt{2^2\times 15}}$
$=\sqrt{8+ 2\sqrt{15}}=\sqrt{5}+ \sqrt{3}$

【問題３】　次の二重根号を外してください．各々正しいものを下の選択肢から選んでください．（クリックする）

(1)
$\sqrt{10+\sqrt{84}}$

解説やり直す

$\sqrt{5}+ \sqrt{2}$ $\sqrt{6}+ 2$ $\sqrt{7}+\sqrt{3}$ $\sqrt{12}+\sqrt{7}$ $2\sqrt{2}+ 1$

○内側の根号の前に金(2)がない→貯金(84)から引き出す
$\sqrt{10+\sqrt{84}}=\sqrt{10+\sqrt{2^2\times 21}}$
$=\sqrt{10+ 2\sqrt{21}}=\sqrt{7}+ \sqrt{3}$ …（答）

→閉じる←

(2)
$\sqrt{7-\sqrt{40}}$

解説やり直す

$2+ \sqrt{3}$ $2-\sqrt{3}$ $\sqrt{6}+1$ $\sqrt{2}-\sqrt{5}$ $\sqrt{5}-\sqrt{2}$

○内側の根号の前に金(2)がない→貯金(40)から引き出す
$\sqrt{7-\sqrt{40}}=\sqrt{7-\sqrt{2^2\times 10}}$
$=\sqrt{7-2\sqrt{10}}=\sqrt{5}-\sqrt{2}$ …（答）

→閉じる←

(3)
$\sqrt{9-\sqrt{56}}$

解説やり直す

$\sqrt{5}-2$ $\sqrt{7}-\sqrt{2}$ $\sqrt{2}+\sqrt{7}$ $\sqrt{3}+\sqrt{6}$ $\sqrt{6}-\sqrt{3}$

○内側の根号の前に金(2)がない→貯金(56)から引き出す
$\sqrt{9-\sqrt{56}}=\sqrt{9-\sqrt{2^2\times 14}}$
$=\sqrt{9-2\sqrt{14}}=\sqrt{7}-\sqrt{2}$ …（答）

→閉じる←

(4)
$\sqrt{15+\sqrt{216}}$

解説やり直す

$3+ \sqrt{6}$ $\sqrt{10}+\sqrt{5}$ $2\sqrt{2}+\sqrt{7}$ $3\sqrt{3}+\sqrt{2}$

○内側の根号の前に金(2)がない→貯金(216)から引き出す
$\sqrt{15+\sqrt{216}}=\sqrt{15+\sqrt{2^2\times 54}}$
$=\sqrt{15+ 2\sqrt{54}}=\sqrt{9}+\sqrt{6}=3+\sqrt{6}$ …（答）

→閉じる←

[3]　金余りなら貯金に入れる

　 $\sqrt{(a+ b)\pm 2\sqrt{a}\sqrt{b}}=\sqrt{a}\pm \sqrt{b}$ （マイナスのときは，a>b）
の公式を使うためには，内側にある根号の前に「必ず２」がなければなりません．
　多ければよいというものでもなく，必ず2でなければならないので，余計なものがあっても困る．そこで，余った「金」は貯金します．

【金余り→貯金する】
$\sqrt{8+ 4\sqrt{3}}=\sqrt{8+ 2\sqrt{12}}=\sqrt{6}+ \sqrt{2}$
【2以外→貯金する, 2→貯金から出す】
$\sqrt{11+ 3\sqrt{8}}=\sqrt{11+ \sqrt{72}}=\sqrt{11+ 2\sqrt{18}}$
$=\sqrt{9}+ \sqrt{2}=3+ \sqrt{2}$

【問題４】　次の二重根号を外してください．各々正しいものを下の選択肢から選んでください．（クリックする）

(1)
$\sqrt{11+ 6\sqrt{2}}$

解説やり直す

$\sqrt{6}+ \sqrt{5}$ $3+\sqrt{2}$ $\sqrt{7}+ 2$ $\sqrt{6}+\sqrt{3}$ $2\sqrt{2}+ 1$

○内側の根号の前が2でない→金余りなら貯金する
$\sqrt{11+ 6\sqrt{2}}=\sqrt{11+ 2\sqrt{18}}$
$=\sqrt{9}+ \sqrt{2}=3+ \sqrt{2}$ …（答）

→閉じる←

(2)
$\sqrt{12-4\sqrt{5}}$

解説やり直す

$2-\sqrt{3}$ $\sqrt{5}-2$ $\sqrt{10}+\sqrt{2}$ $\sqrt{2}-\sqrt{10}$ $\sqrt{10}-\sqrt{2}$

○内側の根号の前が2でない→金余りなら貯金する
$\sqrt{12-4\sqrt{5}}=\sqrt{12-2\sqrt{20}}$
$=\sqrt{10}-\sqrt{2}$ …（答）

→閉じる←

(3)
$\sqrt{9-3\sqrt{8}}$

解説やり直す

$\sqrt{5}-2$ $\sqrt{2}-3$ $3-\sqrt{2}$ $\sqrt{6}-\sqrt{3}$ $\sqrt{3}-\sqrt{6}$

○2がなくて3がある→3を貯金に入れて2を貯金から出す
$\sqrt{9-3\sqrt{8}}=\sqrt{9-\sqrt{72}}$
$=\sqrt{9}-2\sqrt{18}=\sqrt{6}-\sqrt{3}$ …（答）

→閉じる←

(4)
$\sqrt{27+ 5\sqrt{8}}$

解説やり直す

$3+\sqrt{3}$ $5+ \sqrt{2}$ $\sqrt{10}+ \sqrt{5}$ $\sqrt{17}+ \sqrt{10}$

○2がなくて5がある→5を貯金に入れて2を貯金から出す
$\sqrt{27+ 5\sqrt{8}}=\sqrt{27+\sqrt{200}}$
$=\sqrt{27}+ 2\sqrt{50}=\sqrt{25}+ \sqrt{2}=5+ \sqrt{2}$ …（答）

→閉じる←

[4]　金がなくて貯金もないときは母に借りる

　 $\sqrt{(a+ b)\pm 2\sqrt{a}\sqrt{b}}=\sqrt{a}\pm \sqrt{b}$ （マイナスのときは，a>b）
の公式を使うためには，内側にある根号の前に「必ず２」がなければなりません．
　ここまで登場した例では，金(2)がない場合に貯金がありましたが，金もなく貯金もない場合にはどうすればよいのかを考えます．
$\sqrt{3+ \sqrt{5}}$
のように，金(2)もなく貯金(内側の根号の中に4)もない場合は，正しい変形になるように気をつけながら金(2)を作ります．
それは分母と分子の両方に２を掛けるということです．
$\sqrt{3+ \sqrt{5}}=\sqrt{\frac{6+ 2\sqrt{5}}{2}}$
$=\frac{\sqrt{6+ 2\sqrt{5}}}{\sqrt{2}}$
二重根号をはずすという問題は難しいのですが，分母の有理化という問題は比較的簡単なので後で何とかするとして，とりあえず分子の二重根号をはずす問題に専念します． $=\frac{\sqrt{5}+ 1}{\sqrt{2}}$
二重根号がはずれたら，分母を有理化すれば出来上がりです．
$=\frac{\sqrt{10}+\sqrt{2}}{2}$
※赤で示した式の変形において，分子の $3+ \sqrt{5}$ に勝手に2を掛けると式が変わってしまって等しい変形とはなりません．そこで，分母にも分子にも2を掛けて正しい変形となるようにするのがミソです．
　それはたとえ話で言えば「母親に無理をお願いして2だけ持ってもらう」「母に借りる」と言えば分かりやすいでしょう．

【金もなく貯金もない→母に借りる】
他の例：
$\sqrt{2+ \sqrt{3}}=\sqrt{\frac{4+ 2\sqrt{3}}{2}}$ $=\frac{\sqrt{4+ 2\sqrt{3}}}{\sqrt{2}}$
$=\frac{\sqrt{3}+ 1}{\sqrt{2}}$ $=\frac{\sqrt{6}+\sqrt{2}}{2}$

【問題５】　次の二重根号を外してください．各々正しいものを下の選択肢から選んでください．（クリックする）

(1)
$\sqrt{14+ \sqrt{75}}$

解説やり直す

$\frac{3\sqrt{5}+ \sqrt{2}}{2}$ $\frac{2\sqrt{5}+ \sqrt{2}}{2}$ $\frac{5\sqrt{3}+ \sqrt{2}}{2}$ $\frac{5\sqrt{2}+ \sqrt{6}}{2}$

○金(2)がなく貯金もないなら母（分母）に借りる
$\sqrt{14+ \sqrt{75}}=\sqrt{\frac{28+ 2\sqrt{75}}{2}}$
$=\frac{\sqrt{28+ 2\sqrt{75}}}{\sqrt{2}}=\frac{\sqrt{25}+ \sqrt{3}}{\sqrt{2}}$
$=\frac{5+ \sqrt{3}}{\sqrt{2}}=\frac{5\sqrt{2}+ \sqrt{6}}{2}$ …（答）

→閉じる←

(2)
$\sqrt{8+ \sqrt{63}}$

解説やり直す

$\frac{3\sqrt{2}+ \sqrt{14}}{2}$ $\frac{\sqrt{3}+ \sqrt{21}}{2}$ $\frac{2\sqrt{14}+ \sqrt{2}}{2}$ $\frac{4\sqrt{3}+ \sqrt{2}}{2}$

○金(2)がなく貯金もないなら母（分母）に借りる
$\sqrt{8+ \sqrt{63}}=\sqrt{\frac{16+ 2\sqrt{63}}{2}}$
$=\frac{\sqrt{16+ 2\sqrt{63}}}{\sqrt{2}}=\frac{\sqrt{9}+ \sqrt{7}}{\sqrt{2}}$
$=\frac{3+ \sqrt{7}}{\sqrt{2}}=\frac{3\sqrt{2}+ \sqrt{14}}{2}$ …（答）

→閉じる←

(3)
$\sqrt{6-\sqrt{35}}$

解説やり直す

$\frac{3\sqrt{7}-\sqrt{5}}{2}$ $\frac{\sqrt{14}-\sqrt{10}}{2}$ $\frac{2\sqrt{10}-\sqrt{2}}{2}$ $\frac{2\sqrt{2}-\sqrt{6}}{2}$

○金(2)がなく貯金もないなら母（分母）に借りる
$\sqrt{6-\sqrt{35}}=\sqrt{\frac{12-2\sqrt{35}}{2}}$
$=\frac{\sqrt{12- 2\sqrt{35}}}{\sqrt{2}}=\frac{\sqrt{7}-\sqrt{5}}{\sqrt{2}}$
$=\frac{\sqrt{14}-\sqrt{10}}{2}$ …（答）

→閉じる←

■備考■
[1]二重根号ははずれない方が多い

二重根号の問題がそこそこできるようになると「二重根号は，必ずはずせるんだ」と考えるかもしれませんが，それは正しくありません．
　生徒が出合う問題は「解ける問題」「はずせる問題」だけで，はずせない問題に触れる機会が少なく，「必ずはずれるんだ」という錯覚を持ってしまうのかもしれません．
　説明のために，
$\sqrt{a\pm 2\sqrt{b}}\hspace{10}(a,b\underline{\ge}1)$
の形の二重根号で $\sqrt{b}$ が無理数になるものだけを考え，これが
$\sqrt{m}+ \sqrt{n}}$
の形の（一重）根号になるかどうか調べてみる．

　 $\sqrt{b}$ が無理数という条件を付けないと，少し複雑になります．
　例えば， $\sqrt{1+ 2\sqrt{1}}$ は二重根号のように見えていますが，内側の根号内が平方数なので $\sqrt{1+ 2}=\sqrt{3}$ になります．
　同様にして， $\sqrt{a+ \sqrt{k^2}}$ の形をしたものは見かけは二重でも実質は二重根号ではありません．このようなものはここでは考えないことにします．…(##)

　和がaで積がbとなる２数m, nは，２次方程式
$x^2-ax+ b=0$ …(1)
の解になっているので，そもそも実数解を条件
$D=a^2-4b\underline{\ge}0$
すなわち
$1\underline{\le}b\underline{\le}\frac{a^2}{4}$ …(2)
を満たしていなければなりません．以下，この実数条件(2)を満たしているものだけを扱うと， $1\underline{\le}a,b\underline{\le}10$ の範囲で二重根号が外れるのは次の組合せだけです．
-- 表１ --

和	3	4	5	6	6	7	7	7	8	8	8	9	9	9	9	10	10
積	2	3	6	5	8	6	10	12	7	12	15	8	14	18	20	21	24

1≦a, b≦20の範囲で二重根号が外れるa, bの値を図示すれば次の丸印になります．（赤で示したのは実数条件の限界を表す放物線）

-- 図１ --

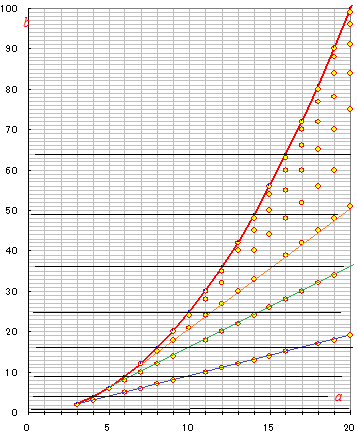
○1　これらの整数点は図１のように何本かの直線上に並びます．
　黒で示した横線は上の(##)で述べたb=1,4,9,16,25,···でbが平方数で元の式がそもそも二重根号とは言えないことを表しています．
　青の斜め線はb=a−1の直線になります．
　緑の斜め線はb=2a−4の直線になります．
　オレンジの斜め線はb=3a−9の直線になります．
一般に，各々のaに対して，低い方からk番目の点は $b=ka-k^2$ の直線上にあり， $k\underline{\le}\frac{a}{2}$ まで $\frac{a}{2}$ 本の直線が通っています．

○2　上の表１においてa=6の場合を例にとって解説する．

m+n=6
$mn=b\hspace{10}(1\underline{\le}b\underline{\le}\frac{a^2}{4})$
となる $b$ の値が幾つあるか調べるには，
1) m=1とおくと，n=6−1=5, b=mn=5
このとき
$\sqrt{6+ 2\sqrt{5}}=\sqrt{1}+\sqrt{5}=1+\sqrt{5}$
となる．
2) m=2とおくと，n=6−2=4, b=mn=8
このとき
$\sqrt{6+ 2\sqrt{8}}=\sqrt{2}+\sqrt{4}=\sqrt{2}+ 2$
となる．
3) m=3とおくと，n=6−3=3, b=mn=9
となってbが平方数になります．
*) 3<m<6のときは上記の解の順序を入れ換えたものになります．

このようにm+n=6のときはm=1, 2になれるから2組になります．

a=6の場合
　次の表で背景色が水色の組は二重根号がはずれ，赤字で示したのはbが平方数になっているもの．

和a	6	6	6
積b	5	8	9

　同様にして，a=10のとき
b=a−1
b=2a−4
b=3a−9
b=4a−16
のうちで下2個が平方数になっているので，運悪く二重根号がはずれるのは2組だけになります．

和a	10	10	10	10	10
積b	9	16	21	24	25

　a=6のように運よく多くの二重根号がはずれるものもありますが，a=10のように運悪くbの多くが平方数になってしまうものもあります．
　最も運がよい場合でも１つの値aに対して，二重根号がはずれるbの値は
$1\underline{\le}b\lt\frac{a}{2}$
すなわち
$1\underline{\le}b\underline{\le}\frac{a}{2}-1$
の $\frac{a}{2}-1$ 個です．
　a=6 → 2個
　a=10 → 4個（実際には2個）
　a=20 → 9個（実際には7個）
などとなり，aの値が大きくなるほど（実数条件を満たすもののうちで）二重根号がはずれる確率は薄くなります．

○3　図１において横の座標が偶数で実数条件の境界線 $b=\frac{a^2}{4}$ 上の点 $(a,\frac{a}{2})$ から出ている接線になっています．すなわち，これらの直線はaが偶数であるときに新たに追加される接線から成っています．

$y=\frac{x^2}{4}\rightarrow y\apos=\frac{a}{2}$
だから，接線の方程式は
$y-\frac{a^2}{4}=\frac{a}{2}(x-a)$
$y=\frac{a}{2}x-\frac{a^2}{4}$

[2]二重根号がはずれない例

a=6の場合
　次の表で背景色が水色の組は二重根号がはずれ，水色になっているものははずれないもの，赤字で示したのはbが平方数になっているものです．

和a	6	6	6	6	6	6	6	6	6
積b	1	2	3	4	5	6	7	8	9

例えば
$\sqrt{6+ 2\sqrt{2}}$
の二重根号をはずそうとすると，和が6で積が2となる2数を探すことになるので，解と係数の関係から
$x^2-6x+ 2=0$
の2つの解
$\sqrt{3+ \sqrt{7}},\sqrt{3-\sqrt{7}}$
を用いて
$\sqrt{6+ 2\sqrt{2}}=\sqrt{3+ \sqrt{7}}+\sqrt{3-\sqrt{7}}$
$=\frac{\sqrt{6+ 2\sqrt{7}}}{\sqrt{2}}+\frac{\sqrt{6- 2\sqrt{7}}}{\sqrt{2}}$
となります．さらに，この
$\sqrt{6+ 2\sqrt{7}},\sqrt{6-2\sqrt{7}}$
を2次方程式
$x^2-6x+ 7=0$
の2つの解を用いて求めようとすると
$\sqrt{6\pm 2\sqrt{2}}$
が登場して，堂々巡りになり，結局はずれません．
$\sqrt{6+ 2\sqrt{3}},\hspace{3}\sqrt{6+ 2\sqrt{6}}$
なども同様にして堂々巡りになり，はずれません．

[3]二重根号は，現在高校の教科書では扱われていない

　読者のやる気に水を注すような発言で申し訳ないのですが，この頁で取り上げた二重根号をはずす問題は「整数問題の処理」「論理的思考」の訓練にはなりますが，日常生活とのかかわりとなると非常に薄いものです．
　社会生活で実際に扱うデータは小数であることも多く，さらには二重根号，三重根号，３乗根，...12乗根など何でもありですが，それらはコンピュータで瞬時に処理できます．この頁で扱った「筆算だけで二重根号をはずす技術」というのは，日常生活ではほとんど出合わないと考えられます．

求めたいもの	筆算	Excel
$\sqrt{8+ 2\sqrt{3}}$ $ \sqrt{8+2\sqrt{3}} $	できない	=SQRT(8+2*SQRT(3)) =3.385867926
$\sqrt{3+ \sqrt{3+ \sqrt{3}}}$ $ \sqrt{3+ \sqrt{3+ \sqrt{3}}} $	できない	=SQRT(3+SQRT(3+SQRT(3))) =2.274934669
$\sqrt[3]{5+ \sqrt[3]{6}}}$ $ \sqrt[3]{5+\sqrt[3]{6}} $	できない	=(5+6^(1/3))^(1/3) =1.896125122

※このような訳で，二重根号のはずし方という問題は，現在のもしくは近未来の重点項目ではないと考えられますが「読者からの質問が多い」ので教材を置いています．

...（PC版）メニューに戻る

■［個別の頁からの質問に対する回答］[二重根号について／18.4.30］

「二重根号は，現在高校の教科書では扱われていない」ということに驚きました。また、それにも関わらずこのようにわかりやすく詳しい解説・問題を掲載してくださっていることに感謝します。ぜひ無くなさないでいただきたいです。
＝＞［作者］：連絡ありがとう．この教材を作ったころ（ゆとりの時代）には，学習指導要領で「二重根号をはずす計算は扱わないものとする」とされ，どんな事情があっても例外は許されないという意味の「～ものとする」で強く否定されていましたが，2018年現在の教科書では，発展学習として参考程度に触れられていることがあります．