|
2点間の距離の公式を用いて三角形の種類(二等辺三角形,直角三角形など)を求めるためには, 1 まず,三辺(AB,BC,CAなど)の長さを求めます.
(単に「二等辺三角形」と答えると,BC=CAの場合やCA=ABの場合があるので,どの2辺が等しいかを「AB=BCの」という形で明示することが大切です.)(2) 「AB=BC=CA」 ならば 「正三角形」などと答えます. (3) 「AB2+BC2=CA2」 ならば 「
(単に「直角三角形」と答えるのでなく,どの角が直角かも明示することが大切です.)
(4) 「AB2+BC2=CA2」かつ「AB=BC」 ならば 「AB=BCの直角二等辺三角形」などと答えます. (「直角」というのは角度の性質なので,距離の公式だけから直角を調べるには「ピタゴラスの定理」が成り立つかどうかで判断します.すなわち,「ピタゴラスの定理が成り立つ」→「直角三角形」,「ピタゴラスの定理が成り立たない」→「直角三角形でない」. ただし,この関係は三辺の長さを見ただけで分かるとは限りませんので,AB2+BC2=CA2などを「試してみる」しかありません. 例 √7,√8,√15なら(7+8=15だから)直角三角形です.√2,√3,√6なら(2+3<6だから)直角三角形ではありません.) |

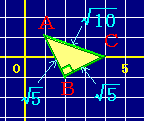 だから右図のようになる.
だから右図のようになる.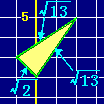 だから右図のようになる.
だから右図のようになる.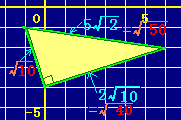 だから右図のようになる.
だから右図のようになる.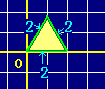 だから右図のようになる.
だから右図のようになる.