|
【内容】
この頁では,次のような問題の解き方を扱う. (1) 2直線 x−2y−7=0 …(1) 2x+y+1=0 …(2) の交点と点 (2 , 1) を通る直線の方程式を求めよ. (2) 直線 (2k+1)x+(k−2)y+(k−7)=0 は,定数 k の値にかかわらず定点を通ることを示し,定点の座標を求めよ. |
|
【要点と注意点】
○ ax+by+c+k(dx+ey+f)=0 は,定数 k の値にかかわらず2直線 ax+by+c=0 …(1) dx+ey+f=0 …(2) の交点を通る直線の方程式を表わす. ○ k=0 のときは,直線(1)を表わす.直線(2)はこの形式では表せない. ○ 直線 h(ax+by+c)+dx+ey+f=0 は h=0 のときは,直線(2)を表わす.直線(1)はこの形式では表せない. ※ 解き方の見通しを立てるためには,この結果は知っていなければならない. しかし,教科書に公式として示されている訳ではなく,証明せずに結果だけ使っても「示せ」という問題に対する答えとしては不十分と見なされることがあるので,答案の書き方に注意 (教科書に定理・公式として書かれていることは,(その定理・公式の証明を除けば)黙って使ってよいが,そうでないものは黙って使ってはいけない.) ※ 穴埋め問題のときは,この種の心配は無用 |
|
[例題1]
[解説]直線 (2k+1)x+(k−2)y+(k−7)=0 …(1) は,定数 k の値にかかわらず定点を通ることを示し,定点の座標を求めよ. 中学校で学んだように,方程式 Ax+By+C=0 は, A=0 かつ B=0 という特別な場合を除けば直線を表わす. ○ (1)において,2k+1=0 かつ k−2=0 とはならないから(一方が成り立てば他方は成り立たない),(1)は「直線を表わす」. ○ (1)を x−2y−7+k(2x+y+1)=0 と変形すると, x−2y−7=0 , 2x+y+1=0 となる (x , y) の値,すなわち2直線 x−2y−7=0 , 2x+y+1=0 の交点においては,(1)式は 0+0k=0 となり,定数 k がどんな値であっても成立する ⇔ (1)は「定点を通る」. 以上2つを続けて言うと,「定点を通る」「直線を表わす」となる. ○ 定点の座標は,連立方程式 x−2y−7=0 , 2x+y+1=0 を解くと求まり, (1 ,−3) …(答) ※ この問題の答案として,「 x−2y−7=0 , 2x+y+1=0 より, (1 ,−3) …(答)」とだけ書くと,間違ってはいないが「定数 k の値にかかわらず定点を通ることを示し」の部分に対する答案が示されていない. 他方で上で述べた解説のように書くのは,普通の高校生には少し荷が重い.そこで,次の[答案]のように書けばよい. 問題に書かれていることを信用すると,「定数 k の値にかかわらず定点を通る」はずだから,適当な k の値を代入して,初めに定点の座標を求める.[答案] k=2 のとき,(1)は 5x−5=0 となり,x=1 k=− のとき,(1)は - y−=0 となり,y=−3 (これが必要条件.もし定点があるとすればこれしかなく,これが解でなければ他には解はない.あとは,これが解であること,すなわち十分条件となることを示せばよい.) x=1 , y=−3 のとき, x−2y−7=0 , 2x+y+1=0 となるから,x−2y−7+k(2x+y+1)=0 は k の恒等式となる. 以上により,(1)は k の値にかかわらず定点 (1 ,−3) を通る. |
簡単な例でイメージ作り1 ○ 点 (3 , 4) を通り,傾き m の直線の方程式は ○ 点 (3 , 4) を通り,傾き m の直線の方程式はy−4=m(x−3) で与えられるが,この方程式を y−4+(-m)(x−3)=0 と見ると, m の値にかかわらず2直線 y−4=0 , x−3=0 の交点 (3 , 4) を通る直線を表わしている. 定数 m の図形的な意味は傾きで, m=0 のときは,直線 y−4=0 を表わす. m を限りなく大きく→∞(小さく→−∞)すると直線 x−3=0 に近づくが直線 x−3=0 に一致することはない. ○ 簡単な例でイメージ作り2 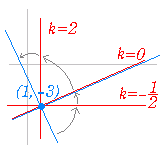 直線 (2k+1)x+(k−2)y+(k−7)=0 …(1) すなわち x−2y−7+k(2x+y+1)=0 …(1)’ は, ○ k=0 のとき,(1)’から直線 x−2y−7=0 を表わす. (この k の値は(1)’を見て,片方がうまく消える値を考えたもの) ○ k=2 のときは,(1)から直線 x=1 を表わす. (この k の値は(1)を見て,y の係数がうまく消える値を考えたもの) ○ k=− のときは,(1)から直線 y=−3 を表わす. (この k の値は(1)を見て,x の係数がうまく消える値を考えたもの) (この式では k の図形的意味は単純な傾きではないが,各々の直線からの影響の強さを 1 : k で表わしている. )
⇒ k の値を変えると「プロペラ」のように回る.
k を限りなく大きく→∞(小さく→−∞)すると直線 2x+y+1=0 に近づくが直線 2x+y+1=0 に一致することはない.○ 簡単な例でイメージ作り3 例えば 5x+6y+7=0…(2) に対して 2x+3y+4+k(5x+6y+7)=0…(3) (2+5k)x+(3+6k)y+(4+7k)=0…(3’) をk>0の範囲で考えてみると 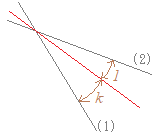 ア) 例えばk=0.01のような(1と比べて)微小な値のとき
ア) 例えばk=0.01のような(1と比べて)微小な値のとき2.05x+3.06y+4.07=0 となって,ほぼ(1)に近い形の式になり,(2)の影響はほとんどない. イ) 例えばk=100のような(1と比べて)大きな値のとき 502x+603y+704=0 方程式の両辺を100で割っても,方程式としては同じものを表すから 5.02x+6.03y+7.04=0 となって,ほぼ(2)に近い形の式になり,(1)の影響はほとんどない. ところで,ア)については,k=0を代入すると,ちょうど(1)を表すことができる. これに対して,イ)については,相当大きなkの値,例えばk=1000000を代入しても 5.000002x+6.000003y+7.000004=0 ちょうど(2)そのものには一致せず,近づくことができるだけである. これは,k:1に内分するときに,kをいくら大きくしても1が消えないからである. |
|
[例題2] 2直線 x−2y−7=0 …(1) 2x+y+1=0 …(2) の交点と点 (2 , 1) を通る直線の方程式を求めよ. [答案] 求める直線の方程式を x−2y−7+k(2x+y+1)=0 …(1) とおく. (1)が点 (2 , 1) を通るから, - 7+6k=0 k= …(2) このとき,直線の方程式は x−2y−7+(2x+y+1)=0 6x−12y−42+7(2x+y+1)=0 20x−5y−35=0 4x−y−7=0 …(答) 参考 この問題については,まず「2直線の交点の座標を求めて」,次に「2点を通る直線の方程式を求める」素朴な解き方も有効. 連立方程式(1)(2)の解は (1 ,−3) 2点 (1 ,−3) , (2 , 1) を通る直線の方程式は y+3=(x−1) y+3=4(x−1) 4x−y−7=0 …(答) |
|
*やや難しい
[例題3]
「すべての a, b で成立 ⇒ ある a, b で成立」の関係(⇒の先は必要条件)を利用して,捜査の範囲を絞る.すなわち,定点を先に求めてしまう.a, b が同時には 0 とならないとき,直線 (3a+b)x+(2a−3b)y+11b=0 …(1) は,定数 a, b の値にかかわらず定点を通ることを示し,定点の座標を求めよ. [答案] a, b が同時には 0 とならないから,3a+b=0 , 2a−3b=0 となることはなく,(1)は直線を表わす. a=1 , b=−3 のとき,(1)は 11y−33=0 となり,y=3 a=3 , b=2 のとき,(1)は 11x+22=0 となり,x=−2 x=−2 , y=3 のとき, 3x+2y=0 , x−3y+11=0 が成り立つから, a(3x+2y)+b(x−3y+11)=0 はどんな a ,b の値についても成り立つ. すなわち, (3a+b)x+(2a−3b)y+11b=0 はどんな a ,b の値についても成り立つ. 以上により,(1)は a , b の値にかかわらず定点 (−2 , 3) を通る. |
|
[問題1]
次の直線は定数 k の値にかかわらず定点を通る.この定点の座標を求めよ. (k+2)x+(2k−3)y+(4k−13)=0 …(1) |
|
[答案] k=−2 のとき, - 7y−21=0 y=−3 k= のとき, x−=0 x=2 ゆえに,(2 ,−3) を通る. ※参考 (k+2)x+(2k−3)y+(4k−13)=0 を変形すると 2x−3y−13+k(x+2y+4)=0 となり,この直線は 2x−3y−13=0 , x+2y+4=0 の交点 (2 ,−3) を通る. |
|
[問題2]
2直線 x−2y−7=0 …(1) x+3y+13=0 …(2) の交点と点 (−3 ,−3) を通る直線の方程式を求めよ. |
|
求める直線の方程式を x−2y−7+k(x+3y+13)=0 …(1) とおく.(1)が点 (−3 ,−3) を通る条件は - 3+6−7+k(−3−9+13)=0 …(2) (2)より k=4 このとき(1)は x−2y−7+4(x+3y+13)=0 5x+10y+45=0 x+2y+9=0 |
|
[問題3]
a, b が同時には 0 とならないとき,直線 (2a+b)x−(a−b)y=13a+2b …(1) は,定数 a, b の値にかかわらず定点を通る.この定点の座標を求めよ. |
|
a, b が同時には 0 とならないから,2a+b=0 , a−b=0 となることはなく,(1)は直線を表わす. a=−1 , b=2 のとき,(1)は 3y=−9 となり,y=−3 a=1 , b=1 のとき,(1)は 3x=15 となり,x=5 x=5 , y=−3 のとき, 2x−y−13=0 , x+y−2=0 が成り立つから, a(2x−y−13)+b(x+y−2)=0 はどんな a ,b の値についても成り立つ. すなわち, (2a+b)x−(a−b)y=13a+2b はどんな a ,b の値についても成り立つ. 以上により,(1)は a , b の値にかかわらず定点 (5 ,−3) を通る. |