...（携帯版）メニューに戻る...(ＰＣ版)メニューに戻る
*** 科目 ***
数Ⅰ・Ａ数Ⅱ・Ｂ数Ⅲ高卒・大学初年度
*** 単元 ***
式と証明点と直線円軌跡と領域三角関数
指数関数対数関数微分不定積分定積分
高次方程式数列漸化式と数学的帰納法
平面ベクトル空間ベクトル確率分布

※高校数学Ⅱの「点と直線」について，このサイトには次の教材があります．
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください．　 が現在地です．
↓◎内分点,外分点の図示
↓◎内分点,外分点の座標計算
↓◎内分点,外分点の座標
↓三角形の重心
↓2点間の距離の公式
↓点と直線の距離
↓三角形の形状問題
↓同(2)
↓1点と傾き→直線の方程式
↓2点→直線の方程式
↓2直線の平行条件
↓2直線の垂直条件
↓3点が1直線上にあるための条件
↓3直線が1点で交わるための条件
2直線の交点を通る直線の方程式

［例題1］
　３点 A(−2 , 1) , B(2 , 3) , C(4 , a) が同一直線上にあるように定数 a の値を定めよ．

【考え方1】
(I)　２点 A(x1 , y1 ) , B(x2 , y2 ) を通る直線の方程式は次の公式で得られる．
（ただし x1≠x2 ）

________y−y1=.y2−y1x2−x1nnnn(x−x1 ) …(1)

　そこで，「３点が一直線上にある」という条件を「点 C が直線 AB 上にある」と読み替えて，点 C が直線(1)の方程式を満たすようにすればよい．
(II)　点 C が直線 AB 上にあるかどうか調べるには，点 C の座標を直線 AB の方程式に代入すればよい．

【別解1の考え方】
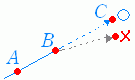
○　直線 AB の傾きが直線 AC の傾きと等しければ３点 A , B , C は一直線上にある．そうでなければ一直線上にない．
（右図では A,B,C の順に見えるがどの順に並んでいてもよい．）

○　さらに，直線の方程式とは次のように関係している．
________y−y1=.y2−y1x2−x1nnnn(x−x1 ) …(1)
　は
________.y−y1x−x1nnnn=.y2−y1x2−x1nnnn …(2)　と書くことができ

C(x3 , y3 ) が(2)を満たすための条件は
________.y3−y1x3−x1nnnn=.y2−y1x2−x1nnnn …(3)　となる．

※　このように C が AB 上にあるという条件は，AC の傾きが AB の傾きと等しいという条件と同じになる．