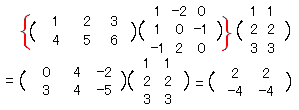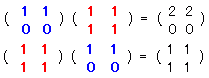行列の乗法の性質

← PC用は別頁

※高卒から大学初年度向けの「ベクトル，行列」について，このサイトには次の教材があります．
*** ベクトル ***
↓ ●ベクトル.行列の超基本 ●ベクトルの直交条件
●１次独立，１次従属，基底，次元，核，階数
*** 行列 ***
↓ ●逆行列(1) ●逆行列(2)
↓ ●転置行列，対称行列,対角行列，三角行列
●行列の階数
*** 行列式 ***
●行列式(1) ●行列式(2) ●行列式(3)
*** 一次変換 ***
●行列と一次変換 ●点の像と原像
*** 固有値 ***
↓ ●固有値.固有ベクトルの定義
↓ ●固有値と固有ベクトル(1) ●固有値と固有ベクトル(2)
●行列の対角化とは ●行列を対角化するには

== 行列の乗法の性質 ==
行列の積が定義できるとき，一般に

１　(積に関する) 結合法則が成立します。（ＡＢ）Ｃ=Ａ（ＢＣ）

　型については，［ｐ×ｑ型］［ｑ×ｒ型］［ｒ×ｓ型］→[ｐ×ｓ型] となります。(しりとりのルールです。)

２　(和の上への積の) 分配法則が成立します。 (Ａ＋Ｂ)Ｃ=ＡＣ＋ＢＣ
C(Ａ＋B)=ＣＡ＋ＣＢ

※　数字でも行列でも，積の上へ和は分配的ではありません。（分配法則は決して当たり前のことではありません。）

(ａ　×　ｂ)　＋　ｃ　≠　(a　＋　c)　×　(ｂ　+　ｃ)
(Ａ　×　Ｂ)　＋　Ｃ ≠　(Ａ　＋　Ｃ) × (Ｂ　+　Ｃ)

結合法則が成立する例：

は

に等しい。
※　結合法則や分配法則の成立を一般的に示すには，行列の型に応じて，成分の数だけ両辺を比較する「息の長～い計算」をします。(略)

左右の位置を入れ替えても積が定義できる場合について，

３［重要］　(積に関する) 交換法則は成立しません。すなわち，ＡＢ=ＢＡは必ずしも成立しません。

例

※　交換法則が成立するとは，「すべてのＡ，Ｂについて，ＡＢ＝ＢＡが成立する」ということで，１つでもＡＢ≠ＢＡとなる例があれば，交換法則は成立しないといいます。
したがって，交換法則が成立しないという主張にとって，ＡＢ＝ＢＡとなる例が幾つあっても関係ありません。

　たとえ話による解説：
「この部屋にいるのは全員男子である」という主張が間違っていることを示すには，「この部屋に少なくとも１人は女子がいる」ことを示せばよく，「この部屋にいるのが全員女子である」ことを示す必要はありません。

※Ａ，Ｂが正方行列でないときは，積の型が異なるためＡＢ≠ＢＡは自明です：

→　［３×２型］［２×３型］=［３×３型］になります。

→　［２×３型］［３×２型］=［２×２型］になります。

【要約】
　積が定義できるとき
「交換法則：×」，「結合法則：○」，「分配法則：○」

※行列の積については交換法則が成り立たないので，中学校以来慣れてきた文字式の変形を不用意に行わないように，細心の注意を払わなければならない．

ただし，何もできない訳ではなく，次に示すようにできる場合もあることもまた覚えておかなければならない．

２×２行列の積について，交換法則が成り立つ場合の例

(1)　ある行列Ａと単位行列Ｅ，零行列０は交換可能

$\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$ $=\begin{pmatrix}1& 0\\0& 1\end{pmatrix}\begin{pmatrix}a& b\\ c& d\end{pmatrix}$ $=\begin{pmatrix} a & b \\ c & d \end{pmatrix}$
だから，ＡＥ＝ＥＡはつねに成り立つ

$\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}$ $=\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ $=\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}$
だから，Ａ０＝０Ａはつねに成り立つ

(2)　ある行列のべき乗Ａ^mとべき乗Ａⁿは交換可能

ＡＡ²＝Ａ²Ａ＝Ａ³ やＡ²Ａ³＝Ａ³Ａ²＝Ａ⁵のように１つの行列のべき乗はつねに交換可能

(3)　対角行列と対角行列は交換可能

対角行列の積は，対応する対角成分の積で求められます
$\begin{pmatrix}a & 0 \\ 0 & b\end{pmatrix}\begin{pmatrix}x & 0 \\ 0 & y\end{pmatrix}$ $=\begin{pmatrix}ax & 0 \\ 0 & by\end{pmatrix}$
$\begin{pmatrix} x & 0 \\ 0 & y \end{pmatrix} \begin{pmatrix} a & 0 \\ 0 & b \end{pmatrix}$ $= \begin{pmatrix} ax & 0 \\ 0 & by \end{pmatrix}$
だから，ＡＥ＝ＥＡはつねに成り立つ

［問題］
　２×２行列について，任意の行列をＡ，Ｂ，Ｃ，単位行列をＥとするとき，次のうちで正しいものを選んでください．
（ただしいものをクリック）
(1)
　(Ａ+Ｂ)²＝Ａ²＋２ＡＢ＋Ｂ² は

つねに成り立つ成り立つとは限らない絶対成り立たない

解説

(Ａ+Ｂ)²＝Ａ²＋ＡＢ＋＋ＢＡ＋Ｂ² は成り立ちますが，交換法則が成り立たないので，ＡＢ＝ＢＡとは限らず，この式がＡ²＋２ＡＢ＋Ｂ²に等しいとは限りません．
ただし，絶対成り立たない訳ではなく，Ａ，Ｂをうまく選べば（Ｂ＝Ｅの場合など）成り立つ場合があります．⇒「成り立つとは限らない」

(2)
　(ＡＢ)²＝Ａ²Ｂ² は

つねに成り立つ成り立つとは限らない絶対成り立たない
解説

(ＡＢ)²＝ＡＢＡＢは成り立ちますが，交換法則が成り立たないので，ＡＢ＝ＢＡとは限らず，２番目の行列Ｂと３番目の行列が交換できるとは限らない．
ただし，絶対成り立たない訳ではなく，Ａ，Ｂをうまく選べば（Ａ＝Ｅの場合など）成り立つ場合があります．⇒「成り立つとは限らない」

(3)
　(ＡＢ)Ｃ＝Ａ(ＢＣ) は

つねに成り立つ成り立つとは限らない絶対成り立たない
解説

初めの解説に在るように，結合法則は常に成り立ちます．「交換法則：×」，「結合法則：○」，「分配法則：○」 ⇒「つねに成り立つ」

(4)
　(Ａ＋Ｂ)Ｃ＝ＡＣ＋ＢＣは

つねに成り立つ成り立つとは限らない絶対成り立たない

解説

初めの解説に在るように，分配法則は常に成り立ちます．「交換法則：×」，「結合法則：○」，「分配法則：○」 ⇒「つねに成り立つ」

(5)
　(Ａ＋Ｂ)(Ａ－Ｂ)＝Ａ²－Ｂ² は

つねに成り立つ成り立つとは限らない絶対成り立たない

解説

(Ａ+Ｂ)(Ａ－Ｂ)＝Ａ²－ＡＢ＋ＢＡ－Ｂ² は成り立ちますが，交換法則が成り立たないので，－ＡＢ＋ＢＡ＝０とは限らず，この式がＡ²－Ｂ²に等しいとは限りません．
ただし，絶対成り立たない訳ではなく，Ａ，Ｂをうまく選べば（各々が対角行列の場合など）成り立つ場合があります．⇒「成り立つとは限らない」

(6)
　(Ａ＋Ｅ)²＝Ａ²＋２Ａ＋Ｅは

つねに成り立つ成り立つとは限らない絶対成り立たない

解説

ある行列Ａとそのべき乗Ａⁿおよび単位行列Ｅや零行列０とはつねに交換可能です．この問題では，　(Ａ＋Ｅ)²＝(Ａ＋Ｅ)(Ａ＋Ｅ)＝Ａ²＋ＡＥ＋ＥＡ＋Ｅ²＝Ａ²＋2Ａ＋Ｅはつねに成り立ちます．⇒「つねに成り立つ」

［注］直前にPC版から入られた場合は，自動転送でスマホ版に来ていますので，ブラウザの［戻るキー］では戻れません（堂々巡りになる）．下記のリンクを使ってメニューに戻ってください．

...（携帯版）メニューに戻る

...（PC版）メニューに戻る