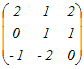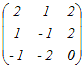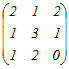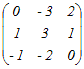|
�������
�y�s�x�N�g���C��x�N�g���z
�Ⴆ�C���̍s���A�Ƃ���Ƃ��C 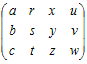  �C �C �C �C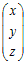 �C �C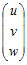 �@�܂��CA�͂R�̍s�x�N�g�� �y�ꎟ�Ɨ��C�ꎟ�]���z ���s�x�N�g���܂��͗�x�N�g���i�̑g�j, , , ...�ɂ��āC �@�ꎟ�Ɨ��łȂ��Ƃ��C�ꎟ�]���ł���Ƃ����܂��D ������x�N�g���i�̑g�j���C�ꎟ�Ɨ��ł���Ƃ��C �ǂ̃x�N�g�����C���̃x�N�g���̈ꎟ�����ɂ���ĕ\�����Ƃ͂ł��܂���D ��cp+cq+... �@�t�ɁC����x�N�g���i�̑g�j���C�ꎟ�]���ł���Ƃ��C �����ꂩ�̃x�N�g���́C���̃x�N�g���̈ꎟ�����ɂ���ĕ\�����Ƃ��ł��܂��D =cp+cq+...
�y��z
�y�s��{�ό`�C���{�ό`�z�@���̍s��A���S�����s�x�N�g��, , �̑g�ɂ���čl����Ƃ��C 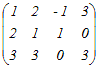 �ƂȂ��Ă��܂��D���������āC�����̍s�x�N�g���͈ꎟ�Ɨ��ł͂Ȃ��C�ꎟ�]���ł��D �@����ʂɂS�����x�N�g���ł́C�ꎟ�Ɨ��ȃx�N�g���͑����Ă��S�ł����C���̗�̂悤�ɂ���x�N�g�������̃x�N�g���̈ꎟ�����ŕ\�����Ƃ��́C�ꎟ�Ɨ��ȃx�N�g��������������Ȃ��Ȃ��Ă��邱�Ƃ�����܂��D �@�܂��C�s��A���R������x�N�g��, , , �̑g�ɂ���čl����Ƃ��C =− =− �ƂȂ��Ă��܂��D���������āC�����̗�x�N�g���͈ꎟ�Ɨ��ł͂Ȃ��C�ꎟ�]���ł��D �@����ʂɂR�����x�N�g���ł́C�ꎟ�Ɨ��ȃx�N�g���͑����Ă��R�ł����C���̗�̂悤�ɂ���x�N�g�������̃x�N�g���̈ꎟ�����ŕ\�����Ƃ��́C�ꎟ�Ɨ��ȃx�N�g��������������Ȃ��Ȃ��Ă��邱�Ƃ�����܂��D �y�ꎟ�Ɨ��ȃx�N�g���̌��z �����̍s��A�̂悤�ȂR�s�S��̍s��ł� 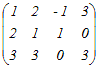 �@�܂��C�s�x�N�g���Ƃ��Ď��o���ƁC�S�����x�N�g���ƂȂ�̂ŁC�ꎟ�Ɨ��ȃx�N�g���̌��͑����Ă��S�܂łł��D �ˁ@�ȏォ��C�R�~�S�s����s�x�N�g���܂��͗�x�N�g���Ƃ��Ď��o���Ƃ��C�ꎟ�Ɨ��ȃx�N�g���̌��́C�s�Ɨ�̂������Ȃ����F�R�ȉ��ł��D �ˁ@��ʂɁC���~���s��ł���s�x�N�g���܂��͗�x�N�g���̂����ňꎟ�Ɨ��Ȃ��̂̌��́C���Ƃ��̂����ŏ��������ȉ��ƂȂ�܂��D ���s��̍s�i��j�ɑ��āC���̑�����s�����Ƃ��s�i��j��{�ό`�Ƃ����܂��D
���̕ό`�́C�A���������𐳂����ό`����Ƃ��ɁC�W���s��ɉ����邱�Ƃ̂ł���ό`���܂Ƃ߂����̂ł��D
�E�Q�̍s�i��j�����ւ���D
�E�P�̍s�i��j��萔�{�i���O�j����D
�Ȍ�̕ό`�̌��ʂ���ǂ����邽�߂ɁC
�E�P�̍s�i��j�ɑ��̍s�i��j�̒萔�{�i���O�j��������.
���s��{�ό`�ɂ������ẮC�s�x�N�g���̐����̂����ŁC�����猩�ĂO�łȂ��ŏ��̐������P�ƂȂ�悤�ɁC  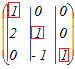 ����s�i��j�x�N�g�������̍s�i��j�x�N�g���̈ꎟ�����ŕ\�����Ƃ������� =cp+cq+... �́C �s�i��j��{�ό`�ɂ���ė�x�N�g���ɂȂ� �Ƃ������ƂƓ����Ȃ̂ŁC�s�i��j��{�ό`���J��Ԃ����Ƃ��ɁC��x�N�g���ɂȂ炸�Ɏc�����s�i��j�x�N�g���̌����s��̂����ňꎟ�Ɨ��Ȃ��̂̌��ł��D
�y�s��̊K���̋��ߕ��z
���s��̊K���Ƃ́C����s��̗�x�N�g���i�܂��͍s�x�N�g���j�̂����ňꎟ�Ɨ��Ȃ��̂̍ő���ł��D
�@�s�i��j��{�ό`�ɂ���āC�s�i��j�x�N�g���𐬕����Ȃ�ׂ���������������Ƃ��Ɂi�O�ɂ��āj�C
�@�������Ɏc�����s�i��j�x�N�g���̌����K��
�y��P�z
�E�Q�s�ڂɂP�s�ڂ�������D�@���̍s��̊K�������߂Ă��������D  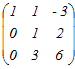 �@�R�s�ڂ���Q�s�ڂ̂R�{�������D  ��ʉ��� �E�Q��ڂ���P��ڂ������D �@�R��ڂɂP��ڂ̂R�{�𑫂��D 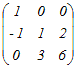 �@�R��ڂ���Q��ڂ̂Q�{�������D 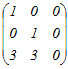
�y��Q�z
�E�P�s�ڂƂQ�s�ڂ����ւ���D�@���̍s��̊K�������߂Ă��������D 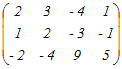 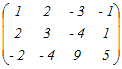 �@�R�s�ڂɂP�s�ڂ̂Q�{�𑫂��D 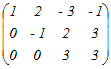   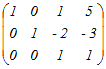 |
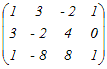 �̊K���́C���̂ǂꂩ�D
�̊K���́C���̂ǂꂩ�D
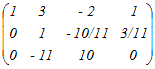

 �̊K����
�̊K����

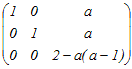
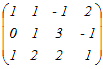 �̊K���́C���̂ǂꂩ�D
�̊K���́C���̂ǂꂩ�D

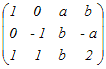 �̊K����
�̊K����

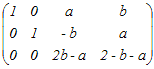

 , a
, a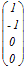 , a
, a , a
, a ,
,
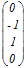 , a
, a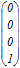
 �̊K���́C���̂ǂꂩ�D
�̊K���́C���̂ǂꂩ�D
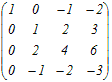
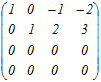
 �̊K����
�̊K����
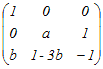

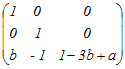
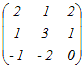 �ɂP��̍s��{�ό`���s���������ł͓����Ȃ��s��́C���̂ǂꂩ�D
�ɂP��̍s��{�ό`���s���������ł͓����Ȃ��s��́C���̂ǂꂩ�D