|
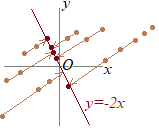
�i���̋��ނ̃��x��)
�@2010�N���݁C�u1���ϊ��v�͍��Z�̋��ȏ��ɂȂ��̂ŁC�����i�K�ł͂P���ϊ��̃C���[�W���S�����߂Ȃ����̂Ƃ��ċL�q �ʑ��C�ϊ��̒�`
�@�W��A�̊e�v�f���W��B�̗v�f�ɑΉ�������K����A����B�ւ��ʑ��Ƃ����D
�y�ϊ��̗�z�@�ʑ��̂������Ɍ��̏W���ƑΉ�������W���Ƃ�����ł�����̂��ϊ��Ƃ����D�i����W��A����W��A���g�ւ̎ʑ���ϊ��Ƃ����D�j �@�ϊ��̂����őΉ��̋K�����u�萔���̂Ȃ�1�����v�ŕ\�������̂��P���ϊ��Ƃ����D �@�m���ʏ�̓_�̈ړ� (x,y) �� (x’,y’)�n y’=x−y+3 �@���̂悤�Ȓ萔�����܂ޕϊ��̓A�t�B���ϊ��ƌĂ�C1���ϊ��ł͂Ȃ�. �@�m���ʏ�̓_�̈ړ� (x,y) �� (x’,y’)�n y’=x−y y’=x−y+2z z’=3x+y−2z 1���ϊ��̍s��
�@1���ϊ�y’=cx+dy �������� �́C�ϊ����̌W��a, b, c, d�������́C�s�� �Ō��܂�D�����ŁC���̍s����P���ϊ��̍s��Ƃ����D�i�R�����̂Ƃ������l�j
�s��̂����Z�ɂ��ẮC���̃y�[�W�Q��
�܂��C���͒���(x, y)�̂悤�ɍs�x�N�g���ŏ������_�̍��W�́C�s��v�Z�ł� |
|
(1.1)�@1���ϊ��ɂ��_�̑�
�@�^����ꂽ�P���ϊ��ɂ��_�̑������߂�ɂ��ϊ��̎� y’=cx+dy �ɓ_�̍��W(x, y)�������Čv�Z����悢�D �@�܂��́C�s��ŏ����ꂽ�ϊ��� �ɑ�����āC�s��̂����Z���s���悢�D
�y��1.1-1�z
�i�j�@1���ϊ� y’=x−4y �ɂ���āC�_(−2, 3)�͂ǂ̂悤�ȓ_�Ɉڂ���邩�D x’=2×(−2)+3×3=5 y’=(−2)−4×3=−14 (5, −14)…�i���j
�y��1.1-2�z
�i�j�@1���ϊ� �ɂ��_(3, 4)�̑������߂�D (2, 17)…�i���j
�y��1.1-3�z
�i�j�@1���ϊ� y’=2x+y+3z z’=4x−3y+2z �ɂ�_(1, −2, 3)�̑������߂�D x’=1+3×(−2)−3=−8 y’=2×1+(−2)+3×3=9 z’=4×1−3×(−2)+2×3=16 (8, 9, 16)…�i���j
�y��1.1-4�z
�i�j�@1���ϊ� �ɂ���āC�_(1, 0, 2)�͂ǂ̂悤�ȓ_�Ɉڂ���邩�D (8, −1, 5)…�i���j |
 1���ϊ�A�ɂ���ē_
1���ϊ�A�ɂ���ē_ 1���ϊ�A�ɂ���ăx�N�g��
1���ϊ�A�ɂ���ăx�N�g��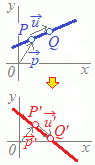 �i����j
�i����j (B)←
(B)←