ベクトル，行列の簡単な復習

== ベクトル，行列の簡単な復習 ==
（♪～超基本のレベル）【要約】

	例		例
1. ベクトル	行ベクトルの例 $\vec{a}=(3,4,-5)$ 列ベクトルの例 $\vec{b}=\begin{pmatrix} 2 \\ -3 \end{pmatrix}$	2. ベクトルの内積	$\vec{a}=(3,4),\vec{b}=(1,-2)$ のとき $\vec{a}\cdot \vec{b}=3\times 1+ 4\times (-2)=-5$ $\vec{c}=\begin{pmatrix} 3 \\ 4 \end{pmatrix}, \vec{d}=\begin{pmatrix} 2 \\ 1 \end{pmatrix}$ のとき $\vec{c}\cdot \vec{d}=3\times 2+ 4\times 1=10$
3. ベクトルの内積を Excelで計算する方法	=SUMPRODUCT(行, 行) または =SUMPRODUCT(列, 列)	4. 行列	3×2行列の例 $A=\begin{pmatrix} 1 & -3 \\ 5 & 4 \\ 2 & 0 \end{pmatrix}$ 2×3行列の例 $B=\begin{pmatrix} 1 & -3 & 0 \\ 5 & 4 & -1\end{pmatrix}$ 2次の正方行列の例 $C=\begin{pmatrix} 1 & -3 \\ 5 & 4 \end{pmatrix}$
5. 行列の積	$\begin{pmatrix}1 & 2 \\ 3 & 4 \end{pmatrix}$ $\begin{pmatrix}2\\ -1\end{pmatrix}$ $=\begin{pmatrix} 0 \\ 2 \end{pmatrix}$ $\begin{pmatrix}2 & -1 & 0 \\1 & 3 & -2\end{pmatrix}$ $\begin{pmatrix}1 & 6 \\3 & 4 \\5 & 2\end{pmatrix}$ $=\begin{pmatrix}-1 & 8 \\ 0 & 14\end{pmatrix}$	6. 行列の積を Excelで計算する方法	=MMULT(範囲1, 範囲2)

1. ≪ベクトル≫

※ベクトルは矢印を用いて図形的に表されることもあるが，この頁では成分で表すものだけを扱います．

○次の例のように，幾つかの数字を横に並べて，カンマで区切り，かっこでくくったものを行ベクトルといいます．高校で単にベクトルと言えば行ベクトルのことをいいます．
　単なる１つの変数ではなく，ベクトルであることを明示するために，変数名の上に矢印を付けて表します．

【例】
2次元行ベクトル（要素が2個のベクトル）の例
$\vec{a}=(3,4)$
3次元行ベクトル（要素が3個のベクトル）の例
$\vec{b}=(2,-3,5)$

※（注）
ベクトルを囲むかっこは，小かっこ (　　)を使わなければなりません．数学で，中かっこ {　　}を使うと，順序を問わずに中の要素が等しければよいということを表し，小かっこ (　　)を使うと順序まで指定したことになります．
【例】
　集合A={3, 4}は，要素が3と4とから成る集合で，これらがどの順に書かれているかを問わないから集合B={4, 3}に等しい．
　これに対して，ベクトル $\vec{a}=(3,4)$ はx=3，y=4という具合に書かれている順序を区別するので， $\vec{b}=(4,3)$ と $\vec{a}$ とは等しくない．
　このように，書かれている要素の順序を区別する場合には，小かっこ (　)で囲まなければなりません．

　行ベクトルをExcelなどのワークシート上で表すには，次の例のように第1の要素の左隣のセルを行見出し（行の表題）として［日本語でもよいが，これがベクトルの名前になる］として，セルに数字を並べます．（セルごとに区切られているので，区切り文字のカンマはいりません．もちろん，左端の行見出しに矢印は不要です．）

【例】
2次元行ベクトル（要素が2個のベクトル）の例

販売個数

3次元行ベクトル（要素が3個のベクトル）の例

月別の増減

−3

○次の例のように，幾つかの数字を縦に並べて，左右をかっこでくくったものを列ベクトルといいます．統計で単にベクトルと言えば列ベクトルを示すことが多い．

【例】
2次元列ベクトル（要素が2個のベクトル）の例
$\vec{a}=\begin{pmatrix} 3 \\ 4 \end{pmatrix}$
3次元列ベクトル（要素が3個のベクトル）の例
$\vec{b}=\begin{pmatrix} 2 \\ -3 \\ 5 \end{pmatrix}$

　行ベクトルをExcelなどのワークシート上で表すには，次の例のようにに第1の要素の上隣のセルを列見出し（列の表題）として［日本語でもよいが，これがベクトルの名前になる］として，セルに数字を並べます．（セルごとに区切られているので，区切り文字のカンマはいりません．もちろん，上端の列見出しに矢印は不要です．）

→右上に続く

【例】
2次元列ベクトル（要素が2個のベクトル）の例

販売個数

3次元列ベクトル（要素が3個のベクトル）の例

月別増減

−3

※教科書などでは，ベクトルを行ベクトルで表し，列ベクトルが必要な場合には，転置行列（行と列を入れ替えたもの）で表すことがある．これは，印刷物にするときに列ベクトルで書くと紙面に空白が多くできて経費が高くなり，見た目にも間延びして見えるからだと考えられる．

【例】
　行列 $A=\begin{pmatrix} 2 & 3 & 4 \\ 5 & 6 & 7 \end{pmatrix}$ の転置行列は $^t A=\begin{pmatrix} 2 & 5 \\ 3 & 6 \\ 4 & 7 \end{pmatrix}$

　行ベクトル $\vec{a}=(2,-3,5)$ の転置行列（行と列を入れ替えると列ベクトルになる）は $^t\vec{a}=\begin{pmatrix} 2 \\ -3 \\ 5 \end{pmatrix}$

　逆に，列ベクトルの転置行列は行ベクトルになるから，あるベクトルが $\vec{b}=\begin{pmatrix} 2 \\ -3 \\ 5 \end{pmatrix}$ となることを印刷物に書くときに
$^t \vec{b}=(2,-3,5)$
あるいは
$^t(2,-3,5)$
などと書かれることがある．

※これに対して，Excelのワークシートにおいては，横方向（行）の要素数は255個まで，縦方向（列）の要素数は数万個と列方向に多くのデータを入れることができるから，ベクトルは列ベクトルとして利用する方が有利になる．ちょっとしたアンケートを整理する場合でも，要素数が数百，数千となることは珍しくない．

2. ≪ベクトルの内積≫
○２つのベクトル $\vec{a}=(a_1,a_2)$ ， $\vec{b}=(b_1,b_2)$ の内積は
$\vec{a}\cdot \vec{b}=a_1 b_1 + a_2 b_2$
で定義されます．
　3次元ベクトル $\vec{a}=(a_1,a_2,a_3)$ ， $\vec{b}=(b_1,b_2,b_3)$ の内積は
$\vec{a}\cdot \vec{b}=a_1 b_1 + a_2 b_2 + a_3 b_3$
　ｎ次元ベクトル $\vec{a}=(a_1,a_2,a_3,...,a_n)$ ， $\vec{b}=(b_1,b_2,b_3,...,b_n)$ の内積は
$\vec{a}\cdot \vec{b}=a_1 b_1 + a_2 b_2 + a_3 b_3 + ... + a_n b_n$
※いずれの場合も，ベクトルの要素数（次元）が一致する場合にだけ内積が定義されます．要素数（次元）が異なるベクトル間には内積は定義されません．

〇列ベクトル相互についても同様です．すなわち
$\vec{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \\ ... \\ a_n \end{pmatrix}, \vec{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \\ ... \\ b_n \end{pmatrix}$ のとき
これらの内積は
$\vec{a}\cdot \vec{b}=a_1 b_1 + a_2 b_2 + a_3 b_3 + ... + a_n b_n$

【例】
$\vec{a}=(3,4),\vec{b}=(5,-1)$ のとき
$\vec{a}\cdot\vec{b}=3\cdot 5 + 4\cdot (-1)=11$
$\vec{p}=(2,5,4),\vec{b}=(3,-6,1)$ のとき
$\vec{p}\cdot\vec{q}=2\cdot 3 + 5\cdot (-6) + 4\cdot 1=-20$
$\vec{c}=\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \vec{d}=\begin{pmatrix} x \\ -x \\ 2x \end{pmatrix}$ のとき
$\vec{c}\cdot \vec{d}=x -2x + 6x=5x$

3. ≪ベクトルの内積をExcelで求める方法≫
　ベクトルの内積をExcelのワークシート上で求めるには，関数 =SUMPRODUCT() を使います．
　次の例のようにワークシート上に行と行で表される２つのベクトルの内積，または，列と列で表される２つのベクトルの内積を求めるには =SUMPRODUCT()･･･積の和･･･で計算できます．

【例】
　果物１個当たりの単価と購入個数が次のようになっているとき，

	A	B	C	D
1	くだもの	りんご	みかん	かき
2	単価	150	80	200
3	個数	3	4	2

これらの果物を購入した時の合計金額は
150×3+80×4+200×2=1170（円）
になります．
　りんごの単価（a1）にはりんごの個数（b1）を掛けます．みかん，かきについても同様です．このようにしてできた積を加えると合計金額になります．
　この計算をExcelのワークシート上で行うには，
=SUMPRODUCT(B2:D2, B3:D3)
とします．

※Excelでベクトルの演算を行うときは，行ベクトルの名前の文字列（左に付けた見出しのラベル）や列ベクトルの名前の文字列（上に付けた見出しのラベル）を含まない「正味のデータの範囲」を指定します．

→右上に続く

　くじの賞金とそれぞれの当たる確率が次のようになっているとき，

	A	B	C
1	くじ	賞金	確率
2	1等	1000	0.1
3	2等	500	0.2
4	3等	100	0.3
5	4等	0	0.4

このくじを１本引いたときにもらえる金額の期待値は
1000×0.1+500×0.2+100×0.3+0×0.4=230（円）
になります．
　この計算をExcelのワークシート上で行うには，
=SUMPRODUCT(B2:B5, C2:C5)
とします．

　りんご，みかん，かきの1個当たりの重さと購入個数とが次のようになっているとき，

	A	B	C
1	果物	重さ	個数
2	りんご	150	2
3	みかん	50	3
4	かき	100	4

これらの果物を購入したときの総重量は
150×2+50×3+100×4=850（g）
になります．
　この計算をExcelのワークシート上で行うには，
=SUMPRODUCT(B2:B4, C2:C4)
とします．

4. ≪行列≫
○数字を長方形に並べたものを行列といいます．

【例】
$\begin{pmatrix} 1 & -3 \\ 5 & 4 \end{pmatrix}$ ， $\begin{pmatrix} 0 & 2 & 5 \\ 0.3 & -0.1 & 0.2 \end{pmatrix}$ ， $\begin{pmatrix} 1 & 3 \\ 5 & 2 \\ 4 & 7 \end{pmatrix}$ ，
$\begin{pmatrix} 1 & -3 & 5 \end{pmatrix}$ ， $\begin{pmatrix} 2 \\ 3 \end{pmatrix}$ ， $\begin{pmatrix} 3 & 5 & 7 & -1 \end{pmatrix}$ ，

行列は小かっこ ( 　)で囲んで表し，要素の間に特にカンマなどは書きません．行列の要素を指定するには，横の並びを「行」とし，縦の並びを「列」として，その交差する場所をi行j列の成分という意味で(i, j)成分といいます．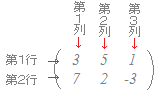

　右の行列では，(1, 2)成分は5で，(2, 1)成分は7です．
　この行列は２行と３列から成り立っており，２行３列の行列とか，2×3 行列と呼ばれます．

　１行から成る行列は行ベクトルと同じものになりますが，行列として表すときは要素の間のカンマを書きません．行ベクトルでは書きます．
　１列から成る行列は列ベクトルと同じです．

○行列はデータを整理するのに便利です．

個数	りんご	みかん	かき
A店	15	12	20
B店	12	13	15

--	重さ	価格
りんご	150	200
みかん	50	80
かき	100	250

→右上に続く

○行列の和は対応する成分の和を成分とする同じ型の行列で定義されます．

$A=\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{pmatrix}$ ， $B=\begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \end{pmatrix}$ のとき
$A + B=\begin{pmatrix} a_{11} + b_{11} & a_{12}+ b_{12} & a_{13}+ b_{13} \\ a_{21}+ b_{21} & a_{22} + b_{22} & a_{23} + b_{23} \end{pmatrix}$

【例】
$\begin{pmatrix} 15 & 12 & 20 \\ 12 & 13 & 15 \end{pmatrix}$ $+ \begin{pmatrix} 11 & 13 & 22 \\ 10 & 11 & 14 \end{pmatrix}$ $=\begin{pmatrix} 26 & 25 & 42 \\ 22 & 24 & 29 \end{pmatrix}$

次のようなデータがこの行列の和に対応するでしょう．

１月	りんご	みかん	かき
A店	15	12	20
B店	12	13	15

２月	りんご	みかん	かき
A店	11	13	22
B店	10	11	14

のとき，１月と２月の各店別，果物別売上高は

２月	りんご	みかん	かき
A店	26	25	42
B店	22	24	29

になります．

○同様にして，行列の差は対応する成分の差を成分とする同じ型の行列で定義されます．

$A=\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{pmatrix}$ ， $B=\begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \end{pmatrix}$ のとき
$A - B=\begin{pmatrix} a_{11} - b_{11} & a_{12}- b_{12} & a_{13}- b_{13} \\ a_{21}- b_{21} & a_{22} - b_{22} & a_{23} - b_{23} \end{pmatrix}$

【例】
$\begin{pmatrix} 15 & 12 & 20 \\ 12 & 13 & 15 \end{pmatrix}$ $- \begin{pmatrix} 11 & 13 & 22 \\ 10 & 11 & 14 \end{pmatrix}$ $=\begin{pmatrix} 4 & -1 & -2 \\ 2 & 2 & 1 \end{pmatrix}$

次のようなデータがこの行列の差に対応するでしょう．
今年度の８月と昨年度の８月の売れ行きが次の表のようになっているとき

今年	りんご	みかん	かき
A店	15	12	20
B店	12	13	15

昨年	りんご	みかん	かき
A店	11	13	22
B店	10	11	14

前年度と比較した場合の売れ行きの増加は

増加	りんご	みかん	かき
A店	4	−1	−2
B店	2	2	1

になります．（負の数は減少であることを示す）

→右上に続く

○行列の定数倍は対応する成分の定数倍を成分とする同じ型の行列で定義されます．

$A=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{pmatrix}$ のとき $kA =\begin{pmatrix} ka_{11} & ka_{12} \\ ka_{21} & ka_{22} \\ ka_{31} & ka_{32} \end{pmatrix}$

【例】
$2 \begin{pmatrix} 11 & 13 & 22 \\ 10 & 11 & 14 \end{pmatrix}$ $=\begin{pmatrix} 22 & 26 & 44 \\ 20 & 22 & 28 \end{pmatrix}$

次のようなデータがこの行列の定数倍に対応するでしょう．
今年度の８月と昨年度の８月の売れ行きが次の表のようになっているとき

今年 A	りんご	みかん	かき
A店	30	28	35
B店	23	24	27

昨年 B	りんご	みかん	かき
A店	11	13	22
B店	10	11	14

B店のかき以外は，今年度の売れ行きが昨年度の２倍以上であると言えます．

A	りんご	みかん	かき
A店	30	28	35
B店	23	24	27

2B	りんご	みかん	かき
A店	22	26	44
B店	20	22	28

○行列の積（掛け算）や行列の商（割り算）などの行列についての演算は，何でも定義できる訳ではありません．定義する場合は，後で役に立つ使い道があって他の性質と矛盾しないようなものでなければなりません．
　とりあえず第1段階としては，行列の積（掛け算）は以下に述べるように定義されますが，行列の商（割り算）は一般には定義されないということをしっかり押さえておく必要があります．

　混乱させるつもりはありまえんが，話だけ･･･大学レベルでもっと進んだ学習になれば，１種類の正方行列だけを扱っている式では，一般の数値と同様に和差積商の演算が自由にできるようになり，さらにもっと進んでeAのような「eの行列乗」でも自由に扱えるようになります．

5. ≪行列の積≫
　左の表はある人が甲店と乙店で購入した果物の個数，右の表は果物１個当たりの重量と価格の一覧表だとします．

	りんご	みかん	かき
甲店	1	2	3
乙店	4	5	6

	重量(g)	価格(円)
りんご	150	200
みかん	50	100
かき	100	150

　これらの表は，次のような行列に整理することができます．
$A=\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}$ ， $B=\begin{pmatrix} 150 & 200 \\ 50 & 100 \\ 100 & 150 \end{pmatrix}$

　この表を使って，甲店（左の行列の第1行目）で買ったくだものの総重量（右の行列の第1列目）を求めるには，表の中の次の部分だけを見て，背景色が同じ色の部分を掛け合わせてから足せばよい（積の和）

	りんご	みかん	かき
甲店	1	2	3

	重量(g)
りんご	150
みかん	50
かき	100

　すなわち，りんごの個数にはりんごの重量を，みかんの個数にはみかんの重量を，かきの個数にはかきの重量を掛けて足せばよい．
1×150+2×50+3×100=550(g)
になります．

（りんごの個数にみかんやかきの重量を掛けても意味がない．同様にして，みかんの個数にりんごやかきの重量を掛けても意味がなく，かきの個数にりんごやみかんの重量を掛けても意味がない）

　同様にして，乙店で買ったくだもの総価格を求めるには，表の中の次の部分だけを見て，背景色が同じ色の部分を掛け合わせてから足せばよい（積の和）
⇒乙店（左の行列の第2行目）で買ったくだものの総重量（右の行列の第1列目）を見る．

	りんご	みかん	かき
乙店	4	5	6

	重量(g)
りんご	150
みかん	50
かき	100

4×150+5×50+6×100=1450(g)
になります．

→右上に続く

　これらの結果は，2. ≪ベクトルの内積≫とよく似ていますが，次の点が違います．

(1) 左側は「行」として取り出し，右側は「列」として取り出しています．
(2) これら２つの"内積風"の計算は，行列で書くと次のようにまとめることができます．

	りんご	みかん	かき
甲店	1	2	3
乙店	4	5	6

	重量(g)
りんご	150
みかん	50
かき	100

	重量(g)
甲店	550
乙店	1450

　行列の記号で書けば
$\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}$ $\begin{pmatrix} 150 \\ 50 \\ 100 \end{pmatrix}$ $=\begin{pmatrix} 550 \\ 1450 \end{pmatrix}$ …(*)

　また，甲店、乙店で購入したそれぞれの価格は，次の行列で表すことができます．
$\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}$ $\begin{pmatrix} 200 \\ 100 \\ 150 \end{pmatrix}$ $=\begin{pmatrix} 850 \\ 2200 \end{pmatrix}$ …(**)

　さらに，これら(*)(**)の結果は，次のようにまとめることができます．
$\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}$ $\Bigl(\begin{matrix} 150 \\ 50 \\ 100 \end{matrix}$ $\begin{matrix} 200 \\ 100 \\ 150 \end{matrix}\Bigr)$ $=\Bigl( \begin{matrix} 550 \\ 1450 \end{matrix}$ $\begin{matrix} 850 \\ 2200 \end{matrix}\Bigr)$

このように，ｍ行とｎ列の積がｍｎ成分になると決めます．

ただし，そのそもこの行列の積が定義できるためには，りんご，みかん，かきで示したように，左から掛ける行列の「列数」と右から掛ける行列の「行数」が一致していなければなりません．
　そして，それらが一致しているときに，結果としてできる行列では，その仲介となっているりんご，みかん，かきは「消え」ます．

【要点】
○型が「しりとり」になっているときだけ積が定義できる．

○ｍ行とｎ列の積がｍ行ｎ列成分になる．
○積の行列の型は，左の行列の行数（ｍ）･･･行番号の最大値･･･と右の行列の列数（ｎ）･･･列番号の最大値･･･を見たら分かる．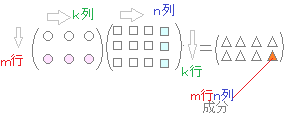

【例】
［2×2］型×［2×1］型→［2×1］型

$\begin{pmatrix} 1 & 2 \\ 3 & -4\end{pmatrix}$ $\begin{pmatrix} 5 \\ 6 \end{pmatrix}$ $=\begin{pmatrix} 17 \\ -9 \end{pmatrix}$

なお，左右の行列を入れ替えた次のような積は定義されない．［2×1］型×［2×2］型ではしりとりにならない．

$\begin{pmatrix} 5 \\ 6 \end{pmatrix}$ $\begin{pmatrix} 1 & 2 \\ 3 & -4\end{pmatrix}$

［3×3］型×［3×1］型→［3×1］型
$\begin{pmatrix} 1 & -4 & 0 \\ -2 & 5 & 1 \\ 3 & -6 & 0 \end{pmatrix}$ $\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}$ $=\begin{pmatrix} 1 \\ -1 \\ 3 \end{pmatrix}$

なお，左右の行列を入れ替えた次のような積は定義されない．［3×1］型×［3×3］型ではしりとりにならない．
$\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}$ $\begin{pmatrix} 1 & -4 & 0 \\ -2 & 5 & 1 \\ 3 & -6 & 0 \end{pmatrix}$

［1×2］型×［2×2］型→［1×2］型
$\begin{pmatrix} -1 & 2\end{pmatrix}$ $\begin{pmatrix} 3 & 4 \\ 5 & 6 \end{pmatrix}$ $=\begin{pmatrix} 7 & 8 \end{pmatrix}$

なお，左右の行列を入れ替えた次のような積は定義されない．［2×2］型×［1×2］型ではしりとりにならない．
$\begin{pmatrix} 3 & 4 \\ 5 & 6 \end{pmatrix}$ $\begin{pmatrix} -1 & 2 \end{pmatrix}$

［1×3］型×［3×2］型→［1×2］型
$\begin{pmatrix} 1 & 2 & 3 \end{pmatrix}$ $\begin{pmatrix} 1 & 0 \\ 1 & 1 \\0 & 1 \end{pmatrix}$ $=\begin{pmatrix} 3 & 5 \end{pmatrix}$

この場合も，左右の行列を入れ替えたときの行列の積は定義されない．

［2×3］型×［3×2］型→［2×2］型
$\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}$ $\begin{pmatrix} 1 & 0 \\ 0 & 4 \\ 2 & 0 \end{pmatrix}$ $=\begin{pmatrix} 7 & 8 \\ 16 & 20\end{pmatrix}$

この場合，左右の行列を入れ替えたときの行列の積は［3×3］型になる．
$\begin{pmatrix} 1 & 0 \\ 0 & 4 \\ 2 & 0 \end{pmatrix}$ $\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}$ $=\begin{pmatrix} 1 & 2 & 3 \\ 16 & 20 & 24 \\ 2 & 4 & 6\end{pmatrix}$

［3×2］型×［2×4］型→［3×4］型
$\begin{pmatrix} 1 & 0 \\ 0 & -2 \\ 2 & 4 \end{pmatrix}$ $\begin{pmatrix} 0 & 4 & 0 & 8 \\ -3 & 0 & 7 & 0 \end{pmatrix}$ $=\begin{pmatrix} 0 & 4 & 0 & 8 \\ 6 & 0 & -14 & 0 \\ -12 & 8 & 28 & 16\end{pmatrix}$

この場合も，左右の行列を入れ替えたときの行列の積は定義されない．

6. ≪行列の積をExcelで計算する方法≫
　次の表のように，［4×3］型の行列がA1:C4の範囲に書き込まれていて，［3×2］型の行列がD1:E3の範囲に書き込まれているとき，

	A	B	C	D	E	F	G
1	-3	0	-1	1	0	-7	1
2	0	1	2	2	2	10	0
3	-1	2	-3	4	-1	-9	7
4	0	1	-1			-2	3

これら２つの行列の積
$\begin{pmatrix} -3 & 0 & -1 \\ 0 & 1 & 2 \\ -1 & 2 & 3 \\ 0 & 1 & -1 \end{pmatrix}$ $\begin{pmatrix} 1 & 0 \\ 2 & 2 \\ 4 & -1 \end{pmatrix}$
の結果をExcelで計算して，図のようにF1:G4の範囲に書き込むには．

(1) セルF1に =MMULT(A1:C4, D1:E3) と書き込む．
　このとき，結果の行列のすべての要素が書き込まれるのではなく，その内の1行１列成分(−7)だけが書き込まれる．
(2) F1をコピー&ペーストなどしても行列の成分は書き込まれない．Excelのワークシート上で，求める範囲を「配列」として指定すると他の要素も書き込まれる．
　i) 解答とすべき範囲（F1からG4までの長方形）をマウスでドラッグして反転表示にする．
　ii) マウスをExcel画面の上の方にある数式バーと呼ばれる部分（fxの右側の窓）に当てる．
　iii) Ctrl+Shift+Enter（CtrlキーとShiftキーを押している間にEnterキーを押す=３本の指を使う）

※i) において結果を表す範囲を間違って反転させている場合，それが実際よりも狭い範囲を選んでいるときは選んだ範囲の要素だけが書き込まれます．実際の範囲よりも大きな範囲を選んでいるときは，そのはみ出した範囲は #NA（Not A Value=数値ではない）と表示されます．

　1行と１列のようにベクトル，行列のどちらにでも解釈できそうな場合の見分け方

	A	B	C	D	E	F	G
1	-3	0	-1	1	0	-7	1
2	0	1	2	2	2	10	0
3	-1	2	-3	4	-1	-9	7
4	0	1	-1			-2	3

　図で緑の背景色で示した行ベクトル（A1:B1）と行ベクトル（A3:B3）の内積を求めるときは，
=SUMPRODUCT(A1:B1, A3:B3)
　図で茶色の背景色で示した列ベクトル（D1:D2）と列ベクトル（F1:F2）の内積を求めるときも，
=SUMPRODUCT(D1:D2, F1:F2)

横横，縦縦は=SUMPRODUCT()

　図で緑の背景色で示した行ベクトル（A1:B1）と列ベクトル（F1:F2）の積を求めるときは，
=MMULT(A1:B1, F1:F2)

横×縦は=MMULT()

..高卒～大学数学のメニューに戻る　メニューに戻る