|
(2) 成分による定義
2つのn次元ベクトルこの定義は,シグマ記号を用いて次のように書いてもよい
【例1.2.1】
2次元ベクトル
【例1.2.2】
3次元ベクトル |
【例1.2.3】
4次元ベクトル
※ベクトルの内積は,スカラー積とも呼ばれ,2つのベクトルの積が単なる1つの数(スカラー)になります.すなわち,ベクトルの内積はベクトルにならないことに注意
例えば,上の【例2.1】では,2次元×2の合計4個の成分 【例2.2】では,3次元×2の合計6個の成分 【例2.3】では,4次元×2の合計8個の成分 |
|
(3) ベクトル内積の性質
ベクトルの内積は次の性質を満たす.ⅰ) [対称性] ⅱ) [双線形性] 第1変数について線形 第2変数について線形 ⅲ) [正定値性] (等号成立は |
(解説) これらの性質は,ベクトルの成分による定義を用いれば簡単に示すことができる. ⅰ)← ⅱ)以下も同様にして示される ⅲ) に関連して,ベクトルの大きさ(長さ,絶対値,ノルム) |
|
(2) 成分による定義
(解説) ※これは定義であるから,証明する必要はないが,定義自体が覚えにくいので,基本ベクトルと結びつけると楽に理解できる
そこで,展開公式 および
※この展開公式が成立することは,後で示す.
|
行列式が使える人は,次の形で覚えてもよい.
【例2.2.1】
1) 1) 2) 2) |
|
(3) ベクトル外積の性質
ベクトルの外積は次の性質を満たす.ⅰ) ⅱ) ⅲ) kが実数のとき ⅳ) 内積 |
ⅴ)内積 ⅵ) 内積 ⅶ) |
|
(解説) ⅰ)← 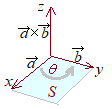 図による定義から解説すれば,
図による定義から解説すれば,次に,ベクトルの大きさは,2つのベクトル したがって, |
成分による定義から解説すれば, 行列式で覚える方法から解説すれば, において,2行目と3行目を入れ換えると,符号だけ逆になるから |
|
ⅱ)← 成分を用いて示すと(これを目で追うのはかなりの苦痛!) |
行列式で覚える方法から解説すれば, において,行列式の値は各行について線形(特に,今の場合は3行目について線形)だから 後半の式も同様にして示される |
|
ⅲ)← 図でも,成分でもほとんど明らかであるから,証明は略する ⅳ)← ⅴ)← 次の行列式を考える 1行目に沿って展開すると これは, 2行目に沿って展開すると これは, 同様にして,3行目に沿って展開すると, 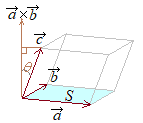 ※この行列式
※この行列式は,絶対値をとって符号を正にすれば,3つのベクトル なぜなら, |
スカラーとベクトルの外積 同様にして, このとき, が成り立つ.すなわち,変数(ベクトル
(証明)
そこで,これ(ら)を単にサイクリックな順
(証明)
2つのベクトルの内積は変数(ベクトル)の順序を入れ替えても変わらないから, 同様にして 2つのベクトルの外積は変数(ベクトル)の順序を入れ替えると符号が逆になるから, 同様にして 同様にして ※ |
ⅵ)←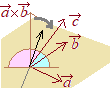 成分計算を行えば示せるが,とても長い計算になるので,ここでは図で考えてみる.
成分計算を行えば示せるが,とても長い計算になるので,ここでは図で考えてみる.まず 次に, と書ける. さらに,このベクトルは したがって, すなわち の形に書けるので,後は必要条件を使ってtの値が1になることを示せばよい. 右辺は, よって,t=1が必要条件になることが示された. |
特別な値として
なお, さらに, の符号が納得できる. を使えば,別途証明しなくて済む ⅶ)← |
|
【例2.3.1】
(証明)ベクトルの外積について,ヤコビの恒等式 が成り立つことを示してください. ⅳ)の公式により 右辺の和は が成り立つ
【例2.3.2】
(証明)であるならば, ⅵ) 内積 だから ならば 同様にして, |
例えば, 他方で となって, このとき,
【例2.3.3】
(証明)3次元ベクトル は,ベクトル ⅵ) 内積 において, 移項すると ここで, 両辺を が得られる. |