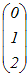|
■ベクトルの直交条件
○ベクトルの内積
２つのベクトル=(x1 , y1 , z1 , ...) , =(x2 , y2 , z2 , ...) について，内積·は x1x2+y1y2+z1z2+... になります．
【例１】
=(1, 2, 3), =(6, −5, 4)のとき ·=1·6+2·(−5)+3·4=8 ○ベクトルの直交条件 ２つのベクトル , が直交する（垂直になる）ための条件は ·=0 すなわち x1x2+y1y2+z1z2+...=0
【例２】
=(x, 2, 4), =(1, −3, 2)のとき ベクトル , が直交する（垂直になる）ための条件は ·=x−6+8=0 すなわちx=−2となります．
≪参考≫
ベクトルの内積を図形的に解釈すると， ·=||||cosθ になります． 他方で，ベクトルの内積を数式的に解釈すると，（３次元，４次元，５次元，...であっても） ·=x1x2+y1y2+z1z2+... になります． そこで，でない２つのベクトルが
「直交する」⇔「なす角がθ=90°」⇔「cos90°=0」
となります．
⇔「·=||||cosθ=0」 ⇔「x1x2+y1y2+z1z2+...=0」
平成16年度技術士第一次試験問題［共通問題］
【数学】Ⅲ-15 ３次元空間の２つのベクトル(1, −2, 3),(3, −2, 1)の両方に垂直な単位ベクトルで，成分がすべて正のものは次のどれか． 1(, , ) 2(, , ) 3(, , ) 4(, , ) 5(, , ) 解説 
求める単位ベクトルを(x, y, z)とおくと単位ベクトルだから x2+y2+z2=1…(1) (1, −2, 3)に垂直だから x−2y+3z=0…(2) (3, −2, 1)に垂直だから 3x−2y+z=0…(3) (3)−(2) 2x−2z=0 x=z…(4) これを(3)に代入 3z−2y+z=0 y=2z…(5) (4)(5)よりx=t, y=2t, z=tとおける これを(1)に代入 t2+4t2+t2=1 6t2=1 t=± x, y, z>0によりt>0だから t= したがって x=, y=, z= → 2 |
○この頁に登場する【問題】は，公益社団法人日本技術士会のホームページに掲載されている「技術士第一次試験過去問題 共通科目A 数学」の引用です．（=公表された著作物の引用）
○【解説】は個人の試案ですが，Ｗｅｂ教材化にあたって「問題の転記ミス」「考え方の間違い」「プログラムの作動ミス」などが含まれる場合があり得ます． 問題や解説についての質問等は，原著作者を煩わせることなく，当Ｗｅｂ教材の作成者（<浅尾>）に対して行ってください．
平成17年度技術士第一次試験問題［共通問題］
【数学】Ⅲ-12 4次元空間の２つのベクトル =(1, 0, −1, 1), =(0, −2, −t, 0) に対して，2+と−2+が垂直であるとき，正の数tの値は，次のどれか． 11 22 33 48 55 解説
2+=2(1, 0, −1, 1)+(0, −2, −t, 0)
=(2, 0, −2, 2)+(0, −2, −t, 0) =(2, −2, −t−2, 2) −2+=−2(1, 0, −1, 1)+(0, −2, −t, 0) =(−2, 0, 2, −2)+(0, −2, −t, 0) =(−2, −2, −t+2, −2) 2+⊥−2+だから 2·(−2)+(−2)·(−2)+(−t−2)·(−t+2)+2·(−2)=0 −4+4+t2−4−4=0 t2=±2 t>0によりt=2 → 2 |
|
平成18年度技術士第一次試験問題［共通問題］
【数学】Ⅲ-12 ３つのベクトルa=(a, 1, 1), b=(0, 1, b), c=(1, 1, c)が互いに垂直であるとき，aの値は次のどれか． 1−2 2−1 30 41 52 解説
a⊥bだから
a·0+1·1+1·b=0 ⇔ 1+b=0…(1) b⊥cだから 0·1+1·1+b·c=0 ⇔ 1+bc=0…(2) c⊥aだから 1·a+1·1+c·1=0 ⇔ a+1+c=0…(3) (1)からb=−1 これを(2)に代入：c=1 これを(3)に代入：a=−2 → 1 |
a+tb=
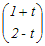 とa= が垂直だから1(1+t)+2(2−t)=0 5−t=0 t=5 → 5 |
|
求めるベクトルを
 とおく−x+y+2z=0 2x+2y−z=0 x,yについてとき，zについては解かないことにして，見やすくするために（ ）に入れると −x+y=(−2z)…(1) 2x+2y=(z)…(2) (2)−(1)×2 4x−5z=0 x=(z) これを(1)に代入 −z+y+2z=0 y=(−z) z=tとおくと x=(t), y=(−t), z=(t) t=−4のとき x=−5, y=3, z=−4 → 4 |
平成23年度技術士第一次試験問題［共通問題］
【数学】Ⅲ-13 ２つのベクトルa=(−3, 4, 1), b=(−1, 2, k)に対し，a−bとbが直交するとき，kの値は次のどれか． 11,−3 2−1,3 3−2,3 4−2,2 5−3,3 解説
a−b=(−3, 4, 1)−(−1, 2, k)=(−2, 2, 1−k)とb=(−1, 2, k)が直交するのだから
(−2)·(−1)+2·2+(1−k)·k=0 2+4+k−k2=0 k2−k−6=0 (k+2)(k−3)=0 k=−2, 3 → 3 |
|
sa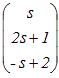+b=
 ，a+tb=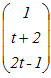 が直交するのだからs·1+(2s+1)·(t+2)+(−s+2)·(2t−1)=0 s+2st+4s+t+2−2st+s+4t−2=0 6s+5t=0 → 5 |
，
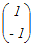
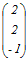の両方に垂直なベクトルは，次のどれか．
, b=
..高卒～大学数学のメニューに戻る
○===メニューに戻る