【回転体の体積】
　y=f(x) (a≦x≦b)とx軸とで囲まれる図形をx軸のまわりに回転して得られる回転体の体積Vは
V=π f(x)2dx で求められます．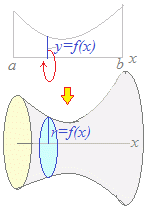

　上の図のようにx軸のまわりに回転させたとき，x軸に垂直に切った断面は円になり，その半径はf(x)になります．
　したがって，断面積はS(x)=πf(x)2になり，これをa≦x≦bの区間で積分すれば，回転体の体積になります．

○この頁に登場する【問題】は，公益社団法人日本技術士会のホームページに掲載されている「技術士第一次試験過去問題 共通科目A 数学」の引用です．（=公表された著作物の引用）

○【解説】は個人の試案ですが，Ｗｅｂ教材化にあたって「問題の転記ミス」「考え方の間違い」「プログラムの作動ミス」などが含まれる場合があり得ます．
　問題や解説についての質問等は，原著作者を煩わせることなく，当Ｗｅｂ教材の作成者（<浅尾>）に対して行ってください．

平成16年度技術士第一次試験問題［共通問題］
【数学】�V-8
　曲線y=とx軸およびx=1とで囲まれた部分を，x軸の周りに回転させて得られる回転体の体積は，次のどれか． 1π 2 3 4 5
解説

V=π ()2dx=π x3dx=π =π(−0)= → 4

平成19年度技術士第一次試験問題［共通問題］
【数学】�V-6
　曲線y=cos x (−≦x≦)とx軸とで囲まれた部分を，
x軸の周りに回転させて得られる回転体の体積は，次のどれか． 1 2 3 4 5 解説

V=πcos2x dx=πdx=π+

=π{(0+)−(0−)}= → 5

平成23年度技術士第一次試験問題［共通問題］
【数学】�V-8
　曲線y=cos−1xとx軸およびy軸とで囲まれた部分をy軸の周りに回転させて得られる回転体の体積は，次のどれか． 1 2π 3 42π 5
解説

逆三角関数
y=cos−1x ⇔ x=cos y
は，右図のように
−1≦x≦1, 0≦y≦π
の区間で定義されます．
この区間において，x軸およびy軸とで囲まれるのは，0≦y≦の部分です．
V=π x2 dy←yで積分
=π cos2y dy

=π dy

=π +

=π{(0+)−(0+0)}= → 5