|
【この頁で引用している問題の出典】
(出典A) 「微分積分学Ⅱ」(共立出版 基礎数学講座7巻/宇野利雄著) (出典B) 「新編 高専の数学3 問題集」(森北出版/田代嘉宏著) (出典C) 「理工系基礎 微分積分学」(培風館/堀内龍太郎.川崎廣吉.浦部治一郎共著) (出典D) 「数学へのアプローチ」(裳華房/八木克已著)
【記号】
○ 領域D:*1≦x≦*2, *3≦y≦*4における重積分 f(x,y)dxdy (*1, *2は定数である場合も,yに依存する場合もある.同様に,*3, *4は定数である場合も,xに依存する場合もある.)
を,まずxについて積分してから,次にyについて積分を行う累次積分(繰り返し積分)として行うことを
( f(x,y)dx)dy …(1)
で表す.(1)式は dy f(x,y)dx …(1’) という記号で表されることもある.この場合において,xについて積分した結果は,一般にはyを含んだ式となっているので, dy の部分は,そのyを含んだ関数の積分という意味になる. ○ 同様にして, dx f(x,y)dy …(2’) は,まずyについて積分して得られる(一般にはxを含んだ関数になる)ものを,次にxで積分したもの ( f(x,y)dy)dx …(2) を表す.
例1(2xydy)dxの積分の順序を換えると
(2xydx)dyになる 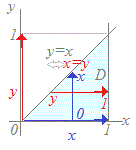 ≪解説≫
≪解説≫右図の領域Dにおいて, (1) 青の縦線で示した線に沿って,はじめにxを固定して,それぞれのxに対して,0≦y≦xの区間で変数yで積分してxを含んだ関数として得られる式が 2xydy (2) 次に,0≦x≦1の区間で変数xで積分するというのが元の式 (2xydy)dx が表しているもの.
2xydy=xy2=x3
積分の順序を変更して,はじめにyを固定して,それぞれのyに対して,xで積分するときは,図のように積分区間の左端がy,右端が1になる.x3dx=x4= になる (1) 赤の横線で示した線に沿って,y≦x≦1の区間で変数xで積分して得られる式は 2xydx (2) これらを0≦y≦1の区間で変数yで積分すると (2xydx)dy
2xydy=x2y=y−y3
(y−y3)dy=y2−y4=−= になる
例2dyf(x,y)dxの積分の順序を換えると
dx f(x,y)dyになる 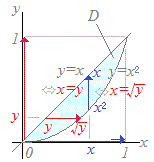 ≪解説≫
≪解説≫右図の領域Dにおいて, (1) 赤の横線に沿って,はじめにyを固定して,それぞれのyに対して,y≦x≦の区間で変数xで積分してyを含んだ関数として得られる式が f(x,y)dx (2) 次に,0≦y≦1の区間で変数yで積分するというのが元の式 dyf(x,y)dx が表しているもの. 積分の順序を変更して, (1) はじめにxを固定して,それぞれのxに対して,yで積分するときは,青の縦線に沿って,x2≦y≦xの区間で変数yで積分して得られる式が f(x,y)dy (2) これらを0≦x≦1の区間で変数xで積分すると dx f(x,y)dy
例3dx2x2ydyの積分の順序を換えると
2x2ydxdy+2x2ydxdyになる (出典B)
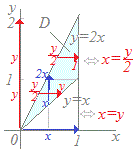 ≪解説≫
≪解説≫右図の領域Dにおいて, (1) 青の縦線で示した線に沿って,はじめにxを固定して,それぞれのxに対して,x≦y≦2xの区間で変数yで積分してxを含んだ関数として得られる式が 2x2ydy (2) 次に,0≦x≦1の区間で変数xで積分するというのが元の式 dx2x2ydy が表しているもの. 積分の順序を変更して,はじめにyを固定して,それぞれのyに対して,xで積分するときは,図のように積分区間の右端がyの値によって変わるので,2つの領域に分けて求める. (1) 0≦y≦1の区間では,赤の線で示した線に沿って,≦x≦yの区間で変数xで積分して得られる式は 2x2ydx 1≦y≦2の区間では,赤の線で示した線に沿って,≦x≦1の区間で変数xで積分して得られる式は 2x2ydx (2) これらを0≦y≦2の区間で変数yで積分すると 2x2ydxdy+2x2ydxdyになる ※(参考)どちらで計算しても,結果はになる |
 右図の領域
右図の領域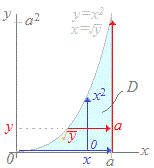 右図の領域
右図の領域 右図の領域
右図の領域 右図の領域
右図の領域