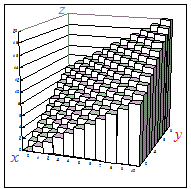
○図１のような立体の体積（縦棒の体積の総和）は，面積要素ds=dxdyに高さz=f(x, y)を掛けて得られる体積要素
dV=f(x, y)ds=f(x, y)dxdy
の総和として，定義域D上の重積分 .f(x, y)dxdy
で求めることができます．
○f(x, y)が連続関数で，各変数の定義域がa≦x≦b, α≦y≦βであるとき,この重積分は . f(x, y)dx dy…(1)
または . f(x, y)dy dx…(2)
のように，１変数の積分の繰り返しによって行うことができます．
　(1)は図２のように，まず変数yを固定して，各々のyについて，xで積分し（図で示した壁の面積S(y)を求めて），次にyの関数として表されたその面積をyで積分することによって体積を求めることに対応しています．
　(2)は図３のように，初めにxを固定してyで積分し，図で示した壁の面積S(x)を求めて，次にxで積分するものです．
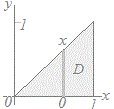○変数の定義域が0≦x≦1, 0≦y≦xのように他の変数に依存しているときは . f(x, y)dy dx

または0≦y≦1, y≦x≦1として
. f(x, y)dx dy
のように計算できます．

○この頁に登場する【問題】は，公益社団法人日本技術士会のホームページに掲載されている「技術士第一次試験過去問題 共通科目A 数学」の引用です．（=公表された著作物の引用）

○【解説】は個人の試案ですが，Ｗｅｂ教材化にあたって「問題の転記ミス」「考え方の間違い」「プログラムの作動ミス」などが含まれる場合があり得ます．
　問題や解説についての質問等は，原著作者を煩わせることなく，当Ｗｅｂ教材の作成者（<浅尾>）に対して行ってください．

平成16年度技術士第一次試験問題［共通問題］
【数学】�V-12
　閉領域D:0≦x≦1, 0≦y≦xに対して，
.(x+ay)dxdy=1
となるとき，定数aの値は次のどれか．
10 21 32 43 54
解説

まず，yについて積分してから，次にxについて積分すると (x+ay)dxdy= (x+ay)dy dx
(x+ay)dy=xy+y2 =x2+x2=x2
(x+ay)dy dx=x2dx
= ===1となるから
a+2=6
a=4 → 5
※　この問題で，変数x→yの順に積分すると，計算がやや長くなる
0≦x≦1, 0≦y≦x→y≦x≦1, 0≦y≦1と読み替える
(x+ay)dxdy= (x+ay)dx dy
(x+ay)dx=...=+ay−y2
(+ay−y2)dy=...==1
よりa=4

平成17年度技術士第一次試験問題［共通問題］
【数学】�V-10
　閉領域D:0≦x≦1, x≦y≦1に対して，
重積分x2y dxdyの値は次のどれか．
1 2 3 4 5 解説

まず，yについて積分してから，次にxについて積分すると x2y dxdy= x2y dy dx
x2y dy=x2y2 =−
(−)dx=− =−= → 1
※（別解）
0≦x≦y≦1→0≦x≦y, 0≦y≦1と読み替える
x2y dx=x3y =
dy=y5 =

平成18年度技術士第一次試験問題［共通問題］
【数学】�V-10
　 重積分e−x+ydxdyの値は，次のどれか．ただし，
D:0≦y≦x≦1とし，eは自然対数の底とする．
1e−2 2e−1 3e−1 4e 5e+1
解説

0≦y≦x≦1 → 0≦y≦xかつ0≦x≦1
まず，0≦y≦xの区間についてyについて積分してから，次に0≦x≦1の区間についてxについて積分すると
e−x+ydxdy= e−x+ydy dx
e−x+ydy=e−x+y =1−e−x
(1−e−x)dx=x+e−x =(1+e−1)−(0+1)=e−1 → 3
（別解）
0≦y≦x≦1 → y≦x≦1かつ0≦y≦1
まず，y≦x≦1の区間についてxについて積分してから，次に0≦y≦1の区間についてyについて積分すると
e−x+ydxdy= e−x+ydx dy
e−x+ydx=−e−x+y =(−e−1+y)−(−e0)=1−ey−1
(1−ey−1)dy=y−ey−1 =(1−1)−(0−e−1)=e−1 → 3

平成19年度技術士第一次試験問題［共通問題］
【数学】�V-11
　重積分sinx cosy dxdyの値は，次のどれか．ただし，
D:0≦x≦, 0≦y≦とする．
1 2 3 4 5
解説

sin x cos y dxdy= sin x cos y dx dy
sin x cos y dx=−cos x cos y=cos y
cos y dy=sin y= → 2

平成20年度技術士第一次試験問題［共通問題］
【数学】�V-11
　D : 0≦x≦π, 0≦y≦1のとき，
重積分xcosxy dxdyの値は次のどれか．
1 2 3 41 52
解説

x cos xy dxdy= x cos xy dy dx
x cos xy dy=sin xy=sin x
sin x dx=−cos x=(−(−1))−(−1)=1+1=2 → 5

平成21年度技術士第一次試験問題［共通問題］
【数学】�V-10
重積分(x−y)2 dxdyの値は，次のどれか．
ただし，D : x≧0, y≧0, x+y≦1とする．
1 2 3 4 51
解説

x≧0, y≧0, x+y≦1 → 0≦y≦1−x, 0≦x≦1とする
(x−y)2 dxdy= (y−x)2 dy dx
(x−y)2 dy=(y−x)3={ (1−2x)3+x3}
{(1−2x)3+x3}dx=(1−2x)4+

={(−+)−(−)}= → 1

平成22年度技術士第一次試験問題［共通問題］
【数学】�V-10
定数a, bに対して，(ax+by)dxdy=1とする．
このとき，a+bの値は，次のどれか．ただし，D : 0≦x≦1, 0≦y≦1とする．
10 2 31 4 52
解説

(ax+by)dxdy= (ax+by)dy dx
(ax+by)dy=axy+y2=ax+y2
(ax+y2)dx=x2+x

=+=1 より
a+b=2 → 5

平成23年度技術士第一次試験問題［共通問題］
【数学】�V-10
重積分(x+y)2 dxdyの値は，次のどれか．
ただし，D : 0≦x≦1, 0≦y≦1とする．
1 2 3 41 5
解説

(x+y)2 dxdy= (x+y)2 dx dy
(x+y)2 dx=(x+y)3={ (1+y)3−y3}
{(1+y)3−y3}dy=(1+y)4−y4

={16−1)−(1−0)}= → 5

平成24年度技術士第一次試験問題［共通問題］
【数学】�V-10
重積分(x+2y)dxdyの値は，次のどれか．
ただし，D : 1≦x≦3, 2≦y≦3とする．
110 211 312 413 514
解説

(x+2y)dxdy= (x+2y)dx dy
(x+2y)dx=x2+2xy=(+6y)−(+2y)

=4+4y
(4+4y)dy=4y+2y2

=(12+18)−(8+8)=14 → 5

H24の�V-10の問題いいですね。
＝＞［作者］：連絡ありがとう．