|
底aが a>1のとき
logax>logat → x>t
(解説)底aが 0<a<1のとき logax>logat → x<t 図1に示されるように, 底aがa>1のとき,グラフは単調増加関数(右上がりのグラフ)だから, logax>logatならば,x>tが成り立ちます. 底aが0<a<1のとき,グラフは単調減少関数(右下がりのグラフ)だから, logax>logatならば,x<tが成り立ちます.
注意
0<a<1のとき,対数を外したとき不等号の向きが逆になります. |
図1
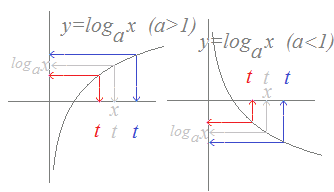
対数方程式の場合と同様に, 真数は正の数でなければなりません.
この真数条件は元の不等式で確かめる必要があり,元の不等式を変形したものでは一般に条件が変わってしまいます. |
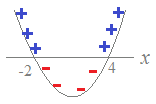 2次不等式を因数分解で解くと
2次不等式を因数分解で解くと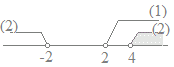 (1)(2)→
(1)(2)→ 2次不等式を因数分解で解くと
2次不等式を因数分解で解くと (1)(2)→
(1)(2)→