== 対数関数のグラフ ==
≪要点≫
(A) y=axのグラフを対称移動して y=logaxのグラフを作る方法
対数の形で書かれる式 y=logaxは,指数の形で書かれる式 y=axの x座標と y座標の役割を入れ替えたものです.
(ただし, a>0, a≠1, x>0の範囲で考えます)
y=ax
 ( xと yを入れ替える)
y=logax
◎x座標とy座標を入れ替えると,「縦のもの」と「横のもの」が入れ替わります.
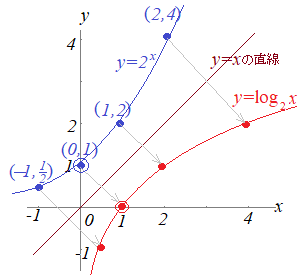
◎対数関数のグラフy=logaxのグラフは,指数関数のグラフy=axをy=xの直線に関して対称移動したものになります.
【例1】
| y=2x |  \( \frac{1}{2}=2^{-1} \) \( \frac{1}{2}=2^{-1} \) | 1=20 | 2=21 | 4=22 |
| (x, y) | ) \( (-1,\hspace{2px}\frac{1}{2})\) \( (-1,\hspace{2px}\frac{1}{2})\) | (0, 1) | (1, 2) | (2, 4) |

| y=log2x |  \( -1=\log_2 \frac{1}{2} \) \( -1=\log_2 \frac{1}{2} \) | 0=log21 | 1=log22 | 2=log24 |
| (x, y) | ) \( (\frac{1}{2},\hspace{2px}-1) \) \( (\frac{1}{2},\hspace{2px}-1) \) | (1, 0) | (2, 1) | (4, 2) |
【重要】
1. 指数関数の定義域: −∞<x<∞, 値域: 0<y<∞

対数関数の定義域:0<x<∞, 値域:−∞<y<∞
2. 指数関数のグラフは常に点 (0, 1)を通る

対数関数のグラフは常に点(1, 0)を通る
3. 各々の a (>0)について,指数関数のグラフは点 (1, a)を通る

各々のa (>0)について,対数関数のグラフは点(a, 1)を通る
4. 指数関数のグラフは,x軸を漸近線とする

対数関数のグラフはy軸を漸近線とする
5. y=axの aを指数関数の底(てい : base)という.
(1) 底 a>1のとき,指数関数 y=axは単調増加関数になる.

a>1のとき,対数関数y=logaxは単調増加関数になる
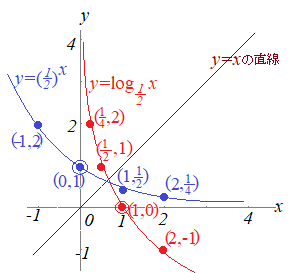
【例2】
^x) \( y=(\frac{1}{2})^x \) \( y=(\frac{1}{2})^x \) | ^{-1}) \( 2=(\frac{1}{2})^{-1} \) \( 2=(\frac{1}{2})^{-1} \) | ^{0}) \( 1=(\frac{1}{2})^{0} \) \( 1=(\frac{1}{2})^{0} \) | ^{1}) \( \frac{1}{2}=(\frac{1}{2})^{1} \) \( \frac{1}{2}=(\frac{1}{2})^{1} \) | ^{2}) \( \frac{1}{4}=(\frac{1}{2})^{2} \) \( \frac{1}{4}=(\frac{1}{2})^{2} \) |
| (x, y) | ) \( (-1,\hspace{2px}2) \) \( (-1,\hspace{2px}2) \) | (0, 1) | ) \( (1,\hspace{2px}\frac{1}{2}) \) \( (1,\hspace{2px}\frac{1}{2}) \) | ) \( (2,\hspace{2px}\frac{1}{4}) \) \( (2,\hspace{2px}\frac{1}{4}) \) |

 \( y\!=\!\log_{\frac{1}{2}}x \) \( y\!=\!\log_{\frac{1}{2}}x \) |  \( -1\!=\!\log_{\frac{1}{2}}2 \) \( -1\!=\!\log_{\frac{1}{2}}2 \) |  \( 0\!=\!\log_{\frac{1}{2}}1 \) \( 0\!=\!\log_{\frac{1}{2}}1 \) |  \( 1\!=\!\log_{\frac{1}{2}}\frac{1}{2} \) \( 1\!=\!\log_{\frac{1}{2}}\frac{1}{2} \) |  \( 2\!=\!\log_{\frac{1}{2}}\frac{1}{4} \) \( 2\!=\!\log_{\frac{1}{2}}\frac{1}{4} \) |
| (x, y) | ) \( (2,\hspace{2px}-1) \) \( (2,\hspace{2px}-1) \) | (1, 0) | ) \( (\frac{1}{2},\hspace{2px}1) \) \( (\frac{1}{2},\hspace{2px}1) \) | ) \( (\frac{1}{4},\hspace{2px}2) \) \( (\frac{1}{4},\hspace{2px}2) \) |
【重要】
1.〜4.までは,【例1】と全く同じ
5.の次の点だけが異なる
(2) 底a<1のとき,指数関数y=axは単調減少関数になる.
|
 (xとyを入れ替える)
(xとyを入れ替える)








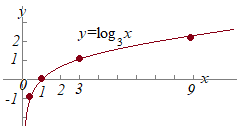
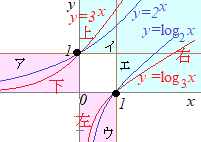

 1. 底が1よりも大きな異なる数のとき,
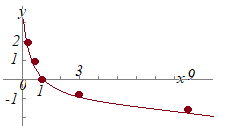
1. 底が1よりも大きな異なる数のとき, 2. 底が1よりも小さな異なる数のとき,
2. 底が1よりも小さな異なる数のとき,