|
対数不等式の解き方
底aが a>1のとき
logax>logat → x>t
(解説)底aが 0<a<1のとき logax>logat → x<t 右図1に示されるように, 底aがa>1のとき,グラフは単調増加関数（右上がりのグラフ）だから, logax>logatならば,x>tが成り立ちます. 底aが0<a<1のとき,グラフは単調減少関数（右下がりのグラフ）だから, logax>logatならば,x<tが成り立ちます.
注意
0<a<1のとき,対数を外したとき不等号の向きが逆になります. |
このページの「マイナーチェンジありカバー版」「パソコン用」ページ
（グーグルブロガー版）は，こちら⇒ 図1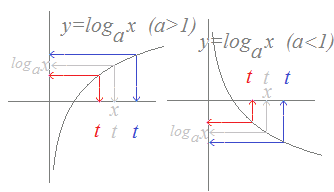 
対数方程式の場合と同様に, 真数は正の数でなければなりません.
例1次の対数不等式を解いてください.この真数条件は元の不等式で確かめる必要があり,元の不等式を変形したものでは一般に条件が変わってしまいます.
log10(2x−1)<log10x
真数条件から2x−1>0, x>0 → x> …(1) 底は1よりも大きいから, 2x−1<x x<1 …(2) (1)(2)→ <x<1 …(答) |
|
例2次の対数不等式を解いてください.
log10x+log10(x−1)<log106
真数条件からx>0 かつ x−1>0 → x>1 …(1) 両辺を係数1の１つのlogにまとめる. log10x(x−1)<log106 底は1よりも大きいから, x(x−1)<6 2次不等式を因数分解で解くと x2−x−6<0 (x−3)(x+2)<0 −2<x<3 …(2) (1)(2)→ 1<x<3 …(答) |
例3次の対数不等式を解いてください.
2 log0.5(x−4)≦log0.52x
真数条件からx−4>0 かつ x>0 → x>4 …(1) 両辺を係数1の１つのlogにまとめる. log0.5(x−4)2≦log0.52x 底は1よりも小さいから, (x−4)2≧2x 2次不等式を因数分解で解くと. x2−8x+16≧2x x2−10x+16≧0 (x−8)(x−2)≧0 x≦2 or 8≦x …(2) (1)(2)→ x≧8 …(答) |
|
例4次の対数不等式を解いてください.
1.log10(3−x)>log10(x−1)
(解答)真数条件から 3−x>0 → x<3 x−1>0 → 1<x ∴ 1<x<3…(1) 底10は1よりも大きいから,対数を外すと不等号の向きは同じになる. 3−x>x−1 −2x>−4 x<2 …(2) (1)(2)→ 1<x<2 …(答) |
2.log0.2(2x−4)>log0.2(x+1)
(解答)真数条件から 2x−4>0 → x>2 x+1>0 → x>−1 ∴ x>2…(1) 底0.2は1よりも小さいから,対数を外すと不等号の向きは逆になる 2x−4<x+1 x<5 …(2) (1)(2)→ 2<x<5 …(答) |
|
3.log2x+log2(x−2)≧3
(解答)真数条件から x>0, x−2>0 → x>2 …(1) 両辺を係数1の１つのlogにまとめる. log2x(x−2)≧3log22=log28 底2は1よりも大きいから,対数を外すと不当後の向きは変わらない. x(x−2)≧8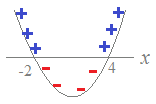 
2次不等式を因数分解で解くとx2−2x−8≧0 (x+2)(x−4)≧0 x≦−2 or 4≦x …(2)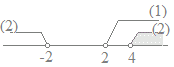 
(1)(2)→4≦x …(答) |
4.log(x+1)<log(x+8)−log(x−4)
(解答)真数条件から x+1>0 → x>−1 x+8>0 → x>−8 x−4>0 → x>4 ∴ x>4…(1) 係数が負となっている項を移項すると log (x+1)+log(x−4)<log(x+8) 両辺を係数1の１つのlogにまとめると log(x+1)(x−4)<log(x+8) 底は1よりも小さいから,対数を外すと不等号の向きが逆になる (x+1)(x−4)>x+8  2次不等式を因数分解で解くとx2−3x−4>x+8 x2−4x−12>0 x<−2 or 6<x …(2)  (1)(2)→x>6 …(答) |
|
問題次の対数不等式を解いてください. (空欄を埋める) |