|
����̕ϊ�����
a,b>0, a≠1�̂Ƃ��C�C�ӂ̒�c>0, c≠1�ɑ���
�i�ؖ��jlogab= �����藧�D
�i���K�j
logab=x …(A)(b>0, a>0, a≠1)�Ƃ������ΐ��̒�` logay=x ←→ y=ax (y>0, a>0, a≠1) �^���̗ݏ�̑O�ɕt���W�� logaMn=n logaM …(*) 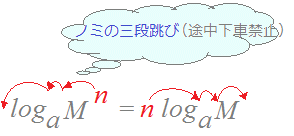
b=ax …(B) (B)�̗��ӂɒ��c�Ƃ���ΐ����Ƃ�� (c>0, c≠1) logcb=logcax logcb=x logca ←�^���̗ݏ� logcb=logab · logca ← (A) ���������� logab= |
�i���͋��F�}���ɂ��Ăق����Ƃ����l�ւ̉���j ���ΐ�logab�́Cy=�ō����}�̂悤�Ȑ}�`�̖ʐϔ��\���D 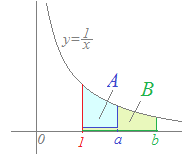 �@�Ȃ����Ƃ������Ƃ́C���w�V�ŏK���̂ŁC�����ł͂Ƃ肠�����u�ΐ��Ƃ͖ʐς̔�v�Ƃ������Ƃ������������Ă����Ƃ悢�D
�@�Ȃ����Ƃ������Ƃ́C���w�V�ŏK���̂ŁC�����ł͂Ƃ肠�����u�ΐ��Ƃ͖ʐς̔�v�Ƃ������Ƃ������������Ă����Ƃ悢�Dlogab= �@�܂�Clogab�Ƃ́C�}��A�� �ʐς���i����j�Ƃ����Ƃ��́CB�̖ʐς�\���D
���M�҂����P�̂Ƃ��Ɂu�ȁ[�D�ΐ��Ȃ�āC�����̕��������v�ƌ�������C�����̐搶�ɃJ���J���ɓ{��ꂽ�D�搶�Ƃ��ẮCb/a �ł͂Ȃ��C�ʐς̔䂾�ƌ������������悤���D���͂������������肾�����
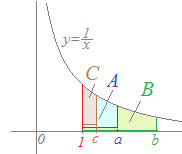 �@����ɑ��āC�}��C�̖ʐς���Ƃ��ĕ\���ƁC
�@����ɑ��āC�}��C�̖ʐς���Ƃ��ĕ\���ƁClogca= logcb= �@ ������ �@ �����藧�D �� (1)log23=== (2)log84==
”�ΐ����Ƃ�”�Ƃ́C”�ΐ�����菜������”�ł͂Ȃ� logab → b ←�~
”�ΐ����l���邱��”��\���D
b → logcb�i���c�j ←�� ax → logcax�i���c�j ←�� ���̌v�Z�����͒ꂪ�������ꍇ�Ɍ��萬�藧�D
1.logaM+logaN=logaMN
�قȂ��ŕ\���ꂽ�ΐ��ɂ��āC��L�̂悤�Ȍv�Z���s���ɂ́C���炩���ߒꂪ�������ΐ��ɏ��������Ă����Ȃ���Ȃ�Ȃ��D
2.logaM−logaN=loga 3.n logaM=loga(M n)=logaM n |
|
�����̑ΐ����ȒP�ɂ���D
(1)log23·log32
�i�jlog23·log32=log23 =log22=1 �i�ʉ��j log23·log32= =1
(2)log56·log67·log75
�i�jlog56·log67·log75= =1 |
(3)log84
�i�jlog84====
(4)log9
�i�jlog9====−2 |
|
���P���̑ΐ����ȒP�ɂ���D �i�߂�j |
|
�ΐ������Ǝw���������������Ƃ��C���̊W�����藧�D
�w������^���Ƃ���ΐ��́C�������g�ɓ������D
logaax=x …(I) �w�����̗ݏ悪�ΐ��ƂȂ��Ă�����̂́C�������g�ɓ������D alogax=x …(II) |
�i�ؖ��j I ← logaax=x logaa=x ←(*) II ← logax=logax ←���炩 �ΐ��̒�`�ɂ�� y=logax → ay=x logax=logax → alogax=x |
|
���Q���̑ΐ����ȒP�ɂ���D �i�߂�j |