maximaの初歩的な操作14･･･重積分

== maximaの初歩的な操作 ==
･･･重積分･･･
○Xmaxima，wxMaxima のインストール方法，基本操作については［この頁］参照

○Xmaximaでは，数式がアスキーアート風に出力されることが多い．wxMaximaでは数学で通常用いる記号に近い形で結果が示される．以下ではwxMaiximaを用いた場合の例と答を示す．

○wxMaximaでの入力
メニューから［微積分］→［積分］を選ぶと，対話型記入欄になるので
関数，変数を入力し，定積分にチェックを付ける．積分区間の下端，上端にπや∞などの記号定数を使うときは選択肢から選ぶこともできる．

○入力に当たっては，2xなどの書き慣れた記号を2*xと書かなければならないことに注意しましょう．べき乗（指数）を2^nなどと書くのは，TeXの書き方とほぼ同じ

〇 wxMaximaのメニュー画面から重積分を直接選択することはできないので，「微積分」→「積分」と進んで，

関数%
変数x
レ定積分 ←チェックを入れる
上端0
下端1

の形にして「OK」ボタンを押すと，入力欄に次の式が書き込まれる．

integrate(%, x, 0, 1);

これは（一重）積分の計算を表しているので，この式の % 欄にキーボードからネスト（入れ子）になるように次のように書き足すと，重積分の計算ができます．

integrate(integrate(%, y, 0, 1);, x, 0, 1);

この式は，次の計算に対応しています．

$\int_0^1\{\int_0^1...dy\}dx$

そこで,被積分関数を%欄に，積分区間の下端，上端を書き込んでShift+Enterとすれば，重積分の結果が得られます．

(1) $\int_0^1\{\int_0^2(x+ y)dy\}dx$ を求めるには．
(2) $\int_0^2\{\int_0^1(x+ y)dx\}dy$ を求めるには．

(1)
wxMaximaでの入力
integrate(integrate(x+y,y,0,2), x, 0, 1);
結果
$3$
(2)
wxMaximaでの入力
integrate(integrate(x+y,x,0,1), y, 0, 2);
結果
$3$

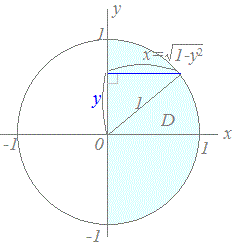(3) $D\hspace{2}:\hspace{2}x^2+ y^2\underline{\le}1,\hspace{3}x\underline{\ge}0$ のとき
$\int\int_D 2xy^2dxdy$ を求めるには．

右図のように，
各々の $y$ に対して， $0\underline{\le}x\underline{\le}\sqrt{1-y^2}$ となる $x$ の範囲で横方向に積分してから，
求めた被積分関数を $y$ について積分すればよいから
wxMaximaでの入力
integrate(integrate(2*x*y^2,x,0,sqrt(1-y^2)), y, -1, 1);
結果
$\frac{4}{15}$

（別の方法）
右図のように，
各々の $x$ に対して， $-\sqrt{1-x^2}\underline{\le}y\underline{\le}\sqrt{1-x^2}$ となる $y$ の範囲で縦方向に積分してから，
求めた被積分関数を $x$ について積分すればよいから
wxMaximaでの入力
integrate(integrate(2*x*y^2,y,-sqrt(1-x^2),sqrt(1-x^2)), x, 0, 1);
結果
$\frac{4}{15}$

(4) $\int_0^1\{\int_{x^^2}^x 2xydy\}dx$ を求めるには．

右図（青線）のように，
各々の $x$ に対して， $x^2\underline{\le}y\underline{\le}x$ となる $y$ の範囲で縦方向に積分してから，
求めた被積分関数を $x$ について0から1まで積分すればよい
wxMaximaでの入力
integrate(integrate(2*x*y,y,x^2,x), x, 0, 1);
結果
$\frac{1}{12}$

（積分順序を変更する場合）
右図（赤線）のように，
各々の $y$ に対して， $y\underline{\le}x\underline{\le}\sqrt{y}$ となる $x$ の範囲で横方向に積分してから，
求めた被積分関数を $y$ について0から１まで積分すればよいから
wxMaximaでの入力
integrate(integrate(2*x*y,x,y,sqrt(y)), y, 0, 1);
結果
$\frac{1}{12}$

...（PC版）メニューに戻る