maximaの初歩的な操作16･･･テイラー級数

== maximaの初歩的な操作16･･･テイラー級数 == ○Xmaxima，wxMaxima のインストール方法，基本操作については［この頁］参照

○wxMaximaでテイラー級数を求めるには
メニューから［微積分］→［テイラー級数］を選ぶと，対話型記入欄になるので
関数，変数，値の入力，次数の指定を埋めて，ＯＫボタンを押します．

　「値の入力」の部分の数字がaであればx−aのべきで展開されます．初期設定のまま「値の入力」の部分の数字を0とした場合は，マクローリン級数と呼ばれるものになりますが，この場合もテイラー級数に含めて考えます．
　「次数の指定」によって第何項まで（xnまで）表示するかが決まります（係数が０の項があれば，見かけ上はこれよりも少なくなります）

○関数の入力に当たっては，2xなどの書き慣れた記号を2*xと書かなければならないことに注意しましょう．べき乗（指数）を2^nなどと書くのは，TeXの書き方とほぼ同じ

【wxMaximaでテイラー級数を求めるには】

○原点0の周りでのテイラー級数（=マクローリン級数）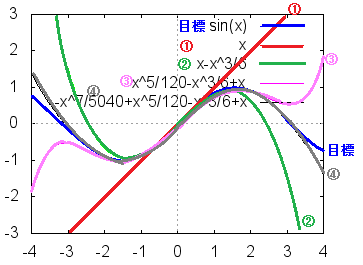

○マクローリン展開は，原点0付近での関数の様子をxの多項式として近似して示すものです．理論上，無限級数まで考えれば目標とする関数に収束しますが，実用上は必要な精度までの項数を使って

f(x)=a0+a1x+a2x2+a3x3+a4x4+ ...
の形で考えます．

この係数akが（高次の）微分係数を用いて
$\frac{f^{(k)}(0)}{k!}$
と表せるので，マクローリン展開は次の形に書けることになります．
$f(x)=f(0)+ \frac{f^{'}(0)}{1!}x+ \frac{f^{('')}(0)}{2!}x^2+ \frac{f^{(3)}(0)}{3!}x^3+ ...$

○右のグラフは下記の例のうちでy=sinxの関数について，マクローリン展開の第何項まで使ったかに応じて近似の精度がよくなっていく様子を表したものです．（sinxのように係数が正負交互に現れる場合は，近似曲線は行ったり来たりしながら近づきます．）

○例えば，x=0.1の値で考えて見ると，xの項が小数第１位，x2の項が小数第２位，x3の項が小数第３位，…というように順次精度の高い桁数まで求められるということになります．

○このようにテイラー級数（テイラー展開）は，局所的に各々の点のまわりでの関数の様子を調べるのに使われます．

※上のグラフからも分かるように，x=0から離れた点では目標とする関数の近似が悪くなり，テイラー展開（マクローリン展開）の項数をもっと増やさないと十分な近似にはなりません．（項数（次数）を限りなく増やしていけば，いくらでも正確に近似できます．）
　これに対して別の項目で述べるフーリエ級数は，個別の点については精度はそこそこながら大域的な近似を能率よく与えることができます．
　テイラー級数を使うか，フーリエ級数を使うかは調べたい内容によって使い分けます．

関数	入力メニューをたどれば次のコマンドが自動的に入ります
$e^x$	taylor(%e^x, x, 0, 8);
≪結果≫ $1+ x+ \frac{x^2}{2}+ \frac{x^3}{6}+ \frac{x^4}{24}+ \frac{x^5}{120}+ \frac{x^6}{720}+ \frac{x^7}{5040}+ \frac{x^8}{40320}+ ...$ …(1) 公式集では，次の形で書かれる $1+ x+ \frac{x^2}{2!}+ \frac{x^3}{3!}+ \frac{x^4}{4!}+ \frac{x^5}{5!}+ \frac{x^6}{6!}+ \frac{x^7}{7!}+ \frac{x^8}{8!}+ ...$ または $\sum_{k=0}^{\infty} \frac{1}{k!}x^k$ 筆算で求めるには $f(x)=e^x\rightarrow f^{(k)}(x)=e^x$ だから $f(0)=1$ ， $f^{(k)}(0)=1$ ， $\frac{f^{(k)}(0)}{k!}=\frac{1}{k!}$ $f(x)=f(0)+ \frac{f^{'}(0)}{1!}x+ \frac{f^{('')}(0)}{2!}x^2+ \frac{f^{(3)}(0)}{3!}x^3+ ...$ $=1+ x+ \frac{x^2}{2!}+ \frac{x^3}{3!}+ ...$
$\sin x$	taylor(sin(x), x, 0, 8);
≪結果≫ $x- \frac{x^3}{6}+ \frac{x^5}{120}- \frac{x^7}{5040}+ ...$ …(2) 公式集では，次の形で書かれる $x- \frac{x^3}{3!}+ \frac{x^5}{5!}- \frac{x^7}{7!}+ ...$ または $\sum_{k=0}^{\infty} (-1)^k\frac{x^{2k+ 1}}{(2k+ 1)!}$ 筆算で求めるには $f(x)=\sin x \rightarrow f^{'}(x)=\cos x \rightarrow f^{''}(x)=-\sin x \rightarrow f^{(3)}(x)=-\cos x$ $\rightarrow f^{(4)}(x)=\sin x$ だから $f(0)=0,f'(0)=1,f''(0)=0,f~{(3)}(0)=-1,f^{(4)}(0)=0$ $f(x)=f(0)+ \frac{f^{'}(0)}{1!}x+ \frac{f^{('')}(0)}{2!}x^2+ \frac{f^{(3)}(0)}{3!}x^3+ ...$ $0+ x + 0- \frac{x^3}{6}+ 0 ...$
$\cos x$	taylor(cos(x), x, 0, 8);
≪結果≫ $1- \frac{x^2}{2}+ \frac{x^4}{24}- \frac{x^6}{720}+ \frac{x^8}{40320}- ...$ …(3) 公式集では，次の形で書かれる $1- \frac{x^2}{2!}+ \frac{x^4}{4!}- \frac{x^6}{6!}+ ...$ または $\sum_{k=0}^{\infty} (-1)^k\frac{x^{2k}}{(2k)!}$
$\tan x$	taylor(tan(x), x, 0, 8);
≪結果≫ $x+ \frac{x^3}{3}+ \frac{2x^5}{15}+ \frac{17x^7}{315}+ ...$ …(4)
$\log(1+ x)$	taylor(log(1+x), x, 0, 6);
≪結果≫ $1- \frac{x^2}{2}+ \frac{x^3}{3}- \frac{x^4}{4}+ \frac{x^5}{5}- \frac{x^6}{6}+ ...$ …(5)

○原点以外の点の周りでのテイラー級数

○テイラ－展開は，点a付近での関数の様子をx−aの多項式として近似して示すものです．

f(x)=a0+a1(x−a)+a2(x−a)2+a3(x−a)3+a4(x−a)4+ ...
の形で考えます．

この係数akが（高次の）微分係数を用いて
$\frac{f^{(k)}(a)}{k!}$
と表せるので，テイラー展開は次の形に書けることになります．
$f(x)=f(a)+ \frac{f^{'}(a)}{1!}(x-a)+ \frac{f^{('')}(a)}{2!}(x-a)^2+ \frac{f^{(3)}(a)}{3!}(x-a)^3+ ...$

関数 $\sin x$ （ $x=\frac{\pi}{2}$ の周りでの展開式）	taylor(sin(x), x, %pi/2, 6);
≪結果≫ $1- \frac{(x-\frac{\pi}{2})^2}{2}+ \frac{(x-\frac{\pi}{2})^4}{24}- \frac{(x-\frac{\pi}{2})^6}{720}+ ...$ 筆算で求めるには，テイラーの定理に直接代入するとよい $f(x)=\sin x \rightarrow f^{'}(x)=\cos x \rightarrow f^{''}(x)=-\sin x \rightarrow f^{(3)}(x)=-\cos x$ $\rightarrow f^{(4)}(x)=\sin x$ だから $f(\frac{\pi}{2})=1,f'(\frac{\pi}{2})=0,f''(\frac{\pi}{2})=-1,f~{(3)}(\frac{\pi}{2})=0,f^{(4)}(\frac{\pi}{2})=1$ $f(x)=f(\frac{\pi}{2})+ \frac{f^{'}(\frac{\pi}{2})}{1!}(x-\frac{\pi}{2})+ \frac{f^{('')}(\frac{\pi}{2})}{2!}(x-\frac{\pi}{2})^2+ \frac{f^{(3)}(\frac{\pi}{2})}{3!}(x-\frac{\pi}{2})^3+ ...$ $=1+ 0- \frac{(x-\frac{\pi}{2})^2}{2}+ 0 + \frac{(x-\frac{\pi}{2})^4}{24} + 0- \frac{(x-\frac{\pi}{2})^6}{720}+ ...$ 次のように考えてもよい $x=\frac{\pi}{2}$ の周りの展開式を求めるということは $x-\frac{\pi}{2}$ の多項式で表すということだから $\sin x=\sin((x-\frac{\pi}{2})+ \frac{\pi}{2})$ ここで三角関数の公式 $\sin(\alpha + \frac{\pi}{2})=\cos x$ を使うと $\sin((x-\frac{\pi}{2})+ \frac{\pi}{2})=\cos(x-\frac{\pi}{2})$ 上記の(3)の結果から $\cos x=1- \frac{x^2}{2}+ \frac{x^4}{24}- \frac{x^6}{720}+ \frac{x^8}{40320}- ...$ だから $\sin x=\cos(x-\frac{\pi}{2})=1- \frac{(x-\frac{\pi}{2})^2}{2}+ \frac{(x-\frac{\pi}{2})^4}{24}- \frac{(x-\frac{\pi}{2})^6}{720}+ ...$
関数 $\frac{1}{x}$ （ $x=1$ の周りでの展開式）	taylor(1/x, x, 1, 6);
≪結果≫ $1-(x-1)+(x-1)^2-(x-1)^3+(x-1)^4-(x-1)^5+(x-1)^6 ...$ 筆算で求めるには，テイラーの定理に直接代入するとよい $f(x)=\frac{1}{x}=x^{-1} \rightarrow f^{'}(x)=-x^{-2} \rightarrow f^{''}(x)=2x^{-3}$ $\rightarrow f^{(3)}(x)=-6x^{-4}$ だから $f(1)=1,f'(1)=-1,f''(1)=2,f~{(3)}(1)=-6$ $f(x)=f(1)+ \frac{f^{'}(1)}{1!}(x-1)+ \frac{f^{('')}(1)}{2!}(x-1)^2+ \frac{f^{(3)}(1)}{3!}(x-1)^3+ ...$ $=1-(x-1)+(x-1)^2-(x-1)^3+(x-1)^4-(x-1)^5+(x-1)^6 ...$
関数 $A_0+ A_1(x-a) + A_2(x-a)^2$ （ $x=b$ の周りでの展開式）	taylor(A_0+A_1(x-a)+A_2(x-a)^2, x, b, 3);
≪結果≫ $A_0+ (-a+ b)A_1+ (a^2-2ba+ b^2)A_2+ ((-2a+ 2b)A_2+ A_1)(x-b)+ A_2(x-b)^2$ この問題はテイラー展開を使わなくても，高校で習う恒等式の係数比較でも解ける．また，見かけ上は...で示されているが3次式以上はない．一般にある点 $a$ の周りの展開式は任意の点 $b$ の周りの展開式に直すことができ， $A_0+ A_1(x-a) + A_2(x-a)^2=f(x)$ とおくと $f(x)=f(b)+ f'(b)(x-b) + \frac{f''(b)}{2!}(x-b)^2$ において $f(b)=A_0+ A_1(b-a)+ A_2(b-a)^2$ $f'(b)=A_1+ 2A_2(b-a)$ $\frac{f''(b)}{2!}=A_2$ となる．（第４項以降は０）例えば， $3+ 4(x-1) + 5(x-1)^2=B_0 + B_1(x-2)+ B_2(x-2)^2$ となる係数 $B_0 , B_1 ,B_2$ はtaylor(3+4(x-1)+5(x-1)^2, x, 2, 3);により直ちに求めることができ， $B_0=12 , B_1=14 ,B_2=5$ となる．

...メニューに戻る　

..maximaのメニューに戻る