← PC用は別頁
|
※中学3年生向け「平行線と相似」について,このサイトには次の教材があります. この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は,他の頁を見てください. が現在地です. |
|
※中学3年生向け「平行線と相似」について,このサイトには次の教材があります. この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は,他の頁を見てください. が現在地です. |
|
○1 2つの三角形の高さが等しいときは,面積の比は底辺の長さの比に等しい.
△ABC = △ABD = ここで BC:BD=a:b ならば △ABC:△ABD = となって,△ABC と△ABD との面積比は底辺の長さの比に等しくなる. 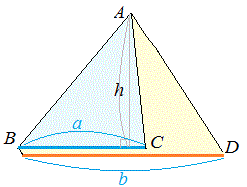 -- 図1 --
【例1】
図2において△ABC と△ABD の高さは等しいから, △ABC:△ABD=2:3 △ABC:△ACD=2:1 |
|
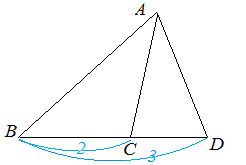 -- 図2 -- |
|
|
○2 2つの三角形の底辺の長さが等しいときは,面積の比は高さの比に等しい.
○2の証明○3 高さが書いていないときでも,1組の辺の比がm:n のときは,高さがm:n と考えてよい. 三角形の面積は(底辺)×(高さ)÷2で求められる.図3の△FBC と△ABC の面積は各々 △FBC = △ABC = ここで底辺 BC は共通だから △FBC : △ABC= 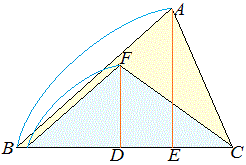 -- 図3 -- 図3の△FBD と△ABE は相似図形だから, FD:AE=FB:AB したがって △FBC : △ABC= FD : AE = FB : AB
【例2】
図4において△DBC と△ABC の底辺BC は共通だから, △DBC:△ABC=3:5 △DBC:△ADC=3:2 |
|
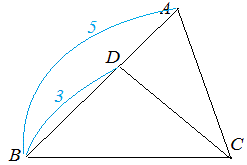 -- 図4 -- |
|
|
○4
2つの三角形の底辺の比がa:b ,高さの比がm:n のとき,面積の比はam:bn になる. ○5 図6のように2つの三角形で1つの角が共通のとき,この角をはさむ2辺の比が各々a:b ,m:n のとき,面積の比はam:bn になる. 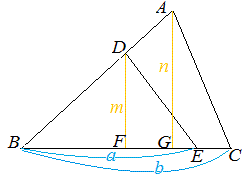 -- 図5 -- △DBE = △ABC = だから △DBE : △ABC = ○5の証明 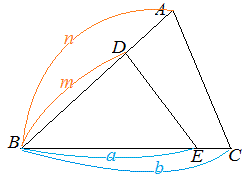 -- 図6 -- △DBE : △ABC = am : bn
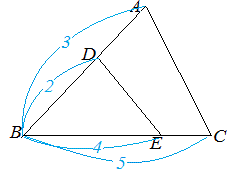
【例3】
図7において
△DBE:△ABC=8:15
△DBE:(四角形)ADEC=8:(15-8)=8:7 |
|
 -- 図7 -- |
|
|
○6 相似比がa:b となる2つの三角形の面積の比はa2:b2 になる.
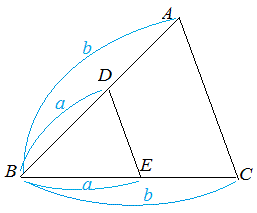 -- 図8 -- ○5において底辺の比も高さの比もa:b になるから, △DBE : △ABC = aa : bb = a2:b2 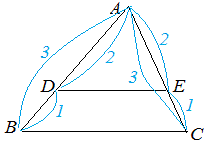 【例4】 【例4】右図において △ADE:△ABC=4:9 △ADE:(四角形)DBCE=4:(9-4)=4:5 |
|
|
【まとめ】
(1) 図9ののように2つの三角形の底辺の比がa:b,高さの比がm:n のとき,面積の比はam:bn になる.(右の図9では高さの比をm:n と読む.)  -- 図9 -- △BEP:△CAP=8:15 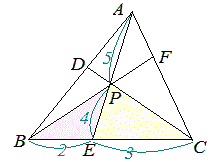 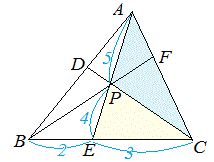 -- 図10 -- |
|
【例題1】
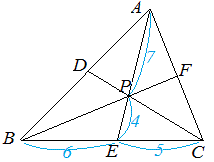 -- 図11 -- (1) △BEP:△CEP=6:5
高さが等しく,底辺が6:5と見る
(2) △ABC:△PBC=11:4
底辺が等しく,高さが11:4と見る
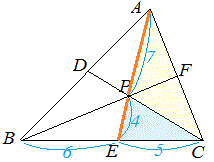 (3) △APC:△PEC=7:4 (3) △APC:△PEC=7:4
右図のようにAP , PE を底辺とみると,高さが等しく,底辺が7:4
(4) △APB:△BPC=21:22△APB:△BPC=21:22 |
|
【例題2】 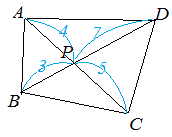 -- 図12 -- (1) △APB:△BPC=4:5
高さが等しく,底辺が4:5と見る
(2) △BPC:△CPD=3:7
高さが等しく,底辺が3:7と見る
(3) △APB:△CPD=12:35△APB:△CPD=12:35 |
|
【例題3】 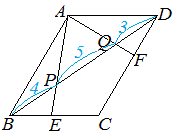 -- 図13 -- (1) △ABQ∽△FDQ (相似比は9:3=3:1)だから
△ABQ:△FDQ=32:12=9:1
(2) △BEP∽△ADP (相似比は4:8=1:2)だから△ABP:△ABQ=4:9 (高さが等しく底辺が4:9) ゆえに △ABP:△FDQ=4:1
△BEP :△ADP=1:4
△APQ :△APD=5:8 (高さが等しく底辺が5:8)
ゆえに
△BEP:△APQ = |
|
【例題4】
(5)の証明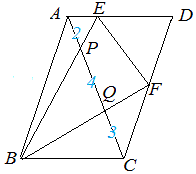 -- 図14 -- (1)
△APE∽△CPB (相似比は AP:PC=2:7)
EP:PB=2:7 △APE と△APB は高さが等しく底辺が 2:7
△APE:△APB=2:7
(2)
△APE:△QPB=1:7
(3)
△BQA∽△FQC
だから BQ:QF=AQ:QC=6:3=2:1 △CQB と△FQC は高さが等しく底辺が 2:1
△CQB:△FQC=2:1
(4)
△CQF:△FED=7:15
(5)
△BQP:△DEF=56:45
AP:PC=2:7だからAE:BC=2:7
したがってAE:ED=2:5 AQ:QC=6:3だからAB:CF=6:3 したがってCD:CF=6:3,CF:FD=3:3=1:1
△ABC=△CAD ←平行四辺形だから
ゆえに
|
|
(2)の別解
△APE:△QPB=1:7
(4)の証明
△APE∽△CPB だから AE:CB=AP:CP=2:7 AE:DA=2:7 (←平行四辺形だから) AE:ED=2:5 ----------------------- △AQB∽△CQF だから AB:CF=AQ:QC=6:3=2:1 DC:CF=2:1 (←平行四辺形だから) CF:FD=1:1 -----------------------
△CQF:△FED=7:15
|
|
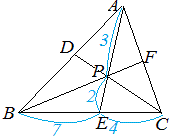
【問題1】
 |
|
(1) △BEP と△CEP は高さが等しく,底辺が7:4 だから △BEP: △CEP=7:4 (2) △ABC と△PBC は底辺が等しく,高さが5:2 だから △ABC: △PBC=5:2 (3) △APC と△PEC の底辺を各々AP , PE と見ると,高さが等しく,底辺が3:2 だから △APC: △PEC=3:2 (4) △BCP:△CAP=11:6 |
|
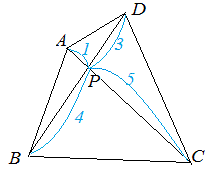
【問題2】
 |
|
(1) △APB:△APD=4:3
(2) △APD:△CPD=1:5 |
|
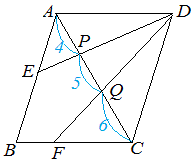
【問題3】
 |
|
(1) △EPA∽△DPC で相似比が 4:11 だから面積比は
△DPC:△DPQ=11:5 ゆえに だから △CQF:△PQD=4:5 |
|
|
| ■このサイト内のGoogle検索■ |