■１次変換の定義
○座標平面から座標平面への写像で，点(x, y)の像(x', y')が，次のような定数項のない１次式で表されるものを１次変換といいます．
.

○　行列で書かれた等式は，対応する各成分が等しいことを表します．
　例えば，２×１行列の等式=は
連立方程式と同値です．
　また，行列の積は２×１行列に等しい
ので，次の行列の等式は上記の連立方程式(1)(2)と同値になります．
.=
○　このように１次変換は係数行列によって定まるので， １次変換
.すなわち=
を，行列が表す１次変換といいます．
○　集合Aの各々の要素xに集合Bの要素yを対応させる規則が与えられているとき，この対応y=f(x)をAからBへの写像（または関数）といいます．
　一般の写像においては，集合Aを集合Bとは異なる集合である場合もあります．
【例】　ベクトルの内積
(a, b)·(c, d)→ ac+bd
は平面上の２つの点から１つの実数への対応になっています．


○　写像のうちで，特に同一集合から同一集合への対応となってるものを変換といいます．
　座標平面から座標平面への対応を与えている写像は，変換です．
■合成変換の定義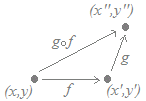
○１次変換f:=
によって，点(x, y)が点(x', y')に移され，
　１次変換g:=
によって，点(x', y')が点(x'', y'')に移されるとき，点(x, y)に点(x'', y'')を対応させる変換をこれら２つの変換の合成変換といいます．

【重要】
１次変換f, gを表す行列が各々A, Bであるとき，
合成変換g○fを表す行列は，行列の積BAになります．
合成変換を表す記号g○fについても，行列の積についても，「後から行う操作」に対応する方が「左側」に着きます．
（解説）
f:=…(1)においてA=
g:=…(2)においてB=
とおくとき，(1)を(2)に代入すると
==
だから
=BA
【例１】
　１次変換f, gを表す行列が各々,
であるとき，合成変換g○f, f○g, f○fを表す行列を求めてください．
（解答）
g○fを表す行列は=
f○gを表す行列は=
f○fを表す行列は=
【問題１】
　１次変換f, gを表す行列が各々,
であるとき，合成変換g○f, f○g, f○fを表す行列を求めてください．（下の選択肢から選んでください）
g○fを表す行列
. . . .
f○gを表す行列
. . . .
f○fを表す行列
. . . .
【問題２】
　,
のとき，x'', y''をx, yで表す式を求めてください．
. .
. .
【問題３】
　a≠0またはb≠0のとき，行列で表される１次変換
は，原点の周りの角θの回転を表す１次変換f
.f:=
と原点を中心とする相似拡大（または縮小）を表す１次変換g
.f:=r=
の合成変換で表すことができます．
　次の行列で表される１次変換を回転と拡大の合成と見なしたとき，回転角0≦θ<2πと拡大比r>0は各々幾らになりますか．
. θ= , r=1 . θ= , r=2
. θ= , r= . θ= , r=
【合成変換を表す記号】
　点の座標(x, y), (x', y')はその位置ベクトル, , で表すことができるので，
.=(x, y)
.=(x', y')
.=(x'', y'')
とおくと
各々の１次変換が
.=f()…(1)
.=g()…(2)
で表されるとき，(1)を(2)に代入すると
.=g(f())
となりますが，このg(f())を
記号g○f() またはg○fで表します．
＃＃危険な落とし穴＃＃
　g○fはg(f())のことなので，先に１次変換fによって移し，次に１次変換gによって移された結果を表します．
　見かけ通りに前から順に読んでしまって，gが先だと考える間違いが多いので注意しましょう．
（参考）
Excelを使って行列の積を検算する方法
　 ABCDEFGH
110
23
23
22-1
1-1
37
　上の表のようにセルA1〜B2に行列Pの成分が書きこまれていて，セルD1〜E2に行列Qの成分が書きこまれているときに，これらの行列の積PQをセルG1〜H2に書き込むには，
○　行列の積を求めるワークシート関数は =MMULT()です．そこで，G1をポイントしておいて
=MMULT(A1:B2, D1:E2)
と書き込みます．
○　≪ここからが重要≫
　以上の操作では，G1に１行１列成分が書き込まれるだけで，他の行列成分は書き込まれません．（数式のコピペなどをしてもだめです）
　行列として一体の「配列」に直すには，次のようにします．
(1)　G1〜H2までを選択して反転表示にしておきます．
(2)　Excel画面の上の方にある数式バーにマウスを当てて，Ctrl+Shift+Enter（CtrlキーとShiftキーを押しながら，Enterキーを押す）

○　行列の掛け算の順序を入れ替えたり，同じ行列の積を求める場合でも，
=MMULT(D1:E2, A1:B2)
=MMULT(A1:B2, A1:B2)
のように，引数を入れ替えるだけでできます．

.
.
.
【逆変換】
○　１次変換fを表す行列がAであるとき，Aの逆行列A−1が存在すれば
.f:=A…(1)
の逆変換f−1は，逆行列A−1で表され
.f−1:=A−1 …(2)
となります．

○　１次変換f, gを表す行列が各々A, Bで，A, Bの逆行列A−1, B−1が存在するとき，
　合成変換f○gの逆変換
.(f○g)−1=g−1○f−1は(AB)−1=B−1A−1…(3)
で表されます．
　合成変換g○fの逆変換
.(g○f)−1=f−1○g−1は(BA)−1=A−1B−1…(4)
で表されます．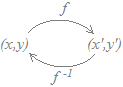

○　１次変換fを表す行列がAで，Aの逆行列A−1が存在するとき，逆変換の逆変換は元の変換と等しくなり，その行列はAになります．
.(f−1)−1=f ⇔ (A−1)−1=A…(5)
○　また，逆変換（逆行列）が存在するとき，１次変換fとその逆変換f−1との合成変換は恒等変換I（行列で書けばE）になります．
.f−1○f=I , f○f−1=I ⇔ A−1A=E , AA−1=E…(6)
（解説）
(1)(2)←
A−1が存在すれば
.=A
の両辺に「左から」A−1を掛けると
.A−1 =A−1A=E=
したがって，逆向きの対応は
.=A−1
で表されます．
(3)←
A−1, B−1が存在すれば
.=AB
の両辺に「左から」B−1A−1を掛けると
.B−1A−1=B−1A−1AB=
.=B−1A−1
となるから，(AB)−1=B−1A−1
(4)も同様
【例２】
　次の１次変換について，逆変換の式を求めてください．
.=
　
（解答）
　行列について，D=2×3−1×5=1だから
　逆行列は−1=
　したがって，逆変換の式は
.=
（復習）【逆行列の求め方】
　行列A=について，その行列式D=ad−bcが0で
なければ，行列Aの逆行列A−1が存在し
　A−1=
が成り立ちます．

（参考）
【逆行列が存在する場合と存在しない場合の対応の違い】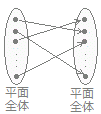
○　行列A=の行列式
D=ad−bcが0でないとき，
行列Aは正則であるといい，座標平面上の点(x, y)から(x', y')への対応は１対１になります．
(1) (x, y)が座標平面上のすべての点をとるとき，(x', y')もすべての点をとります．（全射）
(2) 異なる(x, y)には，異なる(x', y')が対応します．（単射）
したがって，平面上の任意の(x', y')に対して（全射だから）,元の(x, y)がただ一つ（単射だから）存在します．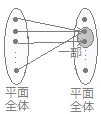

○　行列A=の行列式
D=ad−bcが0であるとき，
行列Aは正則でないと言われ，座標平面上の点(x, y)から(x', y')への対応は１対１になりません．
(1) (x, y)が座標平面上のすべての点をとっても，(x', y')はすべての点をとりません．平面上の一部分になります（全射でない）
(2) 異なる(x, y)には，同一の(x', y')が対応する場合があります．（単射でない）
したがって，平面上のある(x', y')に対して，元の(x, y)が存在しないことがあります．（元が全射でないから）
　平面上のある(x', y')に対して，元の(x, y)が複数個存在することがあります．（元が単射でないから）

○　以上のように，１次変換Aによる像(x', y')から原像(x, y)への対応が座標平面上のすべての点(x', y')に対して定義できるのは逆行列が存在する場合に限ります．
【例３】
　１次変換f, gを表す行列が各々
.A=, B=
であるとき，(f○g)−1を表す行列を求めてください．
（解答）
　f○gを表す行列はABで，その逆変換(f○g)−1を表す行列は(AB)−1=B−1A−1になります．
　実際に求めるには，ABを計算してからその逆行列を求めても，B−1 , A−1をそれぞれ求めてからその積を求めても同じになります．
AB==
その行列式はD=11×(−7)−19×(−4)=−77+76=−1だから
(AB)−1==
【問題４】
　次の１次変換の逆変換を表す式を求めてください．
.=

= . =
= . =
【問題５】
　１次変換f, gを表す行列が各々
.A=, B=
であるとき，(f−1○g)−1を表す行列を求めてください．

.
.
○===高卒〜大学数学基礎メニューに戻る　 ...メニューに戻る