|
��ڎ���
|
|
�@1���ϊ��ɂ���Ď������g�Ɉڂ����_�i�����Ȃ��_�j���s���_�Ƃ����D
(1)�@�ǂ��1���ϊ��ł����_�i��x�N�g���j�͕s���_�ɂȂ��Ă���D�i���_�͕s���_�ł���D�j
�i�ؖ��j
�C�ӂ� �����藧����ł���D
(2)�@�s��
�ƂȂ邱�Ƃł���D
�i�ؖ��j
���_�i��x�N�g���j�ȊO�̕s���_�����݂���Ƃ� �ƂȂ� ���Ȃ킿
�����ŁC(2)�ł́C���̏ؖ����s���悢���ƂɂȂ�D
�@�����C\( \displaystyle (A-E)\vec{x}=\vec{0}\hspace{5px}(\vec{x}\ne \vec{0})\Longleftrightarrow \mid A-E\mid= 0\) �͕K�v�����D �@�\�����������������ƁC���Ȃ킿 \(\Updownarrow\)
\((a-1)\hspace{5px}:\hspace{5px}b=c\hspace{5px}:\hspace{5px}(d-1)\) ←���\(\Updownarrow\)
\(\Bigg\{\begin{array}\{(a-1)&\overset{\times t}{\Longrightarrow}&b\\ c& \overset{\times t}{\Longrightarrow}&(d-1)\end{array}\)�i���̎����W�����ƌ���ƁC���ۂɎ��̂悤�Ɍ��_�i��x�N�g���j�łȂ��������݂��邱�Ƃ�������j �A�j �@���̂Ƃ� �͐��藧�D �@�����C �C�j �@���̂Ƃ� �͐��藧�D �@�����A�j�C�j�Ƃ� �ƂȂ邩��C���ʏ�̂��ׂĂ̓_ |
�y���2.3�z
�i�j�@���̍s��̕\��1���ϊ��ɂ���āC�������g�Ɉڂ����_�i�s���_�j�����߂Ă��������D (1) (2) (1) ������ ������ ������C���ӂ̌W���s��ɂ͋t�s���݂��� �@���_�i��x�N�g���j�݂̂����ƂȂ�…�i���j (2) ������ ��� \(2x+2y=0\) ↓ \(x+y=0\) ↓ ���Ȃ킿�C |
|
�i�ʉ�2�j
�y�t�ϊ������݂��Ȃ��ꍇ�ł��g������@�z
�����̕������F�}��ϐ��\���ɂ��āC�����̕�������x,y���W�ɕ�����D ��}��ϐ��\���ŕ\���� �P���ϊ� �ɂ�� �}��ϐ� �ϐ��� |
�i�ʉ�3�j �����̕������F �́C���̌`�ɏ����� ������s��ŏ����� �ϊ����ɂ͋t�ϊ������݂��邩�炱��𗘗p�ł���D (2)��(1)�ɑ������Cx’, y’�̊W���������� �ϐ��� |
|
�y���10.2�z
�i��1�j---���mBest�n�@1���ϊ� �V���������̕������� �V���̕ϊ����� �ł���Ƃ��C���� �i�ʉ�1�j---�Q�_�̌������狁�߂� ���� �t�ϊ��̎� �� �Q�_ |
�i�ʉ�2�j---�}��ϐ��\���ŋ��߂� ���� ������t�ϊ��̎� �ɑ������� ����}��ϐ������������ �i�ʉ�3�j---�s��`���ŏ��� �����̕������F �́C���̌`�ɏ����� ������s��ŏ����� �ϊ�����(1)�ɑ������� |
|
�@���ϊ��ɂ�钼���̑�
�y���10.3�z
�i�j�@ (1)�@���ʑS�̂͂ǂ̂悤�Ȑ}�`�Ɉڂ���邩 (2)�@���� (3)�@���� (1) �ɂ�� �ϐ��� (2) ���̕�������}��ϐ��\���ŕ\���� �@�j ����� �ɑ������� �}��ϐ������������ �ϐ��� |
(2) ���̕�������}��ϐ��\���ŕ\���� �@�j ����� �ɑ������� �}��ϐ������������ �ϐ��� �A�j ����� �ɑ������� �ϐ��� ��[#1][#2]�̌��ʂ́C[#1]�Ɛ����I�ɂȂ��Ă���D���Ȃ킿�C���ʑS�̂����� (3) �ϊ��� �V���W�̕����� ����V���W���������ċ����W�̕������ɂ���� |
|
�y���11.1�z
�i���Z���w�T�ɂ�铚�āj�@ ���s���_�����߂� �s���_�̍��W��(x, y)�Ƃ����� ���������� �@�@�s���_�́C ���s�����������߂� �s�������̕��������C �̕ϊ��ɂ��C���������ς��Ȃ����� �@�A�̌W�����r����� ���K�v�\�������ƂȂ� ��� ���� �@�@�s�������� �i�ŗL�l�C�ŗL�x�N�g���C�s���_�C�s�������̊W�j  �i�T�j �O�łȂ������l
�i�T�j �O�łȂ������l
�����̂ŁC�����̕������ς�炸�C���_��ʂ�s�������ɑΉ�����D �i�U�j ���ɁC�ŗL�l �����̂ŁC�e�_ �i�V�j �@�E�}�̂悤�ɁC�ŗL�l �ƂȂ邩��C ���Ȃ��C |
�ŗL������������ �A�j ���C �Ƃ����� ������ �ƂȂ邩��C�_ �}��ϐ� �ȏ�ɂ�� �@�s���_�́C �@�s�������́C �i |
|
�y���11.2�z
�i���Z���w�T�ɂ�铚�āj�@ ���s���_�����߂� �s���_�̍��W��(x, y)�Ƃ����� ���������� �@�@�s���_�́C ���s�����������߂� �s�������̕��������C �̕ϊ��ɂ��C���������ς��Ȃ����� �@�A�̌W�����r����� ���K�v�\�������ƂȂ� ��� �@�@�s�������� |
�i�ʉ��j����ŗL�l�C�ŗL�x�N�g���𗘗p���ĉ��� �ŗL������������ �A�j ���C �Ƃ����� �}��ϐ� |
|
�y���11.3�z
�i�̂݁j�@ �s�������́C �s���_�́C����
�y���11.4�z
�i���Z���w�T�ɂ��j�@ ���s���_�����߂� �䂦�ɁC |
���s�����������߂� �̌`�̕s������������Ƃ���D �������āC���̒����̕����������߂� (1)(2)����v����ɂ� ����āC �����ŁC �s�������̕������́C |
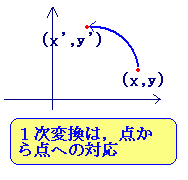
 �@1���ϊ��ɂ���āC���̓_
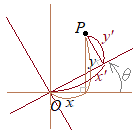
�@1���ϊ��ɂ���āC���̓_ �@�P���ϊ�
�@�P���ϊ�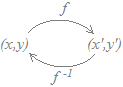 �@�P���ϊ�
�@�P���ϊ�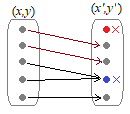 ���C���ʑS�̂��畽�ʑS�̂̏�ւ̎ʑ��m�S�ˁn���P�P�̎ʑ��m�P�ˁn�ł���Ƃ��C�t�ϊ������݂���D
���C���ʑS�̂��畽�ʑS�̂̏�ւ̎ʑ��m�S�ˁn���P�P�̎ʑ��m�P�ˁn�ł���Ƃ��C�t�ϊ������݂���D (2)�ƂȂ��̗�
(2)�ƂȂ��̗�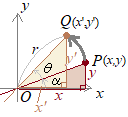 �@���_�𒆐S�Ƃ��Ċe�_���p
�@���_�𒆐S�Ƃ��Ċe�_���p �i�j
�i�j �@���p�����ނQ�ӂ̒�����
�@���p�����ނQ�ӂ̒�����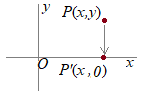 �@�Ⴆ�C�_
�@�Ⴆ�C�_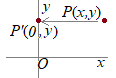 �@���l�ɂ��āC�_
�@���l�ɂ��āC�_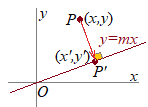 �i����j
�i����j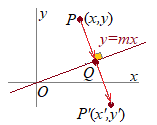 �i����j
�i����j