|
■行列の固有値
A2=
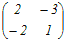 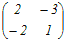 = =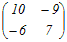 次の固有方程式を解いて,固有値を求める 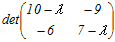 =0 =0(10−λ)(7−λ)−54=0 λ2−17λ+16=0 (λ−1)(λ−16)=0 λ=1, 16 大きい方の固有値は,16 → 4 |
○この頁に登場する【問題】は,公益社団法人日本技術士会のホームページに掲載されている「技術士第一次試験過去問題 共通科目A 数学」の引用です.(=公表された著作物の引用)
○【解説】は個人の試案ですが,Web教材化にあたって「問題の転記ミス」「考え方の間違い」「プログラムの作動ミス」などが含まれる場合があり得ます. 問題や解説についての質問等は,原著作者を煩わせることなく,当Web教材の作成者(<浅尾>)に対して行ってください.
次の固有方程式を解いて,固有値を求める
 =0 =0(8−λ)(λ2+2λ+1)=0 (8−λ)(λ+1)2=0 λ=−1, 8 正であるのはλ=8 → 5 |
|
λが行列Aの固有値であるとき,
固有値λ=1に属する固有ベクトルはdet(A−λE)=0 固有値λに属する固有ベクトルとは, A=λ ⇔ (A−λE)= …(*) となるベクトル (≠)のことをいう. (これに対して,固有値は0となることがあります) ※ が(*)を満たすとき,その定数倍のベクトルも(*)を満たす (*) → (A−λE)(k)= から,固有ベクトルは大きさを除いて定まる. (A−E)= (≠) を満たす. 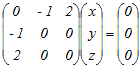 より −y+2z=0, −x=0, 2x=0 ⇔ y=2z, x=0 したがって,tを任意の値(≠0)として x=0, y=2t, z=t ⇔ t 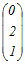 (t≠0)が固有ベクトルとなる. (t≠0)が固有ベクトルとなる.問題文に沿って大きさを1つ選ぶと 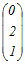 → 2 → 2
|
次の固有方程式を解いて,固有値を求める
 =0 =0(3−λ)(−λ)−4=0 λ2−3λ−4=0 (λ+1)(λ−4)=0 λ=−1, 4 → 4 |
 =0 =0(1−λ)(a−λ)−3a=0 λ2−(a+1)λ−2a=0 λ=4が固有値だから 16−4(a+1)−2a=0 → −6a+12=0 → a=2 λ=−1が固有値だから 1+(a+1)−2a=0 → −a+2=0 → a=2 a=2は両方を満たす → 2 |
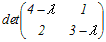 =0 =0(4−λ)(3−λ)−2=0 λ2−7λ+10=0 (λ−2)(λ−5)=0 λ=2, 5 → 4 |
|
平成22年度技術士第一次試験問題[共通問題]
【数学】Ⅲ-20 行列  の固有値は,次のどれか. の固有値は,次のどれか.10, 1, 3 2−1, 1, 3 31, 2, 3 4−3, −1, 0 5−1, 0, 2 HELP  =0 =00 を含む3行目に沿って展開する 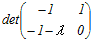 +(−1−λ) +(−1−λ)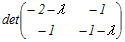 =0 =0(1+λ)+(−1−λ){(−2−λ)(−1−λ)−1}=0 (1+λ)+(−1−λ)(λ2+3λ+2−1)=0 (1+λ)+(−1−λ)(λ2+3λ+1)=0 (1+λ)−(1+λ)(λ2+3λ+1)=0 (1+λ)(1−λ2−3λ−1)=0 (1+λ)(−λ2−3λ)=0 (λ+1)(λ2+3λ)=0 (λ+1)λ(λ+3)=0 λ=0, −1, −3 → 4 |
平成23年度技術士第一次試験問題[共通問題]
【数学】Ⅲ-20 行列 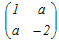 が固有値−3, 2をもつとき,aの値は次のどれか. が固有値−3, 2をもつとき,aの値は次のどれか.1−1または0 2−1または1 3−2または1 4−2または2 5−3または2 HELP 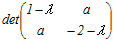 =0 =0(1−λ)(−2−λ)−a2=0 (λ−1)(λ+2)−a2=0 λ2+λ−2−a2=0 λ=−3が固有値だから 9−3−2−a2=0 → a2=4 → a=±2 λ=2が固有値だから 4+2−2−a2=0 → a2=4 → a=±2 a=±2は両方を満たす → 4 |
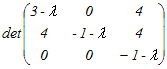 =0 =00 の多い3行目に沿って展開 (−1−λ) 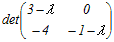 =0 =0(−1−λ)(3−λ)(−1−λ)=0 (λ−3)(λ+1)2=0 λ=3, −1 正の固有値はλ=3 → 3 |

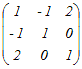



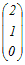
 の固有値は,次のどれか.
の固有値は,次のどれか.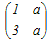
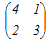
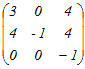 の正の固有値は,次のどれか.
の正の固有値は,次のどれか.