|
■解説 《要約》
○ 同じもの a が p 個,b が q 個,合計 p+q 個あるとき,これらを全部使って1列に並べる順列の総数は 通り ○ 同じもの a が p 個,b が q 個,c が r 個,… ,合計 n 個あるとき,これらを全部使って1列に並べる順列の総数は 通り ※ この公式は,全部使う場合の順列の総数を表わしており,その一部分だけを使う場合の順列の総数を求めるには,それぞれの構成に応じて場合分けして求める必要がある. (解説) 例えば,すべて異なる 5 個の文字 a1a2a3b1b2 を1列に並べる順列の総数は 5P5=5!=120 通りとなるが, それらの中には次のようなものがある. a2a1b1a3b2 a2a3b1a1b2 a3a1b1a2b2 a3a2b1a1b2 さらに, bn を異なるものとして区別し,お互いの位置だけを交換したとき,上の順列は 2! 倍多くなる.
通り になる. これを一般化すると,同じもの a が p 個,b が q 個,合計 p+q 個あるとき,これらを全部使って1列に並べる順列の総数は 通り となって,上の公式が得られる. 3種類以上の文字から成るときも同様. |
例1 a が4個,b が3個,合計7個の文字があるとき,これら全部を1列に並べてできる順列の総数は =35 例2 a が4個,b が3個,c が2個,合計9個の文字があるとき,これらを全部を1列に並べてできる順列の総数は =1260 例3 a が3個,b が2個,c が1個,合計6個の文字があるとき,これらのうち3個を使ってできる順列の総数は (ア)a を3個使うとき aaa の並べ方 → 1 通り (イ)a を2個使うとき aab の並べ方 → =3 通り aac の並べ方 → =3 通り (ウ)a を1個使うとき abb の並べ方 → =3 通り abc の並べ方 → 3!=6 通り (エ)a を使わないとき bbc の並べ方 → =3 通り 計 19 通り ■参考:組合せを用いる解説■ 同じものがあるときの順列の総数は組合せは nCr を用いて解説されることが多いので,これらの関係を示す. aabbb のように同じものを2個と3個含む文字列を並べ替えてできる順列の総数は, 通り であるが,それぞれにおいて a の場所さえ決めれば残りの場所は b に決まる. 例えば abbab では a の番号を1番と4番の2つに決めれば残り2,3,5番は b になる.したがって,aabbb の並べ替え方は,異なる5個の番号札から a の行き先の番号札2個をもらう方法の数 5C2 に等しく,組合せの公式 5C2==10 でも求められる. 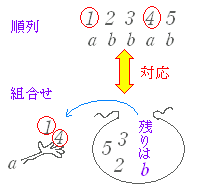 5C3==10
|