|
順路 ■順路の問題 《解説》  【例】
【例】右図のような街路があるとき,A地点からB地点まで最短経路で行く方法は何通りありますか.
順路を式や文字に対応させることができれば取り扱いが容易になります.
A地点からB地点へ,遠回りせずに行く限り,どの順路も東向きに4回,北向きに3回移動していることが分かります.  東に移動することをe(eastの略),北に移動することをn(northの略)で表すと,右の茶色の順路はeneenenに対応しており,青の順路はnneeneeに対応しています.
東に移動することをe(eastの略),北に移動することをn(northの略)で表すと,右の茶色の順路はeneenenに対応しており,青の順路はnneeneeに対応しています.eが4個,nが3個(同じものが)あるときの順列の総数を求めれば,それが順路の総数になります. (答案)  ■ 余談1
■ 余談1右図のように,平行線の幅が異なる場合でも,上の答案でよい:それぞれの順列,例えばenneeneにおいて,はじめのnは御池から丸太町への移動,・・・,はじめのeは西大路から千本への移動,・・・というように意味付けできるからです.
|
■ 余談2
順路の問題を組合せの項目で教えるか,順列の項目で教えるかは,先生しだいです. 筆者は,「同じものがあるときの順列」で教えたほうがよく理解されるという経験則から,順列の項目で教えます.しかし,多くの教科書で順路の問題は「組合せ」の項目にあります.これは,「同じものがあるときの順列」を組合せで説明する方法をとっているからです.
同じものがあるときの順列の総数は組合せ nCr を用いて解説されることが多いので,これらの関係を示す.
aabbb のように同じものを2個と3個含む文字列を並べ替えてできる順列の総数は, 通り であるが,それぞれにおいて a の場所さえ決めれば残りの場所は b に決まる. 例えば abbab では a の番号を1番と4番の2つに決めれば残り2,3,5番は b になる.したがって,aabbb の並べ替え方は,異なる5個の番号札から a の行き先の番号札2個をもらう方法の数 5C2 に等しく,組合せの公式 5C2==10 でも求められる. 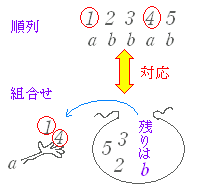 5C3==10 |




 (別解)・・・直接数える場合
(別解)・・・直接数える場合
 (イ)の方法でこの問題を解くときは,例えば右図●印のような検門を通るものを和の法則でまとめます.
(イ)の方法でこの問題を解くときは,例えば右図●印のような検門を通るものを和の法則でまとめます.

 C地点とD地点を通るものを考えます.この場合CD間の道は1通りです.
C地点とD地点を通るものを考えます.この場合CD間の道は1通りです.


 左上の欠けた部分を通る道は,必ずC地点を通ります.また,右下の欠けた部分を通る道は必ずD地点を通ります.そこで,全体から,Cを通るものとDを通るものを取り除きます.
左上の欠けた部分を通る道は,必ずC地点を通ります.また,右下の欠けた部分を通る道は必ずD地点を通ります.そこで,全体から,Cを通るものとDを通るものを取り除きます.


 この問題は,検門を置くほうが扱いやすいでしょう.
この問題は,検門を置くほうが扱いやすいでしょう.