(2)「対応のないt検定」,(A)「元の観測データ有り」,「両側検定」の場合
【例2A.1】
| 男子 | 女子 |
| 7.3 | 8.6 |
| 8.2 | 8.4 |
| 8.6 | 9.5 |
| 7.3 | 7.9 |
| 7.9 | 8.3 |
| 8.1 | 8.5 |
| 7.3 |
|
| 7.0 |
|
| 8.2 |
|
右の表は,男子9人,女子6人,計15人の50m走の時間(秒)を測定した結果とします.
この測定結果から,男女間で50m走の時間に有意差が見られるかどうか,対応のないt検定で判断してください.
「F検定→等分散を仮定したT検定」の2段階で行う場合
===①②③ Excelで計算する場合 ===
①Excel2007 ②Excel2010 ③Excel Onlineでほぼ同じ操作になる
ア)Excelのワークシート関数で行うとき
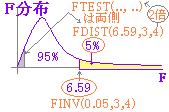
関数FTEST(A群, B群)は,A群とB群の分散の差異が認められない「両側確率」を返す.
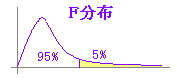
F検定を両側検定で行うと,分散に差異がある場合だけでなく,一致し過ぎる「≒0」場合も検出する.
 しかし,ほとんどのF検定で,分散に有意差があると見なすときは,一致する場合は含めないので,F検定は片側検定で行う.
しかし,ほとんどのF検定で,分散に有意差があると見なすときは,一致する場合は含めないので,F検定は片側検定で行う.
右図のように,片側確率が5%以下であるかどうかを検定するには
FTEST(A群, B群)/2
とするとよい.
結果⇒0.4891..
p値>0.05だから等分散という仮定は棄却されない.
=TTEST(A群, B群, 2, 2)
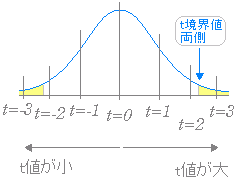
• 第3引数は,片側検定のとき1,両側検定のとき2・・・この問題では,「2」の両側検定を指定
• 第4引数は,t検定の種類を指定する.この問題のような「等分散が仮定できるt検定」の場合は「2」
※なお,前,後というラベルを「含める」「含めない」は両方同じに揃えると自動で判別される.
結果⇒0.019..
p値だけで判断するときは,ここまででよいが,一般的な報告書のようにt値も付けるには
=TINV(上記のp値×2, 自由度)
とする.
結果⇒2.671..
結果をまとめるには,この他に各群の平均と不偏分散[標本の個数N−1で割る方]が必要であるから,=AVERAGE( ), =VAR( )で求めておく.
【結果のまとめ方】
表1は,男子9人,女子6人,計15人の50m走の平均時間(秒)と分散を示したものである.
《表1》 男女の平均時間と標準偏差(秒)
| 男子 | 女子 |
| 平均時間 | 7.766 * | 8.533 * |
| 分散 | 0.305 | 0.282 |
| 人数 | 9 | 6 |
「t検定の結果,男女の平均時間の差は有意であった(両側検定:t(13)=2.671, p=.019).したがって,50m走の時間は男女間で差があると考えられる.」
*p < .05, **p < .01
《初めに等分散の検定を行う》
データ→データ分析→F検定により,次のような表が出力される.
F-検定: 2 標本を使った分散の検定
男子 女子
平均 7.766.. 8.533..
分散 0.305 0.282..
観測数 9 6
自由度 8 5
観測された分散比 1.079..
P(F<=f) 片側 0.489..
F 境界値 片側 4.818..
p値=0.489>0.05だから等分散という仮定は棄却されない
またはF値=1.079<4.818だから等分散という仮定は棄却されない
《次に,等分散を仮定したT検定を行う》
データ→データ分析→t検定:等分散を仮定した2標本・・・により,次のような表が出力される.
t-検定: 等分散を仮定した2標本による検定
男子 女子
平均 7.766.. 8.533..
分散 0.305 0.282..
観測数 9 6
プールされた分散 0.296..
仮説平均との差異 0
自由度 13
t -2.671..
P(T<=t) 片側 0.009..
t 境界値 片側 1.770..
P(T<=t) 両側 0.019..
t 境界値 両側 2.160..
【結果のまとめ方】
ア)と同様に書く
===④ Rで計算する場合 ===
《初めに等分散の検定を行う》
Rで2群の分散を比較する関数 var.test( )の使い方
var.test( x, y, ratio=1, alternative=.., conf.level=..)
• var.test( )の書式で使い,第1,第2引数は必須.2群のデータをベクトルで書く.
• 第3引数以下を省略した場合は,デフォルトで両側検定となる.
• 第3引数以下は,引数の位置ではなく,ratio, alternative, conf.levelなどの名前タグを用いて指定する.
• alternative="two.sided"もしくはalternative="t"により両側検定になる.
• alternative="less"もしくはalternative="l"により,第1引数の分散の方が「小さい」という片側検定を行い、alternative="greater"もしくはalternative="g"により,第1引数の分散の方が「大きい」という片側検定を行う.
• conf.level=0.95により95%の信頼区間が返されるが,これは省略した場合でも既定値となっている.
> boy<-c(7.3,8.2,8.6,7.3,7.9,8.1,7.3,7.0,8.2)
> girl<-c(8.6,8.4,9.5,7.9,8.3,8.5)
> var.test(boy,girl,alternative="greater")
F test to compare two variances
data: boy and girl
F = 1.079, num df = 8, denom df = 5, p-value = 0.4891
alternative hypothesis: true ratio of variances
is greater than 1
95 percent confidence interval:
0.223.. Inf
sample estimates:
ratio of variances
1.079009
p値=0.489>0.05だから等分散という仮定は棄却されない
またはF値=1.079は95%信頼区間0.223~∞に入るから等分散という仮定は棄却されない
《次に,等分散を仮定したT検定を行う》
> t.test(boy,girl,var.equal=TRUE)
Two Sample t-test
data: boy and girl
t = -2.6718, df = 13, p-value = 0.0192
alternative hypothesis: true difference in means
is not equal to 0
95 percent confidence interval:
-1.3865689 -0.1467644
sample estimates:
mean of x mean of y
7.766667 8.533333
p値=0.019<0.05だから平均値が等しいという仮定は棄却される
またはt値=−2.67は95%信頼区間−1.39~−0.147に入らないから平均値が等しいという仮定は棄却される
【結果のまとめ方】
前述と同様
|







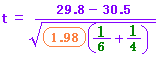 = -0.73
= -0.73


 • Excelワークシート関数のTINV()は両側検定の場合のt値を返すので,この問題のように片側検定のt値を求めるには,確率を2倍しておく(両側で5%の図を片側で5%にする)
• Excelワークシート関数のTINV()は両側検定の場合のt値を返すので,この問題のように片側検定のt値を求めるには,確率を2倍しておく(両側で5%の図を片側で5%にする) しかし,ほとんどのF検定で,分散に有意差があると見なすときは,一致する場合は含めないので,F検定は片側検定で行う.
しかし,ほとんどのF検定で,分散に有意差があると見なすときは,一致する場合は含めないので,F検定は片側検定で行う.