■1 ワークシート関数FREQUENCY()を用いる方法
Excelのワークシート関数FREQUENCY()は、検索範囲と区切りとなる階級値の組が与えられたときに、各々の階級に入るデータの個数(度数)を返す関数です。この関数を正しく利用するには、この関数の特徴についてかなり正確に理解している必要があります。
(*)下の表1のような文字列データ(行ラベル(=生徒番号)が名前であるのは構わないが、通学手段の度数を調べたいときに、この通学手段というデータ(2列目に書かれているデータ)が「バス」などの文字列で記入されているもの)であるときは、FREQUENCY()は利用できません。COUNTIF()を利用する方法など他の頁を見てください。
(*)下の表2,表3のような整数値または実数値の数値データを幾つかの階級に分類したときに、各階級に入る度数を返す関数ですが、FREQUENCY()を利用するためには、ユーザがあらかじめ「階級を区切りを示す数値表」を作成しておかなければなりません。
表2はサイコロを30回投げたときの出た目の回数を記録した生データとします。
○ 表2のような整数の数値データからなる生データをFREQUENCY()を使って集計するには:
(1)あらかじめ 表2Aのように階級表を作っておきます。
○表2A(再掲)
○ この階級表は、区切りとなる値(出た目の欄:縦に並べる)が昇順(小さいものから大きいものへ)に並んでいなければなりません。
| |
A |
B |
C |
D |
E |
| 1 |
試行回数 |
出た目 |
|
出た目 |
回数 |
| 2 |
No.1 |
2 |
|
1 |
9 |
| 3 |
No.2 |
6 |
|
2 |
4 |
| 4 |
No.3 |
1 |
|
3 |
4 |
| 5 |
No.4 |
1 |
|
4 |
4 |
| 6 |
No.5 |
4 |
|
5 |
6 |
| 7 |
No.6 |
5 |
|
6 |
3 |
| … |
… |
… |
|
|
|
| 31 |
No.30 |
1 |
|
|
|
(2)
FREQUENCY()関数を利用するには、下の例では表の で示したセルE2に =FREQUENCY()を書き、そのデータ配列に で示したセルB2:B31を指定し、区間範囲に で示したD2:D7を指定します。
E2に =FREQUENCY(B2:B31,D2:D7) と書きます。
”ここから先が非常に難しい!!”
E3からE7には、E2の数式をコピー・貼り付けしても駄目です。
FREQUENCY()関数は、「配列」(順序を問題にした値の組)として利用しなければならないので、上記のように1つ作ったE2の式を「E2からE7までの配列」にしなければなりません。そのためには、
(I)まず、E2をポイントしておく。
(II)次に、E2〜E7までドラッグして反転表示にする。
(III)Excel画面上端にある数式バー(A,B,Cなどの列見出しの上の白い空白部分=E2をポイントしてときは、=FREQUENCY(B2:B31,D2:D7)と書いてあるのが見える場所)をポイントして、Ctrl+Shift+Enter(CtrlキーとShiftキーを押しながら、Enterキーを1回押す)とします。
|
※ FREQUENCY()関数の階級区切りは160.0≦x<165.0のように使用され、我々には非常に使いにくいものとなっています。しかし、(以下は憶測にすぎませんが)これは欧米文化と日本文化の好みの違いなのかもしれません。例えば、サッカーでU19、U23という場合、各々19歳以下、23歳以下の選手というように区切りとなっている値が下の階級に含まれています。
FREQUENCY()関数で使われている区切り値:19歳 以下、23歳 以下など

日本人好みの区切り値:20歳 以上、25歳 以上など

※上の表のような整数の数値データをFREQUENCY()関数で集計する場合には、E3に返された4という数字は1<x≦2の範囲に入るデータの個数を表しことになりますが、元のデータB2〜B31は整数値なのでこの不等号はまったく働いておらず、 =2 という皮1枚だけでつながっていることになります。
同様にして、E7のセルは5<x≦6の範囲に入るデータの個数すなわち =6 となる個数を表しています。
これに対して、E2のセルはその前のデータがありません(「出た目」という文字列が書かれていて、数値として評価できるものがありません)。このような区切り値の下端では単に、「その値以下」となる個数が返されるようです。
|
○ 表3のような実数(小数)の数値データからなる生データをFREQUENCY()を使って集計するには:
(1)あらかじめ 表3Aのように階級表D2〜D8を(縦に)作っておきます。
× 表3B
| |
A |
B |
C |
D |
E |
| 1 |
生徒番号 |
身長 |
|
階級 |
人数 |
| 2 |
No.1 |
175.1 |
|
160 |
|
| 3 |
No.2 |
182.1 |
|
165 |
|
| 4 |
No.3 |
167.0 |
|
170 |
|
| 5 |
No.4 |
176.7 |
|
175 |
|
| 6 |
No.5 |
168.4 |
|
180 |
|
| 7 |
No.6 |
167.8 |
|
185 |
|
| … |
… |
… |
|
190 |
|
| 51 |
No.50 |
173.3 |
|
|
|
○ 表3A
| |
A |
B |
C |
D |
E |
| 1 |
生徒番号 |
身長 |
|
階級 |
人数 |
| 2 |
No.1 |
175.1 |
|
164.9 |
|
| 3 |
No.2 |
182.1 |
|
169.9 |
|
| 4 |
No.3 |
167.0 |
|
174.9 |
|
| 5 |
No.4 |
176.7 |
|
179.9 |
|
| 6 |
No.5 |
168.4 |
|
184.9 |
|
| 7 |
No.6 |
167.8 |
|
189.9 |
|
| … |
… |
… |
|
194.9 |
|
| 51 |
No.50 |
173.3 |
|
|
|
|

|
表3完成型
| 階級 |
人数 |
| 160.0〜 |
|
| 165.0〜 |
|
| 170.0〜 |
|
| 175.0〜 |
|
| 180.0〜 |
|
| 185.0〜 |
|
または
| 階級 |
人数 |
| 160.0≦x<165.0 |
|
| 165.0≦x<170.0 |
|
| 170.0≦x<175.0 |
|
| 175.0≦x<180.0 |
|
| 180.0≦x<185.0 |
|
| 185.0≦x<190.0 |
|
|
○ この階級表は、区切りとなる値(D列)が 昇順(小さいものから大きいものへ)に並んでいなければなりません。
○ この階級表は、最終的なレポートなどにおいて下の 表3完成型のように書きたくても、FREQUENCY()を使う段階では 表3完成型のように書くと使えません。 (「160〜」や「160.0≦x<165.0」には数字以外のもの(〜や≦,<)が書かれており、このようなセルは数値としては使用できません。このため第1段階でD列の数値データを階級値としてE列に集計し、第2段階で別の列に =E2 のように「値の参照」で自動的に転記することを考えます。)
○【重要:ここが最大の山場】
下の 表3完成型を作るためには、 表3Bではなく、 表3Aのように集計しなければなりません。
というのは、FREQUENCY()関数は「 前の値よりも大きくその値以下となる個数を返す」特徴があるので、 表3B、 表3AのようにD列を記入したとき、
→ 表3BではE2のセルにx≦160となる個数が入り、E3のセルに160<x≦165となる個数が入るため、表3完成型に転記したとき間違った数え方になります。
このようにFREQUENCY()関数には「…よりおおきい…以下」の形で数える特徴があるので、FREQUENCY()関数を使うためにはD列の書き方を工夫します。(※下欄参照)
→ D列に表3Aのように書くと、E列に160.0≦x<165.0の個数が入ります。
【階級表の書き方:要点】 D列には、完成型として予定する階級の上端よりも1目盛り小さい数をその桁数まで書く
| 表3Bの数え方でE2に入る値 |
表3Bの数え方で
E3に入る値 |
E4 |
| … |
159.9 |
160.0 |
160.1 |
… |
164.9 |
165.0 |
165.1 |
… |
169.9 |
170.0 |
表3Aの数え方で
E2に入る値 |
E3 |
E4 |
(2)
FREQUENCY()関数を利用するには、上記の整数の場合と同様、セルE2に =FREQUENCY()を書き、そのデータ配列にB2:B51を指定し、区間範囲にD2:D8を指定します。
⇒ E2に =FREQUENCY(B2:B51,D2:D7) と書きます。
E3からE8には、E2の数式をコピー・貼り付けしても駄目です。
FREQUENCY()関数は、「配列」(順序を問題にした値の組)として利用しなければならないので、上記のように1つ作ったE2の式を「E2からE8までの配列」にしなければなりません。そのためには、
(I)まず、E2をポイントしておく。
(II)次に、E2〜E8までドラッグして反転表示にする。
(III)Excel画面上端にある数式バー(A,B,Cなどの列見出しの上の白い空白部分=E2をポイントしてときは、
=FREQUENCY(B2:B51,D2:D8)と書いてあるのが見える場所)をポイントして、Ctrl+Shift+Enter(CtrlキーとShiftキーを押しながら、Enterキーを1回押す)とします。
(3) 表をレポートなどに使う形にするには:
G列などに階級表を表3完成型の形で書き、H2に =E2 という形で値の参照式を書けばOKです。H3以下は式の単純コピー・貼り付けでできます。
|
※ 数学的に考えると、E3のセルに165.0≦x<170.0となる個数を入れるためには、D2、D3のセルには164.9999···、169.9999···のように書きこまなければならないように思われますが、コンピュータ上の表計算ソフトでは小数は有効数字15桁程度の数字しか扱えません。また、実際に我々が扱うデータは160.3 , 160.07のように小数第何位までで一切られた数になっています。そこで、その桁数で1目盛り小さい数を書けば目的を達成できます ⇒ E3のセルに165.0≦x<170.0となる個数を入れるためには、D2、D3のセルには164.9、169.9と書く。気味が悪いと思えば、164.99、169.99でももちろんOKです。
例えば小数第1位まで書かれたデータでは、165.0≦x<170.0となる数字は、165.0, 165.1 , 165.2 , ··· , 169.8, 169.9 しか登場しないからです。
(一見手品のように見えますが、「東京図書版の数学B」の教科書にも、これとほぼ同じ考え方が紹介されています。)
|
(参考1)
○ この頁で解説したFREQUENCY()関数による度数分布表の作成は、Excelの「分析ツール」からも行うことができます。この場合の階級表作成上の注意点は、この頁で述べたFREQUENCY()関数の特徴と全く同じです。
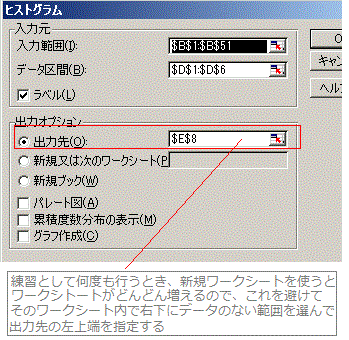
Excel2002では、「ツール」→「分析ツール」→「ヒストグラム」→「入力範囲に生データの数値のみの範囲(1列分だけ)」を(列ラベルも含めるときは「ラベル」にチェック),「データ区間に階級値の範囲」を指定します。Excel2007では、「データ」→「データ分析」→「ヒストグラム」以下同様です。
ただし、FREQUENCY()関数による方法は、ワークシート関数を用いているので参照している生データの値が変更された場合でも、度数分布表は自動的に再計算されます。(Excelの初期設定で、再計算するようになっているとき。なお、FREQUENCY()関数の引数から分かるように、データ数が増減されるときは集計範囲は自動的には更新されません。)
これに対して、「分析ツール」を用いた「ヒストグラム」の作成では、作成時点での生データに対する度数分布が書きこまれるますので、生データの値が変更された場合には、度数分布表は自動的には再計算されません。

|
(参考2)
○ ヒストグラムと棒グラフ
表3のように「理論上は連続的に分布していると考えられる実数値のデータ」を幾つかの階級に分けてできる「度数分布表」をグラフにするときは、通常次の図のように「ヒストグラム」と呼ばれる柱状のグラフで表されます。このような「ヒストグラム」では通常、縦棒の間に隙間がないグラフが用いられます。(値や階級がつながっているという雰囲気がよく出る。)
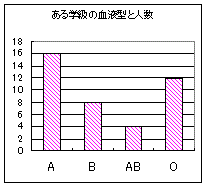
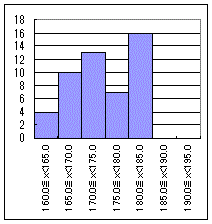 これに対して、いわゆる「棒グラフ」は次の例のように、縦棒の間に隙間があるグラフが用いられるのが普通です。(このように表すとA型とB型などがつながっていないことがよく分かります。また、ヒストグラムでは度数以外に「横軸も数値」であるのに対して、血液型の例では「横軸は名前のラベル」になっている点が違います。)
これに対して、いわゆる「棒グラフ」は次の例のように、縦棒の間に隙間があるグラフが用いられるのが普通です。(このように表すとA型とB型などがつながっていないことがよく分かります。また、ヒストグラムでは度数以外に「横軸も数値」であるのに対して、血液型の例では「横軸は名前のラベル」になっている点が違います。)
|









