|
A , B ���Ɨ��ł���Ƃ��CA �� B ���N����m���� ��P�@����������Q���ĂP��ڂɂR�ȉ��C�Q��ڂɂS�ȉ��̖ڂ��o��m�������߂�Ƃ� �@�����܂łɏK�����l�����ŁC�E���}1�̂悤�ɂP��ځC�Q��ڂ̋N���蓾�邷�ׂĂ̏ꍇ�� N=36 �ƍl����Ƃ��́C�ˁ@���̂悤�ɁCA , B ���Ɨ��ł���Ƃ��CA �� B ���N����m���� |
�}�P
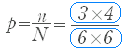 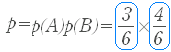 ��� �@���������2����Ƃ��Q��Ƃ������̖ڂ��o��m���� �@�P��ڂɋ���(2 , 4 , 6)���o��m���� �C�Q��ڂɋ���(2 , 4 , 6)���o��m���� |
|||||||||||||||||||||||||||||||||||||||||||||||||
�Ɨ��łȂ����@�ԋʂR�C���ʂQ�������Ă���܂���C�ʂ��P�����o���C���o�����ʂ͌��ɖ߂��Ȃ��ꍇ�ɁC�ԋʂ��Q��o��m�������߂�Ƃ��i�����o�Ƃ����j
�@���o�����ʂ����ɖ߂��Ȃ��ꍇ�́C�P��ڂɋN���������Ƃ͂Q��ڂ̏o���ɉe������F�ˁ@���̂悤�Ɏ��o�����ʂ����ɖ߂��Ȃ��Ƃ��́C�P��ڂ� A ���N���邱�ƂƂQ��ڂ� B ���N���邱�Ƃ͓Ɨ��ł͂Ȃ��D �ˁ@���o�����ʂ����ɖ߂��Ƃ��́C�u�Ɨ��Ȏ��s�̊m���v���K�p�ł��邪�C���o�����ʂ����ɖ߂��Ȃ��Ƃ��́u�Ɨ��Ȏ��s�̊m���v���K�p�ł��Ȃ��D |
�}�Q
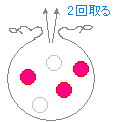 �P��ڂ̋ʂ̏o����5�ʂ�C���̂��ꂼ��ɂ��ĂQ��ڂ̋ʂ̏o����4�ʂ� �� N=20 �ʂ� �@�P��ڂɐԂ��o��̂�3�ʂ�C���̊e�X�ɂ��ĂQ��ڂɐԂ��o��̂͂Q�ʂ� �� n=6 �ʂ� p = = �Ƃ���D ���@���̖��ŁC�P��ڂɎ��o�����ʂ����ɖ߂��Ƃ��i�������o�Ƃ����D�j�́C�P��ڂ̋ʂƂQ��ڂ̋ʂ͂��݂��ɉe�����ꂸ�C�ԐԂƏo��m���� p = �~ = �ŋ��߂���D |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
�P��̎��s�Ŏ��� A ���N����m���� p �̂Ƃ��C���̎��s�� n ��J��Ԃ���A �� r ��N����m���� ���@�T��̂��� A ���R��N����m���Œ��ׂ�ƁC (1)�@AAA �ƂȂ�ꍇ �� pppqq=p3q2 �����łȂ� A ���N���鏇���������قȂ�CA �����v�R��ƂȂ��Ă�����̂͂��ׂē��Ă͂܂�D���̂悤�Ȃ��͉̂E�̂悤��(1)�`(10)��10�ʂ肠�邩��C���̊m���� 10 p3q2 �ɂȂ�D ���@���̌W��10�͎��̂悤�ɂ��ċ��߂���F �A�j�u�������̂�����Ƃ��̏����v�ōl����ꍇ p ���R�Cq(=1 - p) ���Q����Ƃ��C��������בւ��Ăł��鏇��̑����� �ʂ肠�邩��C�C�j�u�g�����v�ōl����ꍇ p ���R�Cq(=1 - p) ���Q����Ƃ��C��������בւ��Ăł��鏇��͕��ѕ��̔ԍ��D�@�A�B�C�D�̂��� p �̍s����̔ԍ��D�R�i�g�����j�Ō��܂�D���@��ʂ� �@�P��̎��s�Ŏ��� A ���N����m���� p �̂Ƃ��C���̎��s�� n ��J��Ԃ���A �� r ��N����m���́Cpr qn - r �ƂȂ�ꍇ���CnCr �ʂ肠�邱�Ƃ���C�����̍��v�� |
�i�T��̂����R��N����m���j �@���� A ���N����m���� p �̂Ƃ��C���̎��s�� 5 ��J��Ԃ��� A �� 3 ��N����m���́C���̊e�ꍇ�𑫂��悢�D�@ (2)�@ppqpq=p3q2 (3)�@ppqqp=p3q2 (4)�@pqppq=p3q2 (5)�@pqpqp=p3q2 (6)�@pqqpp=p3q2 (7)�@qpppq=p3q2 (8)�@qppqp=p3q2 (9)�@qpqpp=p3q2 (10) qqppp=p3q2 ���W���ɂȂ��āC�a�� 10 p3q2 �ɂȂ�D ��� �@�d�݂�5����Ƃ��\�����傤��3��o��m���� �@�P��̎��s�ŕ\���o��m���� p = �C�\���o�Ȃ��m���� q=1 - p = ��������� �@���������6����Ƃ��P�̖ڂ����傤��2��o��m���� �@�P��̎��s�łP�̖ڂ��o��m���� p = �C�P�̖� |