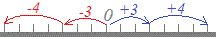|
← PC用は別頁
≪絶対値≫■ 絶対値とは ○ 以下の2つの定義(1)(2)は、同じことを表しています。
初めて学ぶ人は、一応どれも「聞いたことがある」程度にしておいて、実際に自分が問題に向かうときは一番分かりやすい定義を使うとよいでしょう。 中学生には(2)分かりやすいと考えられます。 (1) 中学校の教科書に書かれている「絶対値」の定義
正負の数の「絶対値」とは、数直線上で「原点からある数までの距離」のことをいいます。
例
−4の絶対値は4です。 +3の絶対値は3です。 ただし、0の絶対値は0とします。  「絶対」という言葉の魔術的雰囲気(「絶対に正しい」とか「他の物に左右されない絶対的な存在」といった雰囲気)に惑わされて、難しく考えてはいけません。英語のabsolute valueを直訳したら「絶対値」という用語になるというだけのことです。
【重要】
距離は向き(符号)を考えずに「間の長さ」だけで考えますので、0以上になります。 だから、元の数が「正の数」であっても「負の数」であっても、原点からの距離で定義される「絶対値」は0以上の値になります。 |
|
【例1】
(解答)5+5の絶対値は 
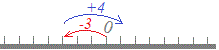
【例2】
(解答)1.3−1.3の絶対値は 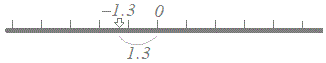
【例3】
(解答)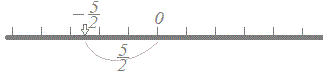 |
|
◎(2) 見た目で考える「絶対値」の定義
正負の数は−4、+3のように「符号の部分」と「数字の部分」で書かれています。(正の数の符号+は省略することがあります。)
このとき、「絶対値」とは、「符号の部分」を取り除いた「数字の部分」のことをいいます。 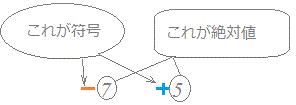
例
−7の絶対値は7です。 +5の絶対値は5です。 −1.4の絶対値は1.4です。
+の絶対値はです。
ただし、0の絶対値は0とします。
|
|
≪問題1≫ 次の各問について、正しいものを下の選択肢から選んでください。(正しい選択肢をクリック)
(1)
+5 の絶対値は
−5 ,
5 ,
±5
(2)
−8の絶対値は
−8 ,
8 ,
±8
(3)
絶対値が4になる数は
−4 ,
4 ,
±4
|
|
≪問題2≫ 次の各問について、正しいものを下の選択肢から選んでください。(正しい選択肢をクリック)
(1)
−5の絶対値と−4の絶対値とではどちらが大きいですか
−5 ,
−4
−5の絶対値は5
−4の絶対値は4だから −5の絶対値の方が大きい.
※「−5は−4よりも小さい.」
「−5の絶対値は−4の絶対値よりも大きい.」 これらはいずれも正しいが,別の話である.
(2)
−8の絶対値と7の絶対値とではどちらが大きいですか
−8 ,
7
(3)
絶対値が3よりも小さい整数は何個ありますか.
1個,
2個,
3個,
4個,
5個
(4)
絶対値が3以上で4以下になる整数は何個ありますか
1個,
2個,
3個,
4個,
5個,
(5)
次の内で絶対値が最も大きい数はどれか
(6)
次の内で最も小さい数はどれか |
|
※絶対値を求めるときに注意すべきこと (+5)+(−3) や (−7)+(+4)−(−6)のように、正負の数の足し算、引き算で表される数の絶対値は、それぞれの数の絶対値の足し算や引き算になるとは限りません。(等しい場合も等しくない場合もあります。) 例
(+5)+(−3)=2だから(+5)+(−3)の絶対値は2です。
⇒ これは、(+5)の絶対値5と(−3)の絶対値3を足したもの8とは等しくなりません。 ⇒ (+5)+(−3)の絶対値 ≠ 5+3
(+5)+(+3)=8 や (−5)+(−3)=−8のように同符号の数を足した数の絶対値は、それぞれの絶対値を足したものと等しくなります。
⇒ (+5)+(+3)の絶対値 = 5+3
■ 中学校では、「値を求めてから、絶対値を考えるとよい」
びっくりするほど簡単な話!
 |
|
≪問題3≫ 次の各問について、正しいものを下の選択肢から選んでください。(正しい選択肢をクリック)
(1)
(+3)+(−8) の絶対値は
−11 ,
11 ,
−5 ,
5
(2)
(−4)+(−3)の絶対値は
−7 ,
7 ,
−1 ,
1
|