|
=== �ǎ҂��z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
�y���1�z
�i����j�@��ϕ� �i2011�N�x��B���ȑ�j
����Βl�t�����̐ϕ������߂�ɂ́C�u�ꍇ�����ɂ���Βl���O���Ă���ϕ�����v�̂���{
���w�C���Ɂx�w�Ɂx���ׂ���������҂������ ���u�y�ȕ��@�v�u�ߓ��C���Z�v�͂Ȃ���������̎��Ԃ����� 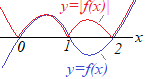
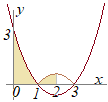
������ �̃O���t�͉E�}�̒ʂ�D �A�j−1��x<0�̂Ƃ� �C�j0��x<1�̂Ƃ� �E�j1��x<2�̂Ƃ� �A)�C)�E�j��� |
�i�Ւk�j
���Z���w�T�C�U�̓��ĂŁC�ꍇ�����́u�R��Ȃ��v�u�d���Ȃ��v�s���̂���{�ŁC�u�d��������v�悤�ȏꍇ�����́C�߂����ɂȂ����C��ϕ��ɂ��Ă� �Ƃ����u�d�v�����v�Ɏ������悤�ɁC�Ȃ��ڂ�c�́C���ɂ��E�ɂ������Ă���D 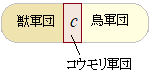 ���Ȃ킿
���Ȃ킿
�A�j a��x��c�̂Ƃ�f(x)=f1(x)
�̂悤�ɏ�����C�R�E�����R�cc�́C�����̋�Ԃɂ��C�E���̋�Ԃɂ������Ă��邱�ƂɂȂ�D�i���ȏ���Q�l���ł́C�A�j�C�j�̂悤�ɏ������D�j�C�j c��x��b�̂Ƃ�f(x)=f2(x) �@�������C���̌���������̂ŁC���ʓI�ɂ́C�����͂Ȃ��D ����ɂ�� a��x<c c��x��b
�Ƃ������߂��ł���I �i�y���y���̔���P���͂����Ɓi |
|
�y�ޑ�1.1�z�@
�@��ϕ�
�m������n�i2016�N�x�k�C�w���� �H�w���j
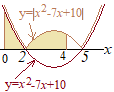
������ �A�j 0��x��2�̂Ƃ� �C�j 2��x��4�̂Ƃ� �A�j�C�j��� 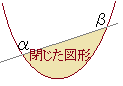 �i�Ւk�j
�i�Ւk�j�@�Ԉ���āu�U���̌����v���g��Ȃ��悤�ɁI �@������u�U���̌����v���g����̂́C�E�}�̂悤�Ɂu��_�����_�܂ł̕����}�`�v�ɂȂ��Ă���ꍇ�Ɍ���! �@�ޑ�1�́C�����}�`�łȂ�����u�U���̌����v�͎g���Ȃ��D |
�y�ޑ�1.2�z�@
�@��ϕ�
�m������n�i2005�N�x�b��嗝�H�w���j
|
|
�y�ޑ�1.3�z�@
�@��
�m������n(1)�@������f(x)=0�̉������߂�D (2)�@��y=f(x)�̃O���t�������D (3)�@��y=f(x)�̃O���t��x���Ƃň͂܂ꂽ�����̖ʐς����߂�D �i2016�N�x�V����j
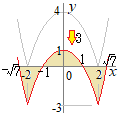 (1)
(1)(2)�@�E�}�i�Ԑ��j (3) ���E�Ώ̂�����x��0�̕����̖ʐς����߂āC�Q�{���� �A�j 0��x<1�̂Ƃ� �C�j 1��x<2�̂Ƃ� �E�j 2��x< �A�j�C�j�E�j��� |
�y�ޑ�1.4�z�@
�@xy���ʏ�ŁCy=x�̃O���t��
�m������n�i2011�N�x���s�嗝�Ȍn�j
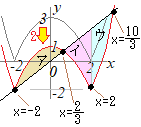
−2��x<2�̂Ƃ�
y=x�Ƃ̌�_��
�A�j−2��x<
���̌v�Z�́C�u������U���̌����v�łł���D �C�j
�E�j2��x�̂Ƃ�
y=x�Ƃ̌�_�� �A�C�E�j��� |
|
�y���2�z
�i����j�i2005�N�x����c�古�w���j
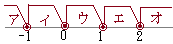 �������̐�Βl�L����
�������̐�Βl�L�����O���ɂ� �ˁ@���ڂ���ׂāC�ׂ����ꍇ�������� ������ �A�j−2��x<−1�̂Ƃ� �C�j−1��x<0�̂Ƃ� �E�j0��x<1�̂Ƃ� �G�j1��x<2�̂Ƃ� �A�C�E�G�j��� |
�y�ޑ�2.1�z�@
�@��f(x)��
�m������n(1) f(x)�̐�Βl�L�����͂����D (2) y=f(x)�̃O���t�������D (3) y=f(x)�̃O���t�� �i2016�N�x������@�w���j
(1)
�A�j �C�j �E�j �G�j �I�j (2) 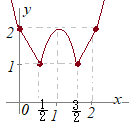 �O���t�͉E�}�̒ʂ�
�O���t�͉E�}�̒ʂ�(3) �}�`��x=1�Ɋւ��đΏ̂�����Cx��1�̕����̖ʐς����߂ĂQ�{���� 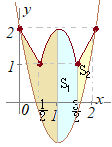
|
|
�y���3�z
�@1��x��2�Ƃ���D�� �i2016�N�x���Q��_�w���E����w���j
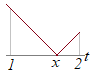 �i����j
�i����j�A�j1��t<x�̂Ƃ��Ct−x<0������ |t−x|=x−t �C�jx��t<2�̂Ƃ��Ct−x>0������ |t−x|=t−x |
|
|
�y�ޑ�3.1�z�@
�@0<k<3�̂Ƃ��C����y=kx�ƋȐ�y=|x(x−3)|�Ƃň͂܂ꂽ�}�`�̖ʐς��ŏ��ƂȂ�悤��k�̒l�����߂�D
�m������n�i2005�N�x�����w�|��j
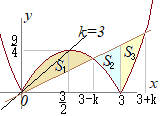 �A�j 0��x<3�̂Ƃ��C
�A�j 0��x<3�̂Ƃ��C|x(x−3)|=−x(x−3)������ −x(x−3)=kx�Ȃ�� x(x−k+3)=0 x=0, 3−k �C�j 3��x�̂Ƃ��C |x(x−3)|=x(x−3)������ x(x−3)=kx�Ȃ�� x=3+k (��3) �Ƃ�����
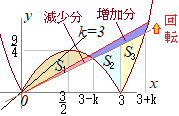 �i�Q�l�j�ŏ��ƂȂ�ꍇ�C�E�}�̑������ƌ��������������Ȃ�D
�i�Q�l�j�ŏ��ƂȂ�ꍇ�C�E�}�̑������ƌ��������������Ȃ�D��`�̖ʐς́i���S�p�������Ȃ�j���a�̂Q��ɔ�Ⴗ�� �@�����w�Z�ŏK���������}�`�̐����ɂ��COQ:OP=(3+k):(3−k) |
�y�ޑ�3.2�z�@
�@f(x)��
�m������n�������Cx��0�Ƃ���D �@��y=f(x)�̃O���t��x���Cx=1, x=4�ň͂܂�� �����̖ʐς� �i �@�@ �j �@�@ �ł���D �i2016�N�x����c��l�ԉȊw���j
|
|
�y�ޑ�3.3�z�@
(1)�@a��C�ӂ̎����Ƃ���Ƃ��Cy=x|a−x|�̃O���t�������D
�m������n(2)�@ �i2005�N�x�����͂����Ė�����j
(1)
�A�j�@x<a�̂Ƃ��Cy=x(a−x) �C�j�@a��x�̂Ƃ��Cy=x(x−a) a<0�̂Ƃ��}1�Ca=0�̂Ƃ��}2�C0��a�̂Ƃ��}3 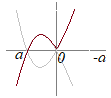 �|�}1�| 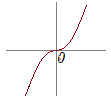 �|�}2�| 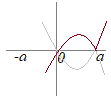 �|�}3�| (2) �@(1)�ɂ����āCa=1�̏ꍇ���l����� �A�j�@x<1�̂Ƃ��C−1��t��x (<1)�ł���ǂ�t�ɂ��Ă��Ct<1�����藧���� �C�j�@1��x�̂Ƃ� −1��t<1�ł���ǂ�t�ɂ��Ă��Ct<1 1��t��x�ł���ǂ�t�ɂ��Ă��C1��t�ł��邩�� �A�j�̏ꍇ�C �C�j�̏ꍇ�C
|
�y�ޑ�3.4�z�@
0<t<1����t�ɑ�,
�m������n�Ƃ����D���̂Ƃ��C���̐ݖ�ɓ�����D (1)�@f(t)�����߂�D (2)�@f(t)���ŏ��ɂ���t�̒l�����߂�D �i2005�N�x���R���ȑ�j
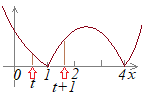 (1)
(1)0<t<1<t+1<2������ �i�r���v�Z���j (2) �̉��́C 0<t<1������
|
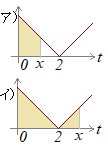 �A�j
�A�j 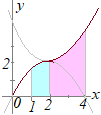 �@�E�}�̖ʐς�
�@�E�}�̖ʐς�