|
【曲線で囲まれた図形の面積】
（解説）区間a≦x≦bにおいて，つねにf(x)≧g(x)であるとき，２つの曲線y=f(x), y=g(x)と直線x=a, x=bとで囲まれる図形の面積は S={ f(x)−g(x) }dx …(1) ※ （上）−（下）の積分 と考える ■ この公式は，広く適用できるもので，右図のＢ，Ｃのように２つのグラフy=f(x) , y=g(x)が両方ともx軸よりも上にある場合や，両方とも下にある場合だけでなく，Ａのようにx軸を横切っている場合でも成り立つ． ■ 教科書では，通常，右図２のような図形の面積を S=f(x)dx と覚えることになっているが，これは（上）がy=f(x)で，（下）がx軸すなわちy=0という特別な場合に過ぎないから， S={ f(x)−0 }dx=f(x)dx となって，上記の公式(1)に含まれている． ■ また，右図３のような図形の面積は（上）がx軸すなわちy=0で，（下）がy=f(x)という特別な場合に過ぎないから， S={ 0−f(x) }dx=−f(x)dx となって，この場合も上記の公式(1)に含まれている．
要するに公式(1)で全部行ける
■ ただし，図４のようにx軸よりも上の部分と下の部分があるときに，y=f(x)とx軸，直線x=a, x=cで囲まれた図形の面積は
f(x)dx…(*)
では求められないことに注意．右図４のように，区間によって上にある関数と下にある関数が入れ替わっている場合は，区間ごとに分けて面積を求める必要がある． ○正しくは→{ 0−f(x) }dx+{ f(x)−0 }dx =−f(x)dx+f(x)dx とすべきところを，上の(*)の計算は ×間違って→f(x)dx =f(x)dx+f(x)dx で計算してしまっているので，区間a≦x≦bの面積の符号を逆にしてしまっており，図４のような図形の場合に，（＋）の部分と（−）の部分の面積が打ち消し合って，何も求められない． ■ 図５のようにy=f(x)とy=g(x)が上になったり下になったりしている場合に，区間a≦x≦dにおいてこれらの曲線で囲まれた図形の面積を求めるためには S={ g(x)−f(x) }dx+{ f(x)−g(x) }dx +{ g(x)−f(x) }dx…(*1) のように，どちらが上になるかに応じて「ていねいに区間を分けて計算する」ことが重要
公式(1)で全部行けるが，実際の計算は，上下を確かめて，ていねいに区間に分けて行うことが重要
|
図１
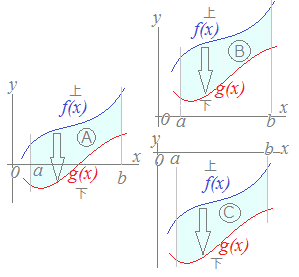 図２図３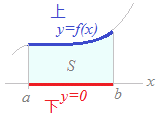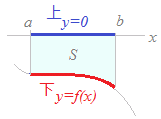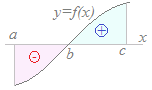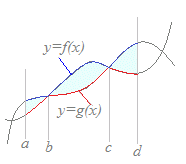    
教科書や参考書では，上の図５の図形の面積を
S=| g(x)−f(x) |dx…(*2)
と書く場合があるが，このような絶対値記号を付けたままでは筆算はできず，結局(*1)の形に直す必要がある．（絶対値記号で表したものは，内容的に正しいが，それを筆算で数値に直すのは無理）
特に，(*2)は |{ g(x)−f(x) }dx|や |g(x)|dx−|f(x)|dxとは 等しくないことに注意 |
|
【例１】･･･図１に対応する問題
（解答）区間0≦x≦2において，y=x+1, y=x2−1で囲まれる図形の面積を求めてください． グラフの概形（だいたいの形）を描いて，どちらが上にあるか調べる
⇒ 図のようになるから，0≦x≦2において，y=x+1が上にあることが分かる
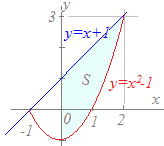S={ (x+1)−(x2−1) }dx
=(−x2+x+2)dx
=−++2x
=(−+2+4)−(0)=
※初歩的な注意として，（上）−（下）で計算している限り，x軸よりも下にある部分の面積は特別扱いしなくても計算に入っていることに注意 |
【例２】･･･図２に対応する問題
（解答）区間0≦x≦2において，y=x2−2x+1とx軸で囲まれる図形の面積を求めてください． グラフの概形（だいたいの形）を描いて，どちらが上にあるか調べる
⇒ 図のようになるから，0≦x≦2において，y=x2−2x+1がx軸よりも上にある
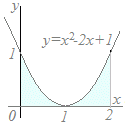S=(x2−2x+1)dx
= −x2+x
=(−4+2)−(0)=
|
|
【例３】･･･図３に対応する問題
（解答）区間−1≦x≦1において，y=(x+1)2(x−1)とx軸で囲まれる図形の面積を求めてください． グラフの概形（だいたいの形）を描いて，どちらが上にあるか調べる
⇒x軸とx=−1で接し，x=1で交わり，xがさらに大きくなると正の値を取る．
図のようになるから，−1≦x≦1において，y=(x+1)2(x−1)がx軸よりも下にある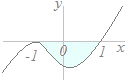 
S=−(x+1)2(x−1)dx
被積分関数を展開する=(−x3−x2+x+1)dx
奇関数，偶関数を
=(−x2+1)dx−a≦x≦aで積分する場合 x dx=0 x3 dx=0 …… C dx=2C dx x2 dx=2x2 dx …… =2(−x2+1)dx =2−+x = ≪別解≫ S=−(x+1)2(x−1)dx S=−[ (x+1)2{ (x+1)−2 } ]dx =−{ (x+1)3−2(x+1)2 }dx =−+2 =(−4+)−(0)= |
≪微分の公式≫と≪不定積分の公式≫
○基本公式
xndx=+C…(A)
○発展公式
(ax+b)ndx=+C…(B)
(B)の公式は，普通は数学IIIで習い，合成関数微分法（⇔置換積分法）で簡単に示せる．数学II（と数学B）の範囲でも示せるが長くなるので，発展問題にしばしば出遭う場合には，(B)を公式として覚えてしまう． この(B)の公式を使うと，さらに次のような変形によって計算が楽になる⇔計算間違いが減る．
次数の高い方
(x+a)2(x+b)dx(x+a)2 に勝たせてしまう． 次数の低い方 (x+b) は解体して吸収されてしまう． =(x+a)2{ (x+a)+(b−a) }dx =(x+a)3dx+(b−a)(x+a)2dx =+(b−a)+C
※ 数学IIの問題として(B)の公式を使わなければできない問題を出題すると，学習指導要領の範囲を逸脱したものとなる．したがって，「普通の方法でもできる」が，「裏技を使えばより簡単になる」という形の問題にだけ適用できる．
ただし，(B)の公式を使えば計算が簡単になり，計算間違いが減るといっても，分母にaが着くということを忘れると，逆に計算間違いになるので，公式(B)を使う場合は正確に覚えておく必要がある． |
|
【例４】･･･図５に対応する問題
（解答）y=1−x2，y=−x−1，２直線x=−2 , x=2で囲まれる図形の面積を求めてください． グラフの概形（だいたいの形）を描いて，どちらが上にあるか調べる
⇒1−x2=−x−1を解いて交点のx座標を求めると
x=−1 , 2 図のようになるから， −2≦x≦−1において−x−1≧1−x2 −1≦x≦2において−x−1≦1−x2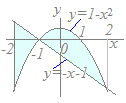 
S={ (−x−1)−(1−x2) }dx
+{ (1−x2)−(−x−1) }dx
=(x2−x−2)dx
+(−x2+x+2)dx
=−−2x+−++2x
･･･気長に計算する･･･
=
|
【例５】･･･図５の下の(*2)に関連する問題
|x2+x−2|dxを求めてください．
（解答）※このような問題を解くには，ていねいに場合分けして，| |記号を外してから積分計算を行う．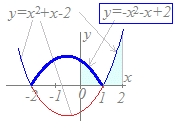 
x2+x−2=(x+2)(x−1)=0の解はx=−2, 1だからx<−2, x>1のとき x2+x−2>0 −2<x<1のとき x2+x−2<0 したがって x<−2, x>1のとき |x2+x−2|=x2+x−2 −2<x<1のとき |x2+x−2|=−x2−x+2 |x2+x−2|dx=(−x2−x+2)dx +(x2+x−2)dx ･･･気長に計算する･･･
=3
|
|
【例６】･･･右の公式に対応する問題
（解答）y=−2x2−x+1とy=x2+2x−2で囲まれる図形の面積を求めてください． グラフの概形（だいたいの形）を描いて，どちらが上にあるか調べる ⇒ 右図下のような図形になり，２交点の間では，y=−2x2−x+1が上にある．
２交点を求める （上）−（下）=−3x2−3x+3 ⇒ −2x2−x+1=x2+2x−2を解くと
S=(−3x2−3x+3)dx
={ −3(x−α)(x−β) }dx
=−(β−α)3
=()3=
α=, β=
この問題を，基本に忠実に
S=(−3x2−3x+3)dx =−x3−x2+3x によって計算するのは大変． x3にx=を代入する計算などが，とても煩わ しいので，話を単純化して
計算が大変→計算間違いが起りやすい
を合言葉に，右の公式も覚えておく値打がある．
計算が簡単→計算間違いが起りにくい |
≪放物線や直線で囲まれた図形の面積≫ ･･･「交点から交点までの積分」になるとき
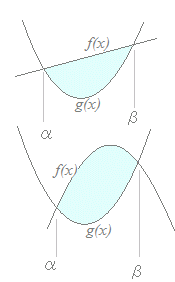右図の上は，y=f(x)=x+2とy=g(x)=x2 のように直線と放物線で囲まれた図形になる． この図形の面積を，求めるには { f(x)−g(x) }dx =(−x2+x+2)dx のように，２交点を積分区間の下端と上端として，２次関数の積分を行う． この定積分は，−x2+x+2=0の２つの解がα=−1, β=2だから { −(x−α)(x−β) }dxの形に 書ける． また，右図の下は，y=−2x2−x+1とy=x2+2x−2のように２つの放物線で囲まれた図形になる． この図形の面積を，求めるには { f(x)−g(x) }dx=(−3x2−3x+3)dx のように，２交点を積分区間の下端と上端として，２次関数の積分を行う． ただし，** , ##には，−3x2−3x+3=0の２つの解 α=, β=…($$) が入ります． この面積も { −3(x−α)(x−β) }dxの形に書ける． このような場合に，次の公式が利用できます．
ax2+bx+c=0の２つの解をα, β (α<β)とするとき
この公式を使えば，α, βの値が($$)の例のような複雑な分数かつ根号であってもβ−α=となるので，簡単に代入できる．
{ ax2+bx+c }dx =a(x−α)(x−β)dx =−(β−α)3 が成り立つ． |
|
≪ここまでに登場した公式一覧≫
【曲線で囲まれた図形の面積】
区間a≦x≦bにおいて，つねにf(x)≧g(x)であるとき，２つの曲線y=f(x), y=g(x)と直線x=a, x=bとで囲まれる図形の面積は S={ （上）−（下） }dx …(1)
【奇関数，偶関数を−a≦x≦aの区間で積分する場合】
（奇関数）dx=0 …(2) （偶関数）dx=2（偶関数）dx …(3)
【(ax+b)nの不定積分】
(ax+b)ndx=+C …(4) |
【(x+a)2(x+b)の積分】
次数の高い方 (x+a)2に勝たせて，次数の低い方(x+b)を吸収する． (x+a)2(x+b)dx =(x+a)2{ (x+a)+(b−a) }dx =(x+a)3dx+(b−a)(x+a)2dx …(5)
【放物線の２交点間で積分するとき】
（解説）a(x−α)(x−β)dx=−(β−α)3 …(6) (6)の公式は，２次方程式の解と係数の関係を利用して示すこともできるが，(5)の応用として示すこともできる． a(x−α)(x−β)dx=a(x−α)(x−α+α−β)dx =a{ (x−α)2+(α−β)(x−α) }dx ここで公式(4)を使うと =a(x−α)3+(α−β)(x−α)2 =a[ { (β−α)3+(α−β)(β−α)2 }−{ 0+0 } ] =a{ (β−α)3−(β−α)3 } =−(β−α)3 |
|
※正しい選択肢の番号をクリックしてください．
なお，暗算ではできませんので，別途計算用紙と筆記用具が必要です． |
はじめにグラフの概形を描く
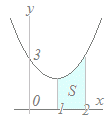y=x2−2x+3=(x−1)2+2と変形できるから，頂点の座標は(1,2)グラフは右図のようになり，1≦x≦2の区間でx軸よりも上にある． （上）−（下）=(x2−2x+3)−(0) =x2−2x+3 S=(x2−2x+3)dx={ (x−1)2+2 }dx =+2x=(+4)−(0+2)= |
|
はじめにグラフの概形を描く（極値までは求めなくてもよい）
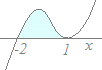y=0となるのはx=−2, x=1のときで，x=−2でx軸と交わりx=1でx軸と接し（重解形） それよりも大きくなるとy>0になるから グラフは右図のようになり，−2≦x≦1の区間でx軸よりも上にある． （上）−（下）=(x−1)2(x+2)−(0) =(x−1)2(x+2)=x3−3x+2 S=(x−1)2(x+2)dx=(x−1)2(x−1+3)dx ={ (x−1)3+3(x−1)2 }dx =+(x−1)3=(0)−(−27)= |
|
|
はじめにグラフの概形を描く（極値までは求めなくてもよい）
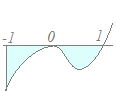y=x2(x−1)と変形できるからy=0となるのはx=0, x=1のときで，x=0でx軸と接し（重解形） x=1でx軸と交わり それよりも大きくなるとy>0になるから グラフは右図のようになり，−1≦x≦1の区間でy≦0 （上）−（下）=(0)−(x3−x2) =−x3+x2 =(−+)−(−−)=→2 ［計算間違い防止：別ルート探索…(2)(3)で検算］ S=(−x3+x2)dx において，積分区間が−1≦x≦1だから(2)(3)の性質が使える． x3は奇関数 → 0になって消える x2は偶関数 → 右半分の２倍と同じ S=2x2dx=2= |
|
|
はじめにグラフの概形を描く（極値までは求めなくてもよい）
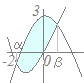y=x2+2x=x(x+2)はx=−2 , 0でx軸と交わり，下に凸y=−x2+3は(0, 3)でy軸と交わり，上に凸 グラフは右図のようになり，２つの交点の間でy=−x2+3が上にある （上）−（下）=(−x2+3)−(x2+2x) =−2x2−2x+3
−2x2−2x+3=0 → 2x2+2x−3=0
S=(−2x2−2x+3)dx=−2(x−α)(x−β)dx解の公式を用いて解くと x= → α= , β=とおく α,βの値を直接代入するのは煩雑な計算になるので，公式(6)を使う．（β−α=を利用する） S=−(β−α)3=→5 |
|
≪自由研究１≫
結果は次の式を機械的に計算し，小数第3位までの小数で示します．
S=|y2−y1|dx
（例：10/3=3.333）
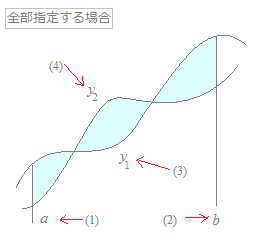
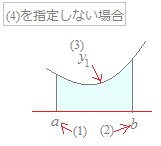
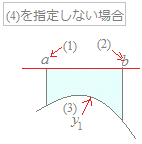
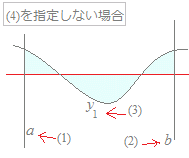
右図のような面積を計算します．
(1)(2)は必須です．ただしa<bとします． (3)(4)で空白があれば自動的に0と見なします． (3)(4)のどちらが上にあるか，途中で上下が入れ替わるかなどは，コンピュータが判断して| |で計算します． 分数は2/3, -1/3のように記入してください．
≪面積≫
（参考） |
   
|
|
≪自由研究２≫
結果は次の式を機械的に計算し，小数第3位までの小数で示します．
S=|ax2+bx+c|dx=(β−α)3 ←(6)
（例：10/3=3.333）
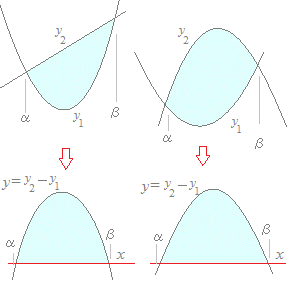
右図のような面積を計算します．
２つの曲線で囲まれる部分の面積を求めたいときは，かわりにy2−y1を求めて，その係数を入力してください． 積分区間の下端と上端α, βは自動で計算します． x2の係数は0であってはいけません．残りの欄は空白があれば自動的に0と見なします． 分数は2/3, -1/3のように記入してください．
≪面積≫
|
|
|
≪自由研究３≫
結果は次の式を機械的に計算し，小数第3位までの小数で示します．
S=|y|dx+|y|dx
（例：10/3=3.333）
右図のような面積を計算します．
２つの曲線で囲まれる部分の面積を求めたいときは，かわりにy2−y1を求めて，その係数を入力してください． 右図のようにα≦β≦γの順に並べてください．２つ目，３つ目の図のように重解形になる場合は，α=β<γとかα<β=γのように２つの値を等しく指定してください 先頭の係数は0であってはいけません． 分数は2/3, -1/3のように記入してください．
≪面積≫
|
高校生の初歩的な質問として，どう書けばxという因数自体を表せるのか分からない，というのがあります．
⇒ xを因数とするには，x−0のように記入してください． |
|
≪類題：問題と答≫ 1. ==== 右図の形になるもの ====
積分区間の
下端（左端）と上端（右端） x=a, x=b が与えられていて， 曲線y=f(x)≧0とx軸 で囲まれた図形の面積を求める問題
|
2. ==== 右図の形になるもの ====
積分区間の
下端（左端）と上端（右端） x=a, x=b が与えられていて， 曲線y=f(x)≦0とx軸 で囲まれた図形の面積を求める問題
| ||||||||||||||||||||||||||||
3. ==== 右図の形になるもの ====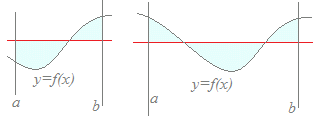
積分区間の
下端（左端）と上端（右端）x=a, x=b が与えられていて， 曲線y=f(x)とx軸 で囲まれた図形（x軸の上側も下側もある場合）の面積を求める問題
|
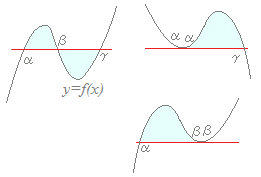
4. ==== 右図の形になるもの ====
曲線y=f(x)とy=g(x)
の交点（接点）α,β,γを各自で求めて， y=f(x)とy=g(x)で囲まれた図形の面積を求める問題  f(x) , g(x)が２次式と1次式，または２次式と２次式の組合せの場合 （上）−（下） =a(x−α)(x−β)の形になるので a(x−α)(x−β)dx =−(β−α)3 …(6) の公式が使える．
|
||||||||||||||||||||||||||||
5. ==== 右図の形になるもの ====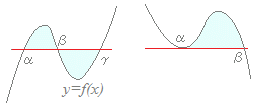 
曲線y=f(x)とx軸
の交点（接点）α,β,γを各自で求めて，y=f(x)とx軸で囲まれた図形の面積を求める問題（区間に応じて，引き方を変える．(6)のような簡単な公式にはならない．）
|
6. ==== 右図の形になるもの ==== 
曲線y=f(x)とy=g(x)
の交点（接点）α,β,γを各自で求めて， y=f(x)とy=g(x)で囲まれた図形の面積を求める問題 f(x) , g(x)が３次式と1次式，または３次式と２次式の組合せの場合 （上）−（下） =a(x−α)(x−β)(x−γ)と=−a(x−α)(x−β)(x−γ)の形になるので，グラフの形を考えて a(x−α)(x−β)(x−γ)dx−a(x−α)(x−β)(x−γ)dx などを計算します．(6)のような簡単な公式にはならない．
|
...メニューに戻る