■解説
●成分がすべて0である行列を零行列といい,型を混同するおそれがなければすべてOで表します。
2次正方行列の零行列は 0=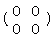 , ,
3次正方行列の零行列は 0=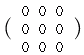 です。 です。
●正方行列のうち対角成分(ここでは主対角線上の成分:行番号と列番号が同じもの)が1で,他の成分が0となる行列を単位行列といい,型を混同するおそれがなければすべてEで表します。
2次の単位行列は E=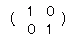 , ,
3次の単位行列は E= です。 です。
|
※ 以下は,2次の正方行列についてのべます。
●どんな行列でも零行列との積は零行列となります。
任意の行列Aについて,0A=A0=0
 (この性質は,数の積における0の働きと類似のものです。
(この性質は,数の積における0の働きと類似のものです。
0×a=a×0=0)
●どんな行列も単位行列との積はその行列自身です。
任意の行列Aについて,EA=AE=A

(この性質は,数の積における1の働きと類似のものです。
1×a=a×1=a)
|