← PC用は別頁
|
← PC用は別頁
■これにより  |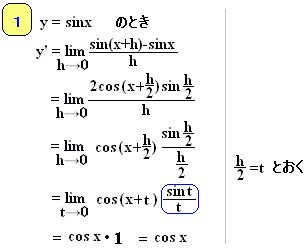
 ※ y=tanxのときはsinx，cosxの結果を用いて商の微分法で求められます。 
（参考）半径１の円（単位円）上の動点P(x,y)を考えると y=sint x=cost 角度がtからdtだけ増えたとき 右図の茶色で示した点から接線に沿って（弧の長さ≒斜辺の長さ）dtの直角三角形を描くと 緑で示した角が平行線の錯角で等しいから，この直角三角形の１つの角はtになる (1) (2) 次に，図のようにtが第１象限の角の場合，tが増えるとxは減少する．そこでdxの符号は負になる． ※この図は，第１象限の場合しか示せていないので，証明としてはやはり上に示した極限値を使った式で行う方がよい． ［まとめ］  |
|
［例題１］
y = sin 3x の導関数を求めなさい。 ［答案例］  ・・答 |
|
［例題２］
 の導関数を求めなさい。
[答案例]  ・・答 |
|
[問題] 次の関数の導関数を求めなさい。
○初めに問題を選び，次に選択肢を選びなさい。正しければ消えます。
○正誤いずれの場合も，解説を読むとができます．解説を読む場合でも読まない場合でも，新たに問題を選べば解答を再開できます． 
|
|
■［個別の頁からの質問に対する回答］[三角関数の導関数について／17.7.2］
拝見していて疑問がありました。
最後の問題の中で、
y=1/(1-tanx)を求める時、
y=1/(1-u)とおいて、
dy/du=1/(1-u)^2とされてるところで、
dy/duは分子が-1ではないでしょうか。
y=1/(1-u)=(1-u)^-1なので。
＝＞［作者］：連絡ありがとう．間違いはないのですが，誤解を招きやすい表現がありましたので（←おい！）詳しく説明しました． |
|
［注］直前にPC版から入られた場合は，自動転送でスマホ版に来ていますので，ブラウザの［戻るキー］では戻れません（堂々巡りになる）．下記のリンクを使ってメニューに戻ってください．
 ...（携帯版）メニューに戻る...（PC版）メニューに戻る |
不定形の極限