← PC�p�͕ʕ�
|
*** ���w�V�i�O�p,�w��,�ΐ�,���������܂ށj ***
 �ς̔��� �ς̔���
 ��,�������̔��� ��,�������̔���
 �������̔��� �������̔���
 �������̔��� �������̔���
 �}��ϐ��\���̂Ƃ��̔����@ �}��ϐ��\���̂Ƃ��̔����@
 ��(2) ��(2)
 �A���̔����@ �A���̔����@
 �d�v�ȋɌ��l(1)_�O�p�� �d�v�ȋɌ��l(1)_�O�p��
 �O�p���̔��� �O�p���̔���
 �w����,�ΐ����̔��� �w����,�ΐ����̔���
 �����i�������K�j �����i�������K�j
 �Q�ߐ��̕����� �Q�ߐ��̕�����
 ��(2) ��(2)
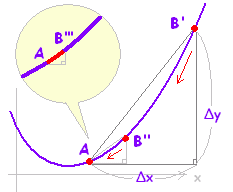
 ���̃O���t�����������.�ɒl.����.�ϋȓ_.�Q�ߐ� ���̃O���t�����������.�ɒl.����.�ϋȓ_.�Q�ߐ�
|