← PC用は別頁
|
*** 数学Ⅲ(三角,指数,対数,無理関数を含む) ***
 積の微分 積の微分
 商,分数関数の微分 商,分数関数の微分
 合成関数の微分 合成関数の微分
 無理関数の微分 無理関数の微分
 媒介変数表示のときの微分法 媒介変数表示のときの微分法
 同(2) 同(2)
 陰関数の微分法 陰関数の微分法
 重要な極限値(1)_三角関数 重要な極限値(1)_三角関数
 三角関数の微分 三角関数の微分
 指数関数,対数関数の微分 指数関数,対数関数の微分
 微分(総合演習) 微分(総合演習)
 漸近線の方程式 漸近線の方程式
 同(2) 同(2)
 関数のグラフ総合・・・増減.極値.凹凸.変曲点.漸近線 関数のグラフ総合・・・増減.極値.凹凸.変曲点.漸近線
|
|
*** 数学Ⅲ(三角,指数,対数,無理関数を含む) ***
 積の微分 積の微分
 商,分数関数の微分 商,分数関数の微分
 合成関数の微分 合成関数の微分
 無理関数の微分 無理関数の微分
 媒介変数表示のときの微分法 媒介変数表示のときの微分法
 同(2) 同(2)
 陰関数の微分法 陰関数の微分法
 重要な極限値(1)_三角関数 重要な極限値(1)_三角関数
 三角関数の微分 三角関数の微分
 指数関数,対数関数の微分 指数関数,対数関数の微分
 微分(総合演習) 微分(総合演習)
 漸近線の方程式 漸近線の方程式
 同(2) 同(2)
 関数のグラフ総合・・・増減.極値.凹凸.変曲点.漸近線 関数のグラフ総合・・・増減.極値.凹凸.変曲点.漸近線
|
|
y' は接線の傾きを表わすので,y' の符号の変化を見れば,増加・減少が分かる. y'>0 のところでは,グラフは増加となる. y'<0 のところでは,グラフは減少となる. 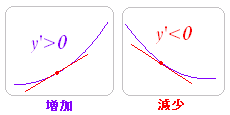 |
|
≪例1≫
y=x2−2x の増減表を求めるには: ■微分して y' を求める ■ y'=2x−2=2(x−1) となる ■ y'=0 となる x の値を求める ■ y'=0 となる x の値は 2(x−1)=0 より x=1 ■ y' の符号を求める ■ x<1 のとき,例えば x=0 のとき y'=−2 だから y' の符号は−になる. x>1 のとき,例えば x=2 のとき y'=2 だから y' の符号は+になる. ■ 増減を矢印で表わす ■ y' の符号が−のときは,y は減少.これを記号 ■ 極値を求める ■ 増加から減少に変化する場所を「極大」といい,そのときの y の値を「極大値」という. 減少から増加に変化する場所を「極小」といい,そのときの y の値を「極小値」という. 極大値と極小値をまとめて極値という. 極値を表に書き込む. この問題では,x=1 のとき,極小値 y=−1 となる. |
||||||||||||||||||||||||
|
以上の結果を表にすると,次のようになる.このような表を増減表という.
x の値は,左に小さな値,右に大きな値があるものとする(数直線と同様)ので,この表の1行目は次のように省略してよい.
|
≪例2≫
y=−2x2+3x の増減表を求めるには: ■微分する ■ y'=x2−4x+3 ■ y'=0 を解く ■ y'=0 ⇔ x2−4x+3=0 ⇔ (x−1)(x−3)=0 ⇔ x=1,3 ■ y' の符号を求める ■ x<1 のとき,例えば x=0 のとき y'=3 だから y' の符号は + 1<x<3 のとき,例えば x=2 のとき y'=−1 だから, y' の符号は− 3<x のとき,例えば x=4 のとき y'=3 だから y' の符号は+ ■ 極値を求める ■ x=1 のとき, y= x=3 のとき, y=0
以上の結果を増減表にすると
|
|
■■ 増減表の作り方(要点) ■■
(1) y' を求める.
上の行は x の値、次の行は y' の符号、一番下の行は y の値を表すものとして,表は上から下へ,左から右へ見ていく.(4) y' の符号は,その区間にある x の一つの値を代入して判断する. (5) y' が+ならば y は増加( |
| (備考) 平成11年告示の高等学校学習指導要領では,数学II で扱う微分は3次関数までとなっていますが,以下の解説においては,数学III や高校卒業後の数学も視野に入れて,この制限を外しています. ■y'=0 が虚数解をもつ場合 次の例1のように,y'=0 が虚数解を持つときは,その虚数解はy' の符号の変わり目とはならないので,y'=0 の実数解から増減表を作ればよい.
≪例1≫
y'=0 の実数解はx=1 ,他の2つの解は虚数y'=(x2+1)(x−1) のとき, このとき,因数 x2+1 の符号はつねに正で,y' の符号に影響していない. したがって,y' の符号は y'=2(x−1) y'=3(x−1) などと全く同じになる. (これらと元の関数を比較すると,y' の値は少し異なるが,符号は全く同じ.増減表においては,y' の値には興味がなく,正,負,0 の符号のみに興味があるから,x2+1 を無視して増減表を作ることができる.) ○ 増減表は次のようになる. y=··· y'=(x2+1)(x−1)
|
||||||||||||||||||||||||||||||||||||
|
■y'=0 が重解,3重解をもつ場合 次の例2のように,y'=0 が(2)重解をもつ点においては,接線の傾きは一度 0 になるが,増減は変化しない. (y' の符号は2回変わる=変化しない)
≪例2≫
y'=0 の実数解はx=1,x=2(重解)y'=(x−1)(x−2)2 のとき となるが, ○ x=2 では y'=0 となるが,x=2 の前後で符号は変化していない. 符号が2回変化すると考えてもよい. (x−2)2 は,2乗だから,つねに ≧0 と考えてもよい. ただし,x=2 では y'=0 となるので,接線の傾きは一度 0 になる. ○ 増減表は次のようになる. y=··· y'=(x−1)(x−2)2
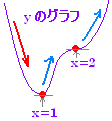 ※ 例2のような場合,y'=0 が重解をもつ点(x=2)は,極値とならない.
y' の符号が, + → 0 → + y' の符号が, - → 0 → - は,崖に道路の図・・・極値でない. 次の例3のように,y'=0 が3重解をもつ点においては,接線の傾きは一度 0 になり,増減は変化する. (y' の符号は3回変わる=1回変る)
≪例3≫
y'=0 の実数解はx=1,x=2(3重解)y'=(x−1)(x−2)3 のとき, となるが, ○ x=2 では y'=0 となって,x=2 の前後で符号は変化する. 符号が3回変化する(1回と同じ)と考えてもよい. ただし,x=2 では y'=0 となるので,接線の傾きは一度 0 になる. ○ 増減表は次のようになる. y=··· y'=(x−1)(x−2)3
 |
|
■問題2 次の各関数について,増減表を完成しなさい. (左から空欄
(1)
y=x4+2x2 y'=4x3+4x=4x(x2+1)
|
||||||||||||||||||
|
|
||||||||||||||||||
|
(2)
y=−(x+1)3 y'=−3(x+1)2
|
||||||||||||||||||
|
(3)
y=3x4−4x3 y'=12x3−12x2=12x2(x−1)
|
||||||||||||||||||
|
|