← PC用は別頁
|
※中学２年生向け「円周角の定理，接弦定理」について，このサイトには次の教材があります． この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください． が現在地です．  ...（携帯版）メニューに戻る...(ＰＣ版)メニューに戻る |
|
※中学２年生向け「円周角の定理，接弦定理」について，このサイトには次の教材があります． この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください． が現在地です． ...（携帯版）メニューに戻る...(ＰＣ版)メニューに戻る |
|
【接弦定理】
【解説】 ≪図で見る証明≫次の図１において
ピンクで示した２つの角度xは等しい
水色で示した２つの角度zは等しい 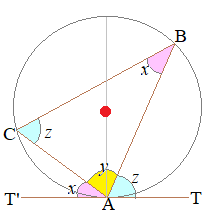 - 図１ - △ABCの内角の和は180°だから右図においてx+y+z=180° また，直線T'AT=180° ※角は３種類ある． ピンクで示した２つのxが等しいこと，水色で示した２つのzが等しいことを示せばよい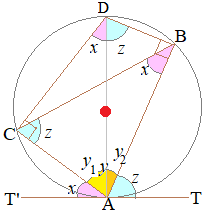．  - 図２ - 円の中心●を通る直径ADを引くと，上２つのピンクのxは弦CAの円周角だから等しい． 次に，直角三角形△DCAにおいてx+y1=90° また，接線と弦CAがなす角xもx+y1=90°を満たす． だから，ピンクで示した３つの角xは等しい． 同様にして，図の水色で示した3つの角zも等しいことが示される． |
|
《問題》
(1) 次の図において，直線ＡＴは点Ａにおける円の接線である．
（以下の欄は，このホームページの作者が個人で追加したものです．）
ＣＡ＝ＣＢ，∠ＡＣＢ＝110  のとき，∠ｘを求めなさい．
（「栃木県 平成11年度」問題の引用）
ＣＡ＝ＣＢだから，∠ＣＢＡ＝∠ＣＡＢとなります．
また，接弦定理により∠ＣＢＡ＝ｘです． △ABCの内角の和は180°だから 2x+110°=180° x=35°…（答） |
|
(2) 次の図のように，三角形ＡＢＣが円Ｏに内接し，直線ＴＴ’は点Ａで円Ｏに接している．
（以下の欄は，このホームページの作者が個人で追加したものです．）
 ，∠ＣＡＴ＝70のとき，∠ＢＡＣの大きさを求めなさい．
（「岐阜県 平成11年度」問題の引用）
 
辺ＡＢ＝ＢＣとなるから，∠ＢＡＣ＝∠ＢＣＡとなります．
また，接弦定理から，∠ＴＡＣ＝∠ＡＢＣです． 2x+70°=180°より x=55°…（答） |
|
(3) 図で，△ＡＢＣは円に内接している．また，Ｄは点Ａにおける円の接線と直線ＣＢとの交点である．∠ＡＣＢ＝35
（以下の欄は，このホームページの作者が個人で追加したものです．）
，∠ＡＤＢ＝45のとき，∠ＢＡＣの大きさは何度か．
（「愛知県Ｂ 平成11年度」問題の引用）
 接弦定理から∠ＤＡＢ＝35°
→∠ＡＢＤ＝100°→∠ＡＢＣ＝80°だから ∠ＢＡＣ＝65°…（答） |
|
...（携帯版）メニューに戻る...（PC版）メニューに戻る
|
| ■このサイト内のGoogle検索■ |