← PC用は別頁
|
※中学２年生向け「円周角の定理，接弦定理」について，このサイトには次の教材があります． この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください． が現在地です．  ...（携帯版）メニューに戻る...(ＰＣ版)メニューに戻る |
|
※中学２年生向け「円周角の定理，接弦定理」について，このサイトには次の教材があります． この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください． が現在地です． ...（携帯版）メニューに戻る...(ＰＣ版)メニューに戻る |
|
《問題》 次の空欄に入る適当な語句を選んで，「接弦定理」の証明を完成させなさい． (証明) 円の接線と弦の作る角が(1)直角(90  )，(2)鋭角(90より小さい)，(3)鈍角(90より大きい)の３つの場合に分けて示すこととします．
(1)
 ＢＡＴ＝90のとき
(漢字２文字を入れなさい↓) 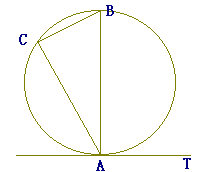ＢＣＡ＝ＢＡＴ＝ＢＣＡが成り立ちます．
 
ABは直径．
したがって，∠BCAは直径の上に立つ円周角で90°． |
|
(2)
ＢＡＴ＜90のとき
( ＢＡＴとＢＣＡを直接比べるのはむずかしいので，ＢＣＡに等しい他の角で比較しました．)
下図のようにＡを通る直径をＡＣ’とすると， (漢字３文字を入れなさい↓) ＢＣＡとＢＣ’Ａは，いずれも(ＢＡＴ内部の)弧ＡＢに対する
だから等しい．
ＢＣＡ＝ＢＣ’Ａ・・・ア
(以下の空欄に数字を入れなさい↓) 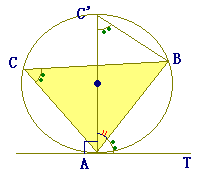ＡＢＣ’＝となり，
ＢＣ’Ａ＋ＢＡＣ’＝ＢＡＴ＋ＢＡＣ’＝ＢＣ’Ａ＝ＢＡＴ・・・イＢＡＴ＝ＢＣＡが成り立ちます．
∠ＢＣＡと∠ＢＣ’Ａは，いずれも
弧ＡＢに対する円周角 ＡＣ’は直径だから∠ＡＢＣ’=90° ∠ＢＣ’Ａ+∠ＢＡＣ’=90° ∠ＢＡＴ+∠ＢＡＣ’=90° |
|
(3)
ＢＡＴ＞90のとき
( ＢＡＴとＢＣＡを直接比べるのはむずかしいので，(2)の結果を利用して．90よりも小さな角で等しいものを探し，下図のようにＣ”とＴ’をとります．)
ＢＡＴ＞90のとき，
ＢＡＴ＋ＢＡＴ’＝・・・アＢＡＴ’＜
(2)の結果から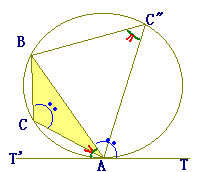， ＢＡＴ’＝ＢＣ”Ａ・・・イＢＡＴ＋ＢＣ”Ａ＝・・・ウＢＣＡ＋ＢＣ”Ａ＝・・・エＢＡＴ＝ＢＣＡが成り立ちます．(証明終り)
∠ＢＡＴ+∠ＢＡＴ’=180°
∠ＢＡＴ’＜90° ∠ＢＡＴ+∠ＢＣ”Ａ=180° ∠ＢＣＡ+∠ＢＣ”Ａ=180° |
≪見た目で覚えたい場合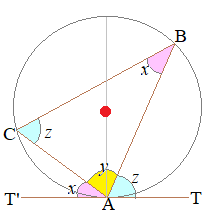1≫
1.△ABCの内角の和は180°だから右図においてx+y+z=180° また，直線T'AT=180° ※角は３種類ある．ピンクで示した２つのxが等しいこと，水色で示した２つのzが等しいことを示せばよい．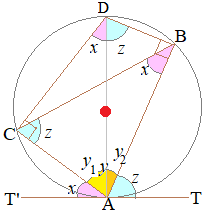 
2.円の中心●を通る直径ADを引くと，上２つのピンクのxは弦CAの円周角だから等しい． 直角三角形△DCAにおいてx+y1=90° 接線と弦CAがなす角xもx+y1=90°を満たす． だから，ピンクで示した３つの角xは等しい． 同様にして，図の水色で示した3つの角zも等しいことが示される． |
≪見た目で覚えたい場合2≫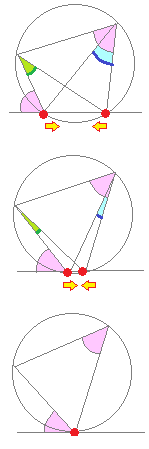
ヒラメさんが目玉を寄せて遊んでいたとする． （右図の●が目玉） (1) 円に内接する四角形では，「１つの内角は向かい合う角の外角に等しい」からピンク色の角は等しい． (2) ２つの目がだんだん寄って来たとき，右図の青と緑で示した角は， だんだん「ちびってきて」 限りなく「０に近付いていく」. (3) ２つの目が完全に重なって１つの目になったとき，「接弦定理」を表す図ができる．
・１つの目を接点とする円の接線が描かれている．
右図でピンク色の角は等しい．・青と緑の角は完全に消える． |
|
［注］直前にPC版から入られた場合は，自動転送でスマホ版に来ていますので，ブラウザの［戻るキー］では戻れません（堂々巡りになる）．下記のリンクを使ってメニューに戻ってください．...（携帯版）メニューに戻る...（PC版）メニューに戻る
|
|
■［個別の頁からの質問に対する回答］[接弦定理 について／17.3.29］
ダッシュが小さくて見辛かったです
＝＞［作者］：連絡ありがとう．Androidなら拡大したら済むことでは？ |
| ■このサイト内のGoogle検索■ |