|
このページのバックアップ・ページ
(グーグルブロガー版)は,こちら⇒ 現在地と前後の項目 集合の要素/集合の表わし方/部分集合,包含関係/共通部分と和集合/補集合/共通部分,和集合,補集合(練習問題)/ド・モルガンの法則/集合(楽しく入門,初歩から)/オイラー図/要素を用いた証明/必要・十分条件(等式)/必要・十分条件(不等式)/必要・十分条件(反例)/必要・十分条件入試問題1/必要・十分条件入試問題2/集合,条件.センター問題(2013~)/p→qの真偽/逆,裏,対偶/対偶証明法と背理法/背理法の入試問題/ 《解説》 ■ 全体集合Uのうち,集合Aを取り除いた残りの部分をAの補集合といい 補集合
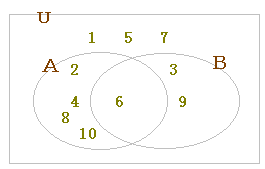
全体集合U={1,2,3,4,5,6,7,8,9},A={1,2,3,5,7}のとき <例2> Uは実数全体の集合,A={x|x>0}のとき, |
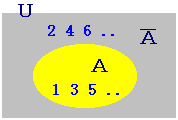

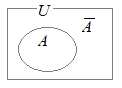
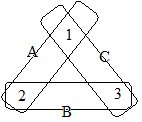 右図の場合,
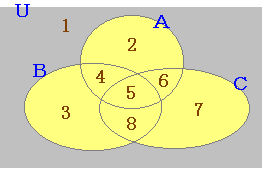
右図の場合,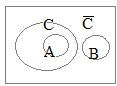 右図のような場合,
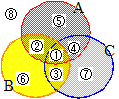
右図のような場合,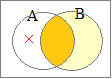 右図において×印の部分がないのだから
右図において×印の部分がないのだから