３項間漸化式の一般項

【 $a_{n+2}=pa_{n+1}+ q a_n$ の形の漸化式】

　定数 $p, q (p\neq 1)$ 係数の３項間漸化式が

$a_{n+2}=p a_{n+ 1}+ q a_n$

の形で与えられているとき，

$a_{n+2}-\alpha a_{n + 1}=\beta (a_{n + 1} - \alpha a_n)$

を満たす定数 $\alpha$ , $\beta$ を見つけると，数列 $a_{n + 1} - \alpha a_n$ は，

初項 $a_2 - \alpha a_1$
公比 $\beta$

の等比数列になるので，
(I)まず２項間漸化式 $a_{n + 1} - \alpha a_n$ の一般項を求めることができます．

１組の定数 $\alpha$ , $\beta$ から得られる２項間漸化式から，さらに数列 $a_n$ の一般項を求めることもできますが，通常の場合，次の（II）の手順で２組の定数 $\alpha$ , $\beta$ から得られる２項間漸化式から連立方程式を解く方が，手順としては簡単になります．

(II)

○上記の $\alpha$ , $\beta$ が「２組求まる場合（２次方程式が異なる実数解を持つ場合）」は，その２組から元の数列の一般項 $a_n$ を求めると簡単になります．
○上記の $\alpha$ , $\beta$ が「１組の解しかない場合（２次方程式が重解を持つ場合）」は，やむを得ず，さらに２項間漸化式を解いて一般項 $a_n$ を求めます．

（解説）

（初歩的な解説）
　３項間漸化式では，前の項 $a_{n+ 1}$ と２つ前の項 $a_n$ を使って $a_{n+ 2}$ が定義されるので，初項だけでなく第２項も具体的な値として与えられていなければ数列を確定することはできません．
　したがって，３項間漸化式の問題では，漸化式以外に初項と第２項の値も使って問題を解きます．

　問題が

$\lbrac$ $a_1=1$ , $a_2=2$
$a_{n+2}=3a_{n+1}-2 a_n$ …(1)

であるとき，

$a_{n+2}-a_{n+1}=2(a_{n+1}-a_n)$ …(2)

または

$a_{n+2}-2a_{n+1}=a_{n+1}-2a_n$ …(3)

のような変形に気付くと，各々数列 $\lbrac a_{n+1}-a_n \rbrac$ , $\lbrac a_{n+1}-2a_n \rbrac$ が等比数列となって，３項間漸化式の問題を２項間漸化式の問題に直すことができます．

(2) →

$\lbrac a_{n+1}-a_n \rbrac$ は公比 $2$ の等比数列になるから
$a_{n+1}-a_n=(a_2-a_1)2^{n-1}=2^{n-1}$ …(2’)

(3) →

$\lbrac a_{n+1}-2 a_n \rbrac$ は公比 $1$ の等比数列になるから
$a_{n+1}-2 a_n=(a_2-2a_1)1^{n-1}=0$ …(3’)

(2’)(3’)を各々２項間漸化式として，さらに，元の数列 $\lbrac a_n \rbrac$ の一般項を求めることもできますが，このように未知数２個 $a_{n+1}$ と $a_n$ に対する連立方程式が得られた場合は，これらの未知数について解くことができます．

この連立方程式は $a_{n+1}$ について解いても $a_n$ についても構いません．･･･ $a_n$ について解けば直接的に $a_n$ の式が得られます． $a_{n+1}$ について解けば（他の普通の連立方程式とは違って） $n$ に $n+1$ を代入した式が得られるので，元に戻す手順が１ステップ必要となります．

○(2’)(3’)を $a_{n+1}$ と $a_n$ に対する連立方程式として解くと
(2’)−(3’)
$a_n=2^{n-1}$ …（答）

もちろん， $a_{n+1}$ についても解けますが，当然の結果が得られ， $a_n$ を求めるために１ステップが余計に必要になります．

(2’)×2−(3’)
$a_{n+1}=2\times 2^{n-1}=2^n$
$a_n=2^{n-1}$ …（答）

○(2’)または(3’)の１つだけを２項間漸化式として解く場合は

(2’)→
$\lbrac a_n \rbrac$ の階差数列 $\lbrac b_n \rbrac$ が与えられていることになるから
$n\geq 2$ のとき
$a_n=a_1+ \sum_{k=1}^{n-1}2^{k-1}=1+\frac{1(2^{n-1}-1)}{2-1}$
$=2^{n-1}$
これは $n=1$ の場合にも成り立つから
$a_n=2^{n-1}$ …（答）

(3’)→から求める場合は
$a_{n+1}=2 a_n$ は公比 $2$ の等比数列であることを示しているから
$a_n=a_1\times 2^{n-1}=2^{n-1}$ …（答）

次の項目→

$\lbrac$ $a_1=1$ , $a_2=2$
$a_{n+2}=3a_{n+1}-2 a_n$ …(1)

のとき，通常，参考書などでは答案の流れは次のようになります．

(1)より特性方程式 $x^2=3x-2$ を解くと
$x=1, 2$ となるから
$\lbrac$ $a_{n+2}-a_{n+1}=2(a_{n+1}-a_n)$ …(1’)
$a_{n+2}-2a_{n+1}=1(a_{n+1}-2a_n)$ …(1”)

※素朴に考えると，「特性方程式」とは何なのか？なぜ特性方程式の解を使えば(1’)(1”)のように変形できるのかという疑問がわきます．･･･速く進もうと「この問題はこうするものだ」と丸暗記してしまうと，実際には特性方程式が使えない場面で使ってしまうミスが起ります．･･･だから，最低でもどの形の問題の場合に特性方程式が使えるのかということは理解しておく必要があります．

▲１　≪特性方程式の解を極限と見る見方≫
　(1)を
$\frac{a_{n+2}}{a_n}=3\frac{a_{n+1}}{a_n}-2$
$\frac{a_{n+2}}{a_{n+1}}\cdot \frac{a_{n+1}}{a_n}=3\frac{a_{n+1}}{a_n}-2$
と変形して，もし，数列 $\frac{a_{n+1}}{a_n}$ に極限値 $\alpha$ が存在したら，すなわち
$\lim_{n\rightarrow \infty}\frac{a_{n+2}}{a_{n+1}}=\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}=\alpha$
ならば， $\alpha$ は
$x^2=3x -2$
で求められることになります．

ただ，この解釈は簡単には納得しにくい話です．
（理由１）

そもそも，なぜ $\frac{a_{n+1}}{a_n}$ の極限なのか，なぜ $a_n$ の

極限を求めないのかが分かりにくい．また，もし極限値がなかったらどうなるのか，極限値が存在することを示されていない

（理由２）

結局のところ
$a_{n+2}\rightarrow x^2$
$a_{n+1}\rightarrow x$
$a_n\rightarrow 1$
と置き換えるということになるが，特になぜ $x^2$ とおくのかがよくわからない

（理由３）

$\lim_{n\rightarrow \infty}\frac{a_{n+2}}{a_{n+1}}=\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}=\alpha$ ， $x^2=3x -2$ と $a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ の間の論理が跳び過ぎていてつながらない

●２　≪ $a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ の形≫から逆算する見方

　(1)を $a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ …(1’)
の形に変形できたらよいのにな～と考えます．

　もし，そのような変形ができなければ以下の方程式が解なしとなるだけだから，試してから判断したらよいと考えます．

　もし，(1’)の形に変形できれば，

第ｎ項が $a_{n+1}-\alpha a_n$
第ｎ+1項が $a_{n+2}-\alpha a_{n+1}$

となる数列 $\lbrac a_{n+1}-\alpha a_n \rbrac$ が公比 $\beta$ の等比数列になって，とりあえず $a_{n+1}-\alpha a_n$ が求まるからです．
　(1’)の $\alpha ,\beta$ は(1)との係数比較により求めることができます．

(1’)→ $a_{n+2}=(\alpha + \beta)a_{n+1}-\alpha \beta a_n$
(1)→ $a_{n+2}=3a_{n+1}-2 a_n$
より $\alpha ,\beta$ は次の連立方程式の解です．
$\lbrac$ $\alpha + \beta=3$ …(2)
$\alpha \beta=2$ …(3)

(2)(3)を素朴に連立方程式として解けば

(2)→ $\beta=3-\alpha$
これを(3)に代入→ $\alpha(3-\alpha)=2$
$\alpha^2-3\alpha + 2=0$ …(4)

(4)より

$(\alpha - 1)(\alpha - 2)=0$
$\alpha=1$ のとき $\beta=2$
$\alpha=2$ のとき $\beta=1$

(2)(3)から $\alpha$ を消去して $\beta$ の方程式にした場合は
$\beta^2-3\beta + 2=0$ …(4’)
になりますが，(4)(4’)を見比べてみると， $\alpha, \beta$ はいずれも，２次方程式
$x^2-3x + 2=0$ …(5)
の解になっているということです．

　通常の解説：
$\lbrac$ $\alpha + \beta=3$ …(2)
$\alpha \beta=2$ …(3)
となる２数は（解と係数の関係により），２次方程式 $x^2-3x + 2=0$
の２つの解だからこれを解きます．
この説明が分かりにくい場合は，上記のように
$\alpha^2-3\alpha + 2=0$ …(4)
$\beta^2-3\beta + 2=0$ …(4’)
はいずれも，２次方程式
$x^2-3x + 2=0$ …(5)
にまとめられると考えればよいでしょう．

次の項目→

【要点】
　 $a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ となる $\alpha , \beta$ を求めたとき
(A)　異なる２つの実数となる場合

$\lbrac$ $a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ …(1)
$a_{n+2}-\beta a_{n+1}=\alpha(a_{n+1}-\beta a_n)$ …(2)

$\lbrac$ $a_{n+1}-\alpha a_n=(a_2-\alpha a_1)\beta^{n-1}$ …(1’)
$a_{n+1}-\beta a_n=(a_2-\beta a_1)\alpha^{n-1}$ …(2’)

(1’)−(2’)により $a_{n+1}$ を消去する

(B)　同じ１つの実数 $\alpha$ となる場合

$a_{n+2}-\alpha a_{n+1}=\alpha(a_{n+1}-\alpha a_n)$

$a_{n+1}-\alpha a_n=(a_2-\alpha a_1)\alpha^{n-1}$

これを２項間漸化式として解く

実際には(A)と全く同様に解けばよい．虚数・無理数・分数係数の数式となるが， $a_1,a_2$ が整数ならばすべての自然数ｎに対して整数値となることは証明できる．
※通常，この形の問題は高校生向けの３項間漸化式の問題としては出題されない．
※複素数のド・モアブルの定理との融合問題としてなら出題されるかもしれない．また，ここで得られる一般項を題材として，虚数・無理数・分数係数の数式がすべての自然数ｎに対して整数値となることの証明問題，計算問題などとして出題されることは考えられる．

【例題１】… $\alpha , \beta$ が異なる２つの実数となる場合
$\lbrac$ $a_1=0$ , $a_2=1$
$a_{n+2}=4a_{n+1}-3 a_n$ …(1)
で定義される数列 $\lbrac a_n \rbrac$ の一般項を求めてください．

（答案１）
　(1)より $a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ …(2)となる $\alpha , \beta$ を求める．
　(2)より $a_{n+2}=(\alpha + \beta)a_{n+1}- \alpha \beta a_n$
これを(1)式と係数比較すると
$\lbrac$ $\alpha + \beta=4$ …(3)
$\alpha \beta=3$ …(4)
この解は
$\alpha=1, \beta=3$ …(5)または $\alpha=3, \beta=1$ …(6)
(5)より

$a_{n+2}- a_{n+1}=3(a_{n+1}-a_n)$
数列 $\lbrac a_{n+1}-a_n \rbrac$ は公比 $3$ の等比数列になるから
$a_{n+1}-a_n=(a_2-a_1)\times 3^{n-1}=3^{n-1}$ …(7)

(6)より

$a_{n+2}- 3 a_{n+1}=a_{n+1}-3 a_n$
数列 $\lbrac a_{n+1}-3 a_n \rbrac$ は公比 $1$ の等比数列になるから
$a_{n+1}-3 a_n=(a_2-3 a_1)\times 1^{n-1}=1$ …(8)

ある数列 $\lbrac b_n \rbrac$ が公比 $1$ の等比数列であれば
$b_1=b_2=b_3=\cdots=b_n$ となり

ある人と友達が同じで，そのまた友達も友達と同じ･･･
⇒全員同じ
（♪友達の友達は友達だ，そのまた友達も友達だ♪⇒定数項になっている数列）

これより直ちに $b_n=b_1$ がいえる．

(7)(8)を未知数 $a_{n+1},a_n$ に関する連立方程式として解く．

$\lbrac$ $x-y$ $=3^{n-1}$
$x-3y$ $=1$
と見て， $x,y$ について解くということです．ただし， $a_n$ を求めるには $y$ だけ求めればよく $x=a_{n+1}$ の方は $n+1$ を代入すれば自動的に得られます．

(7)−(8)
$2a_n=3^{n-1}-1$
$a_n=\frac{3^{n-1}-1}{2}$ …（答）

（答案１’）

　簡単な変形の場合，なぜその変形を思いつくのかという理由を説明しなくても構わない．･･･「目の子算」でも分かるような簡単な移項にまで，くどくどと理由を付ける必要はない．
　だから， $\alpha , \beta$ を別途求めておいて，答案としては次のようにまとめてもよい．

(1)より

$a_{n+2}- a_{n+1}=3(a_{n+1}-a_n)$
数列 $\lbrac a_{n+1}-a_n \rbrac$ は公比 $3$ の等比数列になるから
$a_{n+1}-a_n=(a_2-a_1)\times 3^{n-1}=3^{n-1}$ …(2)

また(1)より

$a_{n+2}- 3 a_{n+1}=a_{n+1}-3 a_n$
数列 $\lbrac a_{n+1}-3 a_n \rbrac$ は公比 $1$ の等比数列になるから
$a_{n+1}-3 a_n=(a_2-3 a_1)\times 1^{n-1}=1$ …(3)

(2)−(3)
$2a_n=3^{n-1}-1$
$a_n=\frac{3^{n-1}-1}{2}$ …（答）

（参考）
この数列において，特性方程式の解 $1,3$ は数列の極限 $\lim_{n\rightarrow \infty}a_n$ を表しているのではなく，隣の項との比の極限 $\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}$ を表しています．
本問のように $a_1\neq a_2$ の場合は $\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}=3$ になり，本問とは異なる初項と第２項で問題が作られていて $a_1=a_2$ となっている場合は $\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}=1$ となることは(2)(3)を少し変形すれば示せます．

次の項目→

【要点】
　 $a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ となる $\alpha , \beta$ を求めたとき
(B)　同じ１つの実数 $\alpha$ となる場合

$a_{n+2}-\alpha a_{n+1}=\alpha(a_{n+1}-\alpha a_n)$

$a_{n+1}-\alpha a_n=(a_2-\alpha a_1)\alpha^{n-1}$

これを２項間漸化式として解く

【例題２】… $\alpha , \beta$ が実数の重解となる場合
$\lbrac$ $a_1=1$ , $a_2=2$
$a_{n+2}=2a_{n+1}- a_n$ …(1)
で定義される数列 $\lbrac a_n \rbrac$ の一般項を求めてください．

(1)より

$a_{n+2}- \alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$
となる $\alpha , \beta$ を求めると
$a_{n+2}=(\alpha + \beta)a_{n+1}-\alpha\beta a_n$ と(1)の係数を比較して
$\lbrac$ $\alpha + \beta=2$
$\alpha \beta=1$
より $\alpha=1 , \beta=1$ の重解となる．

これらの値を代入すると

$a_{n+2}- a_{n+1}=a_{n+1}- a_n$
数列 $\lbrac a_{n+1}- a_n \rbrac$ は公比 $1$ の等比数列（実際には全部等しい数列）になるから
$a_{n+1}- a_n=(a_2- a_1)\times 1^{n-1}=1$ …(2)

(2)より
$a_{n+1}-(n+1)=a_n-n$
数列 $\lbrac a_n- n \rbrac$ は公比 $1$ の等比数列（実際には全部等しい数列）になるから
$a_n-n=a_1-1=0$
$a_n=n$ …（答）

　(2)式以下の変形は，通常は，次のように階差形の漸化式として処理される．
　(2)より数列 $\lbrac a_n \rbrac$ の階差数列を数列 $\lbrac b_n \rbrac$ とすると数列 $b_n=1$ だから
数列 $n\geq 2$ のとき
$a_n=a_1+ \sum_{k=1}^{n-1}1=1+ (n-1)=n$
これは $n=1$ のときも成り立つ
ゆえに， $a_n=n$ …（答）

次の項目→

【要点】
　 $a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ となる $\alpha , \beta$ を求めたとき
(C)　無理数や虚数となる場合

○実際には(A)と全く同様に解けばよい．途中経過が無理数や虚数の数式となり不気味であるが， $a_1,a_2$ が整数ならばすべての自然数ｎに対して $a_n$ が整数値となることは証明できる．
○途中経過が無理数であるにもかかわらず，結果は正の整数となる例として，有名なものにフィボナッチ数列がある．
○ $\alpha , \beta$ が虚数である場合も，(A)と同様に解けばよいが，この形の問題が高校生向けの３項間漸化式の単元で出題されることはめったにない．むしろ，複素数のド・モアブルの定理との融合問題として出題される可能性がある．また，ここで得られる一般項を題材として（数列とか漸化式という言葉を出さずに）途中経過が虚数・無理数となる数式がすべての自然数ｎに対して整数値となることの証明問題，計算問題などとして出題されることは考えられる．

【例題３】… $\alpha , \beta$ が異なる２つの無理数となる場合
$\lbrac$ $a_1=1$
$a_2=1$
$a_{n+2}=a_{n+1}+a_n$ …(1)
で定義される数列 $\lbrac a_n \rbrac$ の一般項を求めてください．
（この数列はフィボナッチ数列と呼ばれる）

この数列を定義に従って順に書き下していくと，

1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , ...

となって，何らあやしいところはない．

（解答）
　(1)より $a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ …(2)となる $\alpha , \beta$ を求める．
　(2)より $a_{n+2}=(\alpha + \beta)a_{n+1}- \alpha \beta a_n$
これを(1)式と係数比較すると
$\lbrac$ $\alpha + \beta=1$ …(3)
$\alpha \beta=-1$ …(4)
この解は
$\frac{1-\sqrt{5}}{2}, \frac{1+\sqrt{5}}{2}$
の２数

$a_{n+2}- \alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$
数列 $\lbrac a_{n+1}-\alpha a_n \rbrac$ は公比 $\beta$ の等比数列になるから
$a_{n+1}-\alpha a_n=(a_2-\alpha a_1)\times \beta^{n-1}=(1-\alpha)\beta^{n-1}$
ここで(3)より $1-\alpha=\beta$ であるから
$a_{n+1}-\alpha a_n=\beta^n$ …(5)

同様にして
$a_{n+2}- \beta a_{n+1}=\alpha(a_{n+1}-\beta a_n)$ より
$a_{n+1}-\beta a_n=\alpha^n$ …(6)
(5)−(6)
$(\beta-\alpha) a_n=\beta^n-\alpha^n$
$a_n=\frac{\beta^n-\alpha^n}{\beta-\alpha}=\frac{ \left(\frac{1+ \sqrt{5}}{2}\right)^n- \left(\frac{1- \sqrt{5}}{2}\right)^n}{\sqrt{5}}$ …（答）

※最終結果の式が無理数・分数になっており，本当にこれで正しのか不気味な印象を受ける．そこで，各項を調べてみると
■ $n=1$ → $a_1=\frac{ \left(\frac{1+ \sqrt{5}}{2}\right)- \left(\frac{1- \sqrt{5}}{2}\right)}{\sqrt{5}}=1$ ：整数
$n=2$ → $a_2=\frac{ \left(\frac{1+ \sqrt{5}}{2}\right)^2- \left(\frac{1- \sqrt{5}}{2}\right)}{\sqrt{5}}^2=1$ ：整数

$a_n=\frac{\beta^n-\alpha^n}{\beta-\alpha}, a_{n+1}=\frac{\beta^{n+1}-\alpha^{n+1}}{\beta-\alpha}$ が整数であるならば
$a_{n+2}=\frac{\beta^{n+2}-\alpha^{n+2}}{\beta-\alpha}$
$=\frac{(\beta^{n+1}-\alpha^{n+1})(\beta+\alpha)+\alpha^{n+1}\beta-\alpha\beta^{n+1}}{\beta-\alpha}$
$=\frac{(\beta^{n+1}-\alpha^{n+1})(\beta+\alpha)}{\beta-\alpha}-\frac{\alpha\beta(\beta^n-\alpha^n)}{\beta-\alpha}$
$\alpha + \beta=1, \alpha\beta=1$ だから
$a_{n+2}=\frac{\beta^{n+1}-\alpha^{n+1}}{\beta-\alpha}-\frac{\beta^n-\alpha^n}{\beta-\alpha}$
は整数−整数で整数になる．■

(1)式で定義されることを考えると，前の２項が整数であるならば次の項も整数であることは当然であるが，数列・漸化式という枠組みを隠して，次の形で出題されることが多い．
「すべての自然数ｎについて
$\frac{ \left(\frac{1+ \sqrt{5}}{2}\right)^n- \left(\frac{1- \sqrt{5}}{2}\right)^n}{\sqrt{5}}$
は整数になることを証明せよ．」
これに対しては上記の■～■のように答えるとよい．

【例題４】… $\alpha , \beta$ が２つの共役複素数となる場合
$\lbrac$ $a_1=0$
$a_2=1$
$a_{n+2}=a_{n+1}-a_n$ …(1)
で定義される数列 $\lbrac a_n \rbrac$ の一般項を求めてください．

この数列を定義に従って順に書き下していくと，

0 , 1 , 1 , 0 , −1 , −1 , 0 , 1 , 1 , ...

となって，６個周期で同じ値となる．

（解答）
　(1)より $a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ …(2)となる $\alpha , \beta$ を求める．
　(2)より $a_{n+2}=(\alpha + \beta)a_{n+1}- \alpha \beta a_n$
これを(1)式と係数比較すると
$\lbrac$ $\alpha + \beta=1$ …(3)
$\alpha \beta=1$ …(4)
この解は
$\frac{1-\sqrt{3}i}{2}, \frac{1+\sqrt{3}i}{2}$
の２数

同様にして
$a_{n+2}- \beta a_{n+1}=\alpha(a_{n+1}-\beta a_n)$ より
$a_{n+1}-\beta a_n=(a_2-\beta a_1)\alpha^{n-1}=\alpha^{n-1}$ …(6)
(5)−(6)
$(\beta-\alpha) a_n=\beta^{n-1}-\alpha^{n-1}$
$a_n=\frac{\beta^{n-1}-\alpha^{n-1}}{\beta-\alpha}=\frac{ \left(\frac{1+ \sqrt{3}i}{2}\right)^{n-1}- \left(\frac{1- \sqrt{3}i}{2}\right)^{n-1}}{\sqrt{3}i}$ …（答）

※この一般項も虚数のｎ乗で表されており，すべての自然数ｎについて $a_n$ が整数になるのは奇妙に思えるが･･･

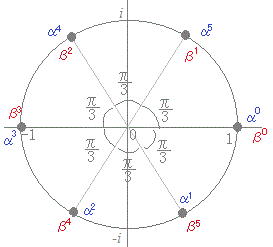
複素数平面上で $\alpha=\frac{1-\sqrt{3}i}{2}, \beta=\frac{1+\sqrt{3}i}{2}$ は図のような単位円を６等分する点にある．複素数については，ド・モアブルの定理により
$(\cos\alpha+ i \sin\alpha)^n=\cos n\alpha + i \sin n\alpha$
$(\cos\beta+ i \sin\beta)^n=\cos n\beta + i \sin n\beta$
が成り立つから，各々図のような位置にある．
　差を取ると実部が消えて，虚部の２倍が残るから， $\beta^{n-1}-\alpha^{n-1}$ の取る値は
$0,\sqrt{3}i,\sqrt{3}i,0,-\sqrt{3}i,-\sqrt{3}i,...$
の６個の値を順に繰り返し， $\beta-\alpha=\sqrt{3}i$ だから
$a_n=\frac{\beta^n-\alpha^n}{\beta-\alpha}$ は $0,1,1,0,-1,-1,...$ の値を順に繰り返す．

【⇒とにかく答を出すには】

　以下を用いれば，異なる２つの解をもつときは，例題３，例題４のような問題のどちらでも解けます．
　通常，答案を書くときに教科書や参考書に広く書かれている事柄は省略してもよいと解釈されていまが，以下の解き方：特に $a_n=A\alpha^{n-1}+ B \beta^{n-1}$ とおけるということは広く書かれているとは言えないので，上記の解答のように係数比較から導くなどの根拠も書かないと少しは減点されるかもしれない．
　この項目は「とにかく答を出すには」「検算するには」･･･という話

$\lbrac$ $a_1$
$a_2$
$a_{n+2}+ p a_{n+1}+ q a_n=0$ …(1)

$a_n=A\alpha^{n-1}+ B \beta^{n-1}$
となる $A,B$ を求めるとよい．

（解説）
$a_{n+2}+ p a_{n+1}+ q a_n=0$ …(1)を
$a_{n+2}-\alpha a_{n+1}=\beta (a_{n+1} -\alpha a_n)$ …(2)
$a_{n+2}-\beta a_{n+1}=\alpha (a_{n+1} -\beta a_n)$ …(3)
とおいたとき， $\alpha\neq \beta$ であれば
(2) → $a_{n+1} -\alpha a_n=(a_2 - \alpha a_1)\beta^{n-1}$ …(2’)
(3) → $a_{n+1} -\beta a_n=(a_2 - \beta a_1)\alpha^{n-1}$ …(3’)
(2’)−(3’)
$(\beta-\alpha) a_n=-(a_2 - \beta a_1)\alpha^{n-1}+(a_2 - \alpha a_1)\beta^{n-1}$
$a_n=\frac{-(a_2 - \beta a_1)\alpha^{n-1}+(a_2 - \alpha a_1)\beta^{n-1}}{\beta-\alpha}$
$=A\alpha^{n-1}+ \beta^{n-1}$
と書ける．ここで $\alpha,\beta$ が固定されているとき， $A,B$ は $a_1,a_2$ で定まる定数．
そこで， $a_1,a_2$ の値を代入して $A,B$ を求めたら答が得られる．

【例題３】（再掲）
$\lbrac$ $a_1=1$
$a_2=1$
$a_{n+2}=a_{n+1}+a_n$ …(1)

（解答）
(1)の特性方程式 $x^2-x-1=0$ の解は $\alpha=\frac{1-\sqrt{5}}{2},\beta=\frac{1+\sqrt{5}}{2}$
一般項を
$a_n=A\alpha^{n-1}+ \beta^{n-1}$
とおくと
$a_1=1$ より $A+ B=1$
$a_2=1$ より $A\alpha+ B\beta=1$
これを $A,B$ について解くと
$A=\frac{1-\beta}{\alpha-\beta},B=\frac{1-\alpha}{\beta-\alpha}$
ここで $\alpha-\beta=-\sqrt{5},\beta-\alpha=\sqrt{5},1-\alpha=\beta,1-\beta=\alpha$ だから
$a_n=\frac{\alpha^n}{-\sqrt{5}}+\frac{\beta^n}{\sqrt{5}}=\frac{\beta^n-\alpha^n}{\sqrt{5}}$
$=\frac{ \left(\frac{1+ \sqrt{5}}{2}\right)^n- \left(\frac{1- \sqrt{5}}{2}\right)^n}{\sqrt{5}}$ …（答）

【例題4】（再掲）
$\lbrac$ $a_1=0$
$a_2=1$
$a_{n+2}=a_{n+1}-a_n$ …(1)

（解答）
(1)の特性方程式 $x^2-x+1=0$ の解は $\alpha=\frac{1-\sqrt{3}i}{2},\beta=\frac{1+\sqrt{3}i}{2}$
一般項を
$a_n=A\alpha^{n-1}+ \beta^{n-1}$
とおくと
$a_1=0$ より $A+ B=0$
$a_2=1$ より $A\alpha+ B\beta=1$
これを $A,B$ について解くと
$A=\frac{1}{\alpha-\beta}=\frac{1}{-\sqrt{3}i},B=\frac{1}{\beta-\alpha}=\frac{1}{\sqrt{3}i}$
だから
$a_n=\frac{\alpha^{n-1}}{-\sqrt{3}i}+\frac{\beta^{n-1}}{\sqrt{3}i}=\frac{\beta^{n-1}-\alpha^{n-1}}{\sqrt{3}i}$
$=\frac{ \left(\frac{1+ \sqrt{3}i}{2}\right)^{n-1}- \left(\frac{1- \sqrt{3}i}{2}\right)^{n-1}}{\sqrt{3}i}$ …（答）

次の項目→

(1)～(4)は $\alpha, \beta$ が２組定まる問題

(1)	$a_1=1$ $a_2=2$ $a_{n+2}=3a_{n+1}-2a_n$	$a_n=2^{n-1}$	[？]
(2)	$a_1=0$ $a_2=1$ $a_{n+2}=5a_{n+1}-6a_n$	$a_n=3^{n-1}-2^{n-1}$	[？]
(3)	$a_1=0$ $a_2=1$ $a_{n+2}-a_{n+1}-2a_n=0$	$a_n=\frac{2^{n-1}-(-1)^{n-1}}{3}$	[？]
(4)	$a_1=1$ $a_2=2$ $a_{n+2}=\frac{a_{n+1}+a_n}{2}$	$a_n=\frac{2}{3}\left( \frac{5}{2}-(-\frac{1}{2})^{n-1}\right)$	[？]

(5)～(7)は $\alpha, \beta$ が１組だけ定まる問題

(5)	$a_1=0$ $a_2=2$ $a_{n+2}=4a_{n+1}-4a_n$	$a_n=(n-1)2^{n-1}$	[？]
(6)	$a_1=1$ $a_2=2$ $a_{n+2}=6a_{n+1}-9a_n$	$a_n=(4-n)3^{n-2}$	[？]
(7)	$a_1=0$ $a_2=1$ $a_{n+2}=\frac{4a_{n+1}-a_n}{4}$	$a_n=\frac{n-1}{2^{n-2}}$	[？]

(8)～(11)は $\alpha, \beta$ が異なる２つの無理数または虚数になる問題
※やや難しい：基本問題とは言えない！

(8)	$a_1=0$ $a_2=1$ $a_{n+2}=2a_{n+1}+ a_n$	$a_n=\frac{(1+\sqrt{2})^{n-1}-(1-\sqrt{2})^{n-1}}{2\sqrt{2}}$	[？]
(9)	$a_1=1$ $a_2=2$ $a_{n+2}=\frac{2a_{n+1}+ a_n}{2}$	$a_n=\left(\frac{1-\sqrt{3}}{2} \right)^n+\left(\frac{1+\sqrt{3}}{2} \right)^n$	[？]
(10)	$a_1=0$ $a_2=1$ $a_{n+2}=2a_{n+1}-2 a_n$	$a_n=\frac{(1+i)^{n-1}-(1-i)^{n-1}}{2i}$	[？]
(11)	$a_1=0$ $a_2=1$ $a_{n+2}+ a_{n+1} + a_n=0$	$a_n=\frac{\left(\frac{-1+\sqrt{3}i}{2}\right)^{n-1}-\left(\frac{-1-\sqrt{3}i}{2}\right)^{n-1}}{\sqrt{3}i}$	[？]

次の項目→

【問題】 …（簡単な再現問題です）
　次の漸化式で定義される数列の一般項を求めてください．（** HELPが必要なときは，上記の例題などを見てください **）
　はじめに左欄の定義式を選び，続いて右欄の一般項を選んでください．やり直すときは，右欄を連打するのでなく，左欄の問題を選び直すことから始めてください．

(1)

$a_1=1$
$a_2=2$
$a_{n+2}=3a_{n+1}-2a_n$

(2)

$a_1=1$
$a_2=2$
$a_{n+2}=\frac{a_{n+1}+ a_n}{2}$

(3)

$a_1=1$
$a_2=2$
$a_{n+2}=2 a_{n+1}-a_n$

(4)

$a_1=0$
$a_2=2$
$a_{n+2}=4a_{n+1}-4a_n$

(5)

$a_1=1$
$a_2=1$
$a_{n+2}=a_{n+1}+ a_n$

$a_n=n$

$a_n=n!$

$a_n=2^{n-1}$

$a_n=(n-1)2^{n-1}$

$a_n=\frac{2}{3} \lbrac \frac{5}{2}-\left(-\frac{1}{2}\right)^{n-1} \rbrac$

$a_n=\frac{\left(\frac{1+\sqrt{5}}{2} \right)^n-\left(\frac{1-\sqrt{5}}{2} \right)^n}{\sqrt{5}}$
*** END ***

$a_1=1$
$a_2=2$
$a_{n+2}=3a_{n+1}-2a_n$ …(1)

$a_{n+2}- a_{n+1}=2(a_{n+1}-a_n)$ …(2)
$a_{n+2}- 2 a_{n+1}=a_{n+1}-2 a_n$ …(3)
(2)より数列 $\lbrac a_{n+1}-a_n \rbrac$ は公比 $2$ の等比数列になるから
$a_{n+1}-a_n=(a_2-a_1)\times 2^{n-1}=2^{n-1}$ …(2’)
(3)より数列 $\lbrac a_{n+1}-2a_n \rbrac$ は公比 $1$ の等比数列になるから
$a_{n+1}-2 a_n=(a_2-2 a_1)\times 1^{n-1}=0$ …(3’)
(2’)−(3’)
$a_n=2^{n-1}$ …（答）

（参考）
この数列において，特性方程式の解 $1,2$ は数列の極限 $\lim_{n\rightarrow \infty}a_n$ を表しているのではなく，隣の項との比の極限 $\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}$ を表しています．
本問のように $a_1\neq a_2$ の場合は $\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}=2$ になり，本問とは異なる初項と第２項で問題が作られていて $a_1=a_2$ となっている場合は $\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}=1$ となることは(2’)(3’)を少し変形すれば示せます．（以下の問題についても同様です）

［←戻る］

$a_1=0$
$a_2=1$
$a_{n+2}=5a_{n+1}-6a_n$ …(1)

$a_{n+2}- 2a_{n+1}=3(a_{n+1}-2a_n)$ …(2)
$a_{n+2}- 3a_{n+1}=2(a_{n+1}-3 a_n)$ …(3)
(2)より数列 $\lbrac a_{n+1}-2a_n \rbrac$ は公比 $3$ の等比数列になるから
$a_{n+1}-2a_n=(a_2-2a_1)\times 3^{n-1}=3^{n-1}$ …(2’)
(3)より数列 $\lbrac a_{n+1}-3a_n \rbrac$ は公比 $2$ の等比数列になるから
$a_{n+1}-3 a_n=(a_2-3 a_1)\times 2^{n-1}=2^{n-1}$ …(3’)
(2’)−(3’)
$a_n=3^{n-1}-2^{n-1}$ …（答）
［←戻る］

$a_1=0$
$a_2=1$
$a_{n+2}-a_{n+1}-2a_n=0$ …(1)

$a_{n+2}+a_{n+1}=2(a_{n+1}+a_n)$ …(2)
$a_{n+2}- 2a_{n+1}=(-1)(a_{n+1}-2 a_n)$ …(3)
(2)より数列 $\lbrac a_{n+1}+a_n \rbrac$ は公比 $2$ の等比数列になるから
$a_{n+1}+a_n=(a_2+a_1)\times 2^{n-1}=2^{n-1}$ …(2’)
(3)より数列 $\lbrac a_{n+1}-2a_n \rbrac$ は公比 $-1$ の等比数列になるから
$a_{n+1}-2 a_n=(a_2-2 a_1)\times (-1)^{n-1}=(-1)^{n-1}$ …(3’)
(2’)−(3’)
$3a_n=2^{n-1}-(-1)^{n-1}$
$a_n=\frac{2^{n-1}-(-1)^{n-1}}{3}$ …（答）
［←戻る］

$a_1=1$
$a_2=2$
$a_{n+2}=\frac{a_{n+1}+a_n}{2}$ …(1)

$a_{n+2}-a_{n+1}=\left(-\frac{1}{2}\right)(a_{n+1}-a_n)$ …(2)
$a_{n+2}+\frac{1}{2}a_{n+1}=a_{n+1}+\frac{1}{2} a_n$ …(3)
(2)より数列 $\lbrac a_{n+1}-a_n \rbrac$ は公比 $-\frac{1}{2}$ の等比数列になるから
$a_{n+1}-a_n=(a_2-a_1)\times \left(-\frac{1}{2}\right)^{n-1}=\left(-\frac{1}{2}\right)^{n-1}$ …(2’)
(3)より数列 $\lbrac a_{n+1}+ \frac{1}{2}a_n \rbrac$ は公比 $1$ の等比数列（すべての項が等しい数列）になるから
$a_{n+1}+ \frac{1}{2} a_n=(a_2+ \frac{1}{2} a_1)\times 1^{n-1}=\frac{5}{2}$ …(3’)
(2’)−(3’)
$-\frac{3}{2}a_n=\left(-\frac{1}{2}\right)^{n-1}-\frac{5}{2}$
$a_n=\frac{2}{3}\lbrac\frac{5}{2}-\left(-\frac{1}{2} \right)^{n-1} \rbrac$ …（答）
［←戻る］

$a_1=0$
$a_2=2$
$a_{n+2}=4a_{n+1}-4a_n$ …(1)

$a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ となる $\alpha, \beta$ を求める．
$a_{n+2}=(\alpha + \beta)a_{n+1}-\alpha\beta a_n$ と(1)を係数比較すると

$\alpha + \beta=4$
$\alpha \beta=4$
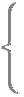
より $\alpha=2,\beta=2$ （２次方程式では重解の場合）
$a_{n+2}-2a_{n+1}=2(a_{n+1}-2a_n)$ …(2)
(2)より数列 $\lbrac a_{n+1}-2a_n \rbrac$ は公比 $2$ の等比数列になるから
$a_{n+1}-2a_n=(a_2-2a_1)\times 2^{n-1}=2^n$
$a_{n+1}=2a_n+ 2^n$ …(2’)
(2’)を２項間漸化式として解く
$a_{n+1}-(n+1)\times 2^n=2(a_n-n\times 2^{n-1})$ …(*)
数列 $\lbrac a_n - n\times 2^{n-1}\rbrac$ は公比 $2$ の等比数列になるから
$a_n-n\times 2^{n-1}=(a_1-1\times 2^0)2^{n-1}=-2^{n-1}$
$a_n=n\times 2^{n-1}-2^{n-1}=(n-1)2^{n-1}$ …（答）

（参考）
(2’)のように $a_{n+1}=pa_n+ q^n$ の形をしている漸化式は，通常は
$a_{n+1}-\alpha q^{n+1}=p(a_n-\alpha q^n)$ と変形できるが，この問題のように $p=q$ となっている場合は $\alpha$ が定まらない．このような場合には，
$a_{n+1}-\alpha(n+1) q^{n+1}=p(a_n-\alpha n q^n)$
とおけばよい．これにより，本問では
$a_{n+1}-\alpha(n+1) 2^{n+1}=2(a_n-\alpha n 2^n)$
より
$\alpha(n+1) 2^{n+1}-2\alpha n 2^n\alpha 2^{n+1}=2^n$
から
$\alpha=\frac{1}{2}$ が求まる．

普通，参考書では(2’)以下の答案は，次のように書かれるが，かなり長い答案になる：

(2’)の両辺を $2^{n+1}$ で割る．
$\frac{a_{n+1}}{2^{n+1}}=\frac{a_n}{2^n}+ \frac{1}{2}$
$\frac{a_n}{2^n}=b_n$ とおくと（この $b_n$ は階差数列ではなく置き換えた式の名前）
$b_{n+1}=b_n+ \frac{1}{2}$
$b_n$ の階差数列を $c_n$ とおくと
$c_n=\frac{1}{2}$
$n \geq 2$ のとき
$b_n=b_1+\sum_{k=1}^{n-1}\frac{1}{2}=0+ \frac{n-1}{2}=\frac{n-1}{2}$
$n=1$ のときも結果が一致するから
$b_n=\frac{n-1}{2}$
したがって
$\frac{a_n}{2^n}=\frac{n-1}{2}$
$a_n=(n-1)2^{n-1}$ …（答）

［←戻る］

$a_1=1$
$a_2=2$
$a_{n+2}=6a_{n+1}-9a_n$ …(1)

$a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ となる $\alpha, \beta$ を求める．
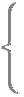
$a_{n+2}=(\alpha + \beta)a_{n+1}-\alpha\beta a_n$ と(1)を係数比較すると

$\alpha + \beta=6$
$\alpha \beta=9$
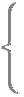
より $\alpha=3,\beta=3$ （２次方程式では重解の場合）
$a_{n+2}-3a_{n+1}=3(a_{n+1}-3a_n)$ …(2)
(2)より数列 $\lbrac a_{n+1}-3a_n \rbrac$ は公比 $3$ の等比数列になるから
$a_{n+1}-3a_n=(a_2-3a_1)\times 3^{n-1}=3^{n-1}$
$a_{n+1}=3a_n-3^{n-1}$ …(2’)
(2’)を２項間漸化式として解く
$a_{n+1}-\alpha(n+1)\times 3^{n+1}=3(a_n-\alpha n\times 3^n)$ …(*)
(*)と(2’)を係数比較すると
$\alpha \times 3^{n+1}=3^{n-1}$
$\alpha =-\frac{1}{9}$
ゆえに
$a_{n+1}+(n+1)3^{n-1}=3(a_n+ n 3^{n-2})$
数列 $\lbrac a_n + n\times 3^{n-2}\rbrac$ は公比 $3$ の等比数列になるから
$a_n+ n\times 3^{n-2}=(a_1+ 1\times 3^{-1})3^{n-1}=\frac{4}{3}\times 3^{n-1}$
$a_n=\frac{4}{3}\times 3^{n-1}- n\times 3^{n-2}$
$a_n=(4-n)3^{n-2}$ …（答）

普通，参考書では(2’)以下の答案は，次のように書かれるが，かなり長い答案になる：

(2’)の両辺を $3^{n+1}$ で割る．
$\frac{a_{n+1}}{3^{n+1}}=\frac{a_n}{3^n}- \frac{1}{9}$
$\frac{a_n}{3^n}=b_n$ とおくと（この $b_n$ は階差数列ではなく置き換えた式の名前）
$b_{n+1}=b_n- \frac{1}{9}$
$b_n$ の階差数列を $c_n$ とおくと
$c_n=-\frac{1}{9}$
$n \geq 2$ のとき
$b_n=b_1+\sum_{k=1}^{n-1}\left(-\frac{1}{9}\right)=\frac{a_1}{3}+ \left(\frac{1}{9}\right)(n-1)$
$=\frac{1}{3}-\frac{n}{9}+\frac{1}{9}=\frac{4-n}{9}$
$n=1$ のときも結果が一致するから
$b_n=\frac{4-n}{9}$
したがって
$\frac{a_n}{3^n}=\frac{4-n}{9}$
$a_n=\frac{4-n}{9}\times 3^n=(4-n)3^{n-2}$ …（答）

［←戻る］

$a_1=0$
$a_2=1$
$a_{n+2}=\frac{4a_{n+1}-a_n}{4}$ …(1)

$a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$ となる $\alpha, \beta$ を求める．
$a_{n+2}=(\alpha + \beta)a_{n+1}-\alpha\beta a_n$ と(1)を係数比較すると

$\alpha + \beta=1$
$\alpha \beta=\frac{1}{4}$
より $\alpha=\beta=\frac{1}{2}$ （２次方程式では重解の場合）
$a_{n+2}-\frac{1}{2}a_{n+1}=\frac{1}{2}(a_{n+1}-\frac{1}{2}a_n)$ …(2)
(2)より数列 $\lbrac a_{n+1}-\frac{1}{2}a_n \rbrac$ は公比 $\frac{1}{2}$ の等比数列になるから
$a_{n+1}-\frac{1}{2}a_n=(a_2-\frac{1}{2}a_1)\times \left(\frac{1}{2}\right)^{n-1}=\left(\frac{1}{2}\right)^{n-1}$
$a_{n+1}=\frac{1}{2}a_n+\frac{1}{2^{n-1}}$ …(2’)
(2’)を２項間漸化式として解く
$a_{n+1}-\alpha \frac{n+1}{2^{n+1}}=\frac{1}{2}(a_n-\alpha \frac{n}{2^n})$ …(*)
(*)と(2’)を係数比較すると
$\alpha \frac{n+1}{2^{n+1}}-\alpha \frac{n}{2^{n+1 }}=\frac{\alpha}{2^{n+1}}=\frac{1}{2^{n-1}}$
$\alpha =\frac{1}{4}$
ゆえに
$a_{n+1}-\frac{n+1}{2^{n-1}}=\frac{1}{2}(a_n-\frac{n}{2^{n-2}})$
数列 $\lbrac a_n - \frac{n}{2^{n-2}}\rbrac$ は公比 $\frac{1}{2}$ の等比数列になるから
$a_n- \frac{n}{2^{n-2}}=(a_1-\frac{1}{2^{-1}})\left(\frac{1}{2}\right)^{n-1}=-2\times \frac{1}{2^{n-1}}$
$=-\frac{1}{2^{n-2}}$
$a_n=\frac{n}{2^{n-2}}-\frac{1}{2^{n-2}}=\frac{n-1}{2^{n-2}}$ …（答）
［←戻る］

$a_1=0$
$a_2=1$
$a_{n+2}=2a_{n+1}+a_n$ …(1)

(1)の特性方程式 $x^2-2x-1=0$ の解は $\alpha=1-\sqrt{2},\beta=1+\sqrt{2}$
一般項を
$a_n=A\alpha^{n-1}+ \beta^{n-1}$
とおくと
$a_1=0$ より $A+ B=0$
$a_2=1$ より $A\alpha+ B\beta=1$
これを $A,B$ について解くと
$A=\frac{1}{\alpha-\beta}=\frac{1}{-2\sqrt{2}},B=\frac{1}{\beta-\alpha}=\frac{1}{2\sqrt{2}}$
だから
$a_n=\frac{(1+\sqrt{2})^{n-1}-(1-\sqrt{2})^{n-1} }{2\sqrt{2}}$ …（答）
［←戻る］

$a_1=1$
$a_2=2$
$a_{n+2}=\frac{2a_{n+1}+a_n}{2}$ …(1)

(1)の特性方程式 $2x^2-2x-1=0$ の解は $\alpha=\frac{1-\sqrt{3}}{2},\beta=\frac{1+\sqrt{3}}{2}$
一般項を
$a_n=A\alpha^{n-1}+ \beta^{n-1}$
とおくと
$a_1=1$ より $A+ B=1$
$a_2=2$ より $A\alpha+ B\beta=2$
これを $A,B$ について解くと
$A=\frac{2-\beta}{\alpha-\beta}=-\sqrt{3}\alpha,B=\frac{2-\alpha1}{\beta-\alpha}=\sqrt{3}\beta$
だから
$a_n=\left(\frac{1-\sqrt{3}}{2}\right)^n+\left(\frac{1+\sqrt{3}}{2}\right)^n$ …（答）
［←戻る］

$a_1=0$
$a_2=1$
$a_{n+2}=2a_{n+1}-2a_n$ …(1)

(1)の特性方程式 $x^2-2x+2=0$ の解は $\alpha=1-i,\beta=1+1$
一般項を
$a_n=A\alpha^{n-1}+ \beta^{n-1}$
とおくと
$a_1=0$ より $A+ B=0$
$a_2=1$ より $A\alpha+ B\beta=1$
これを $A,B$ について解くと
$A=\frac{1}{\alpha-\beta}=-\frac{1}{2i},B=\frac{1}{\beta-\alpha}=\frac{1}{2i}$
だから
$a_n=\frac{(1-i)^{n-1}}{-2i}+\frac{(1+i)^{n-1}}{2i}=\frac{(1+ i)^{n-1}-(1-i)^{n-1}}{2i}$ …（答）
［←戻る］

$a_1=0$
$a_2=1$
$a_{n+2}+ a_{n+1} + a_n=0$ …(1)

(1)の特性方程式 $x^2+ x+1=0$ の解は $\alpha=\frac{-1-\sqrt{3}i}{2},\beta=\frac{-1+\sqrt{3}i}{2}$
一般項を
$a_n=A\alpha^{n-1}+ \beta^{n-1}$
とおくと
$a_1=0$ より $A+ B=0$
$a_2=1$ より $A\alpha+ B\beta=1$
これを $A,B$ について解くと
$A=\frac{1}{\alpha-\beta}=-\frac{1}{\sqrt{3}i},B=\frac{1}{\beta-\alpha}=\frac{1}{\sqrt{3}i}$
だから
$a_n=\frac{\alpha^{n-1}}{-\sqrt{3}i}+\frac{\beta^{n-1}}{\sqrt{3}i}$
$=\frac{\left(\frac{-1+\sqrt{3}i}{2}\right)^{n-1}-\left(\frac{-1-\sqrt{3}i}{2}\right)^{n-1}}{\sqrt{3}i}$ …（答）
［←戻る］