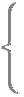漸化式と一般項（等比形）

【 $a_{n+1}=pa_n+q$ の形の漸化式】

　定数 $p, q (p\neq 1)$ 係数の２項間漸化式が

$a_{n+1}=pa_n+q$

の形で与えられているとき，

$a_{n+1}-\alpha =p(a_n - \alpha)$

を満たす定数 $\alpha$ を見つけると，数列 $a_n - \alpha$ は，

初項 $a_1 - \alpha$
公比 $p$

の等比数列になるので，一般項を求めることができます．

（解説）
　もし問題が

$\lbrac$ $a_1=1$
$a_{n+1}=3a_n$ …(1)

の形であるならば，この数列 $\lbrac a_n \rbrac$ は，初項 $1$ 公比 $3$ の等比数列だから，直ちに一般項が求まります．

$a_n=a_1\times r^{n-1}=3^{n-1}$

　これに対して，問題が

$\lbrac$ $a_1=1$
$a_{n+1}=3a_n$ $+2$ …(2)

のような形になっているとき，このままの形では数列 $\lbrac a_n \rbrac$ は，等比数列にはなりませんが，

$a_{n+1}+1=3(a_n+1)$ …(2’)

と変形すると，数列 $\lbrac a_n + 1\rbrac$ は等比数列になるので

$a_n+ 1=(a_1+1)\times 3^{n-1}=2\times 3^{n-1}$
$a_n=2\times 3^{n-1}-1$

のように一般項が求められます．

≪変形のポイント≫
(2)式を(2’)式に変形するためのポイントは

$a_{n+1}-\alpha =3(a_n - \alpha)$

となる定数 $\alpha$ を係数比較によって求めることです．

$a_{n+1}=3(a_n - \alpha)+ \alpha$
$a_{n+1}=3a_n - 2\alpha$

を(2)式と係数比較すると

$- 2\alpha=2$
$\alpha=-1$

となって

$a_{n+1}+1=3(a_n+1)$ …(2’)

と変形できます．

　一般に，２項間漸化式が

$a_{n+1}=p a_n +q$

の形で与えられているとき

$a_{n+1}-\alpha=p(a_n -\alpha)$

となる定数 $\alpha$ は

$a_{n+1}=p(a_n -\alpha)+\alpha=p a_n+(1-p)\alpha$
を
$a_{n+1}=p a_n + q$
と係数比較することにより
$(1-p)\alpha=q$
$\alpha=\frac{q}{1-p}$ …(2”)
で求めることができます．（ $p\neq1$ が前提です）

次の項目→

※初歩的な注意として，次の点を押さえておきましょう．

□　この形の漸化式では $p\neq1$ が前提です． $p=1$ のときは，(2”)式において $\alpha$ が求められないことから気付きます．
　 $p=1$ のときは，≪階差形の漸化式≫という別の解き方を使います．

□　この形の漸化式について

$\alpha=p \alpha +q$

を特性方程式と呼び，その解 $\alpha$ を求めるという覚え方があります．
　これは，一般によく使われる解き方ですが，「特性方程式」や「その解」が何を表しているのかということを消化不良のまま使ってしまうと，危険な落とし穴にはまってしまう高校生が多いのです．

$\lbrac$ $a_1=1$
$a_{n+1}=3a_n+2$ …(2)

のような場合， $1, 5, 17, 53, \cdots$ となって，どこまで行っても $a_{n+1}$ と $a_n$ は等しくならない．

では，この方程式は何を解いているのか．
その解は何を表しているのか．

よく分からないままに，とりあえず真似をして $a_{n+1}$ と $a_n$ を両方とも $\alpha$ に置き換えたら特性方程式になるのだなと結果だけを覚えてしまうと

$a_{n+1}=a_n+1$ …(A) → $\alpha=\alpha+1$
としてしまう．
$a_{n+1}=2 a_n+n$ …(B) → $\alpha=2\alpha+ n$
としてしまう．
$a_{n+1}=n a_n$ …(C) → $\alpha=n\alpha$
としてしまう．

など，間違い答案がゾロゾロと登場します．(A)(B)(C)はいずれも特性方程式が使える場面でないところで使っています．
(A)は $p=1$ の場合なので，階差形の解き方を考えるべきです．(B)は特性方程式が $q$ が定数である場合にだけ使えるのに，その箇所に $n$ によって変化する項があるのに使っています．(C)は $p$ が定数である場合にだけ特性方程式が使えるのに，その箇所に $n$ によって変化する係数があるのに使っています．

２項間漸化式が， $p\neq 1$ ， $p, q$ とも定数の場合にしか使えない特性方程式を，適用できない場面で使ってしまうと無意味な答案になります．

　ここでは，(2)式を

$a_{n+1}-\alpha=3(a_n-\alpha)$

と変形できたらよいのにな～（等比数列になるから）と考えて

$a_{n+1}=3 a_n-2\alpha$
と
$a_{n+1}=3a_n+2$
と係数比較する

と考える方が誤解が少ないようです．

□　この考え方で行けば，(A)(B)(C)のような問題でも，工夫すれば解けます．

$a_{n+1}=a_n+1$ …(A) → $a_{n+1}+n+1=a_n+n$
→ $a_n+n$ は公比 $1$ の等比数列
→ $a_n+n=(a_1+1)\times 1^{n-1}=a_1+1$
→ $a_n=a_1+1-n$

$a_{n+1}=2 a_n+n$ …(B)
→ $a_{n+1}+n+2=2(a_n+n+1)$

→ $a_n+n+1$ は公比 $2$ の等比数列
→ $a_n+n+1=(a_1+ 2)\times 2^{n-1}$
→ $a_n=(a_1+ 2)\times 2^{n-1}-n-1$

$a_{n+1}=n a_n$ …(C)
→ $\frac{a_{n+1}}{n!}=\frac{a_n}{(n-1)!}$
→ $\frac{a_n}{(n-1)!}$ は公比 $1$ の等比数列

→ $\frac{a_n}{(n-1)!}=\frac{a_1}{0!}\times 1^{n-1}=a_1$
→ $a_n=a_1\times (n-1)!$

次の項目→

　≪この形の問題と解答≫
　次の漸化式で与えられる数列の一般項を求めてください．

番号	問題	解答	途中経過
(1)	$a_1=1$ $a_{n+1}=2 a_n$	$a_n=2^{n-1}$	[？]
(2)	$a_1=2$ $a_{n+1}=3a_n$	$a_n=2\times 3^{n-1}$	[？]
(3)	$a_1=2$ $a_{n+1}=2a_n+3$	$a_n=5\times 2^{n-1}-3$	[？]
(4)	$a_1=0$ $a_{n+1}+a_n=2$	$a_n=(-1)^n+1$	[？]
(5)	$a_1=2$ $a_{n+1}=\frac{a_n+ 2}{3}$	$a_n=\frac{1}{3^{n-1}}+1$	[？]
(6)	$a_1=1$ $2a_{n+1}-3a_n=1$	$a_n=2\times \left( \frac{3}{2} \right)^{n-1} -1$	[？]

次の項目→

(7)	$a_1=1$ $a_{n+1}=\frac{n+1}{n}a_n$	$a_n=n$	[？]
(8)	$a_1=1$ $a_{n+1}=(n+1)a_n$	$a_n=n!$	[？]
(9)	$a_1=0$ $a_{n+1}=2a_n+ n$	$a_n=2^n-n-1$	[？]
(10)	$a_1=0$ $a_{n+1}=2a_n+ n^2$	$a_n=3\times 2^{n-1}-n^2-2n-3$	[？]
(11)	$a_1=2$ $a_{n+1}=2 a_n+ 3^n$	$a_n=3^n-2^{n-1}$	[？]
(12)	$a_1=1$ $a_{n+1}=3a_n+ 2^{n-1}$	$a_n=2\times 3^{n-1}-2^{n-1}$	[？]

次の項目→

【問題】 …（簡単な再現問題です）
　次の漸化式で定義される数列の一般項を求めてください．（** HELPが必要なときは，上記の例と答を見てください **）
　はじめに左欄の定義式を選び，続いて右欄の一般項を選んでください．やり直すときは，右欄を連打するのでなく，左欄の問題を選び直すことから始めてください．

(1)