整数問題（入試問題）

→ スマホ用は別頁

=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには，次の色をクリック

◎内側の色を変えるには，次の色をクリック

◎標準文字色を変えるには，次の色をクリック

== 整数問題（入試問題） ==
［素数と因数分解］

【中学校数学の復習】
• 1よりも大きい整数のうちで，1とその数p自身の他に約数をもたない数pを素数という．
• 1は素数に含めない．
• 例えば，2, 3, 5, 7, 11, 13, 17, 19, ･･･などが素数である．
• 偶数の素数は2だけである．それ以外の素数3, 5, 7, 11, 13, 17, 19, ･･･などはすべて奇数である．

• 多項式が次の形に因数分解できるとき

(式１)×(式２)＝素数p
ただし，(式１)<(式２)
　　　ならば

(式１)=1，(式２)=p

と言える．これは，素数には1とその数p自身の他に約数がないからである．

大きな区分

高校数学 >> 高校数学Ⅰ・Ａ >> 整数問題

現在地と前後の項目

最大公約数，最小公倍数，ユークリッドの互除法/１次不定方程式の整数解/整数問題.センター(2015～)/ペル方程式/２進法,16進法,ｎ進法⇔10進法/N進法/２進数の演算/N進数の演算/N進数の小数/連続整数の積/累乗剰余/平方剰余/入試問題（素数,剰余類1）/入試問題（素数,剰余類2）/フェルマー予想,オイラー予想/3n+1問題(コラッツ予想)/

【例題1】
(1)　n3+1=pをみたす自然数nと素数pの組をすべて求めよ．
(2)　n3+1=p2をみたす自然数nと素数pの組をすべて求めよ．
(3)　n3+1=p3をみたす自然数nと素数pの組は存在しないことを証明せよ．

（2000年度千葉大）

（解答）
(1)
　(n+1)(n2−n+1)=p
と因数分解でき，nは自然数だからn+1≧2が成り立つ．したがって，

n2−n+1=1･･･①
n+1=p･･･②
①からn2−n=0
n(n−1)=0
nは自然数(≧1)だから
n=1
②から
p=2
結局，(n, p)=(1, 2)･･･（答）

(2)
　(n+1)(n2−n+1)=p2
と因数分解でき，nは自然数だからn+1≧2が成り立つ．したがって，
ア）

n2−n+1=1 (n≧1)･･･①
n+1=p2･･･②
または
イ）

n2−n+1=p (n≧1)･･･③
n+1=p･･･④
ア）のとき，①からn=1
　これを②に代入するとp2=2
　このような素数はないから，ア）からは解は求まらない
イ）のとき，④を③に代入してpを消去すると
n2−n+1=n+1
n2−2n=0
n(n−2)=0
n≧1だから
n=2
④に代入
p=3
結局，(n, p)=(2, 3)･･･（答）

(3)
　n3+1=p3 (n≧1)
を変形すると
　p3−n3=1
　(p−n)(p2+pn+n2)=1
ここでp2+pn+n2>0だから

p2+pn+n2=1･･･③
p−n=1･･･②
②を①に代入してnを消去すると
　p2+p(p−1)+(p−1)2=1
　p2+p2−p+p2−2p+1=1
　3p2−3p=0
　3p(p−1)=0
　p=0, 1
しかしpは素数であるから，解なし
以上により，与えられた条件をみたす自然数nと素数pの組は存在しない　■証明終わり■

（別解）
(1)(2)の解と同様にn3+1を因数分解して示してもよいが，その方法の場合は，n+1≧2も考えると，次のように場合分けが多くなる
　ア）n2−n+1=1, n+1=p3
　イ）n2−n+1=p, n+1=p2
　ウ）n2−n+1=p2, n+1=p
いずれも解は求まらない

【問題1.1】
　次の問いに答えよ．
f(n)=n4−2n2−3
(1)　f(n)をnの２次式の積で表せ．
(2)　nが自然数のとき，f(n)が素数となるnは１つだけ存在する．このときのnと素数f(n)を求めよ．

（2021年度北星学園大）

［解答を見る］

（解答）
(1)
f(n)=(n2−3)(n2+1)
(2)
　nは自然数だからn≧1, n2+1≧2
したがって，f(n)が素数となるには

n2−3=1･･･①
f(n)=n2+1が素数･･･②
①より
　n2=4
　n=2 (>0)
②に代入
　f(2)=22+1=5
以上から，n=2, f(n)=5･･･（答） →解答を隠す←

【問題1.2】
　x, yを自然数，pを3以上の素数とするとき，次の各問に答えよ．ただし，(1),(3)は答のみ記せ．
(1)　x2−y2=pが成り立つとき，x, yをpで表せ．
(2)　x3−y3=pが成り立つとき，pを6で割った余りが1となることを証明せよ．
(3)　x3−y3=pが自然数の解の組(x, y)をもつようなpを，小さい数から順にp1, p2, p3, ･･･とするとき，p5の値を求めよ．

（2014年度早稲田大学.政治経済学部）

［解答を見る］

（解答）
(1)
　(x+y)(x−y)=pでx, yは自然数だからx, y≧1, x+y≧2

x+y=p
x−y=1
を解くと

x = \frac{p + 1}{2}

y = \frac{p - 1}{2}

(2)
　(x−y)(x2+xy+y2)=pでx, yは自然数だからx, y≧1したがって,x2+xy+y2≧3

x2+xy+y2=p
x−y=1
だから
(x−y)2+3xy=p
1+3xy=p･･･(*)
ここでx−y=1だから，x, yは隣り合う奇数と偶数の組になる．したがって，xyは２の倍数
　結局，3xyは6の倍数になるから，pを6で割った余りが1となる．
(3)　(*)式に隣り合う整数を順に代入する

x=2
y=1

⇒ p1=1+3×2×1=7は題意に適する

x=3
y=2

⇒ p2=1+3×3×2=19は題意に適する

x=4
y=3

⇒ p3=1+3×4×3=37は題意に適する

x=5
y=4

⇒ p4=1+3×5×4=61は題意に適する

x=6
y=5

⇒ p=1+3×6×5=91=7×13は素数でない

x=7
y=6

⇒ p5=1+3×7×6=127は題意に適する

→解答を隠す←

【剰余類】
　例えば，すべての整数nは

ア）「3で割ったとき割り切れる」
イ）「3で割ったとき1余る」
ウ）「3で割ったとき2余る」

のいずれかに分類される．アイウは，3を法とする剰余類と呼ばれる．（剰余類の全体は剰余系と呼ばれる．）

　すべての整数nは，次のいずれかの形に書けると言ってもよい．kは整数とする．

ア） n=3k
イ） n=3k+1
ウ） n=3k+2（n=3k−1でもよい）

　高校の教科書には「合同式」や「mod」の記号や用語は，登場しないが，大学入試問題の解説ではよく使われる．高校生が答案に書くのは構わない．
　すべての整数nは，次のいずれかの形に書けると言ってもよい．

ア） n≡0　(mod 3)
イ） n≡1　(mod 3)
ウ） n≡2　(mod 3)

【例題2】

(1)　正の整数a, b, cが，a2+b2=c2を満たすとき，a, b, cのうち少なくとも１つは3の倍数であることを証明せよ．
(2)　正の整数a, b, cが，a2+b2=c2を満たすとき，a, b, cのうち少なくとも１つは5の倍数であることを証明せよ．
(3)　正の整数a, b, cが，a2+b2=c2を満たすとき，a, b, cのうち少なくとも１つは4の倍数であることを証明せよ．

（解答）
(1)
　k, K, L, M, Nは整数とする．
　正の整数は，3k, 3k±1のいずれかの形に書けるから，その２乗は9k2=3K, (3k±1)2=9k2±6k+1=3K+1の形に書ける．
　もし，a, b, cがいずれも3の倍数でなければ，

a2+b2=(3K+1)+(3L+1)=3M+2
c2=3N+1

となって，a2+b2とc2は，3で割ったときの余りが一致しないから，a2+b2=c2は成り立たない．
　背理法により，a2+b2=c2を満たすとき，a, b, cのうち少なくとも１つは3の倍数でなければならないことが示された．

(2)
　k, K, L, M, Nは整数とする．
　正の整数は，5k, 5k±1, 5k±2のいずれかの形に書けるから，その２乗は

25k2=5K
(5k±1)2=25k2±10k+1=5K+1
(5k±2)2=25k2+20k+4=5K+4

の形に書ける．
　もし，a, b, cがいずれも5の倍数でなければ，

a2+b2=(5K+1)+(5L+1)=5M+2
または
(5K+1)+(5L+4)=5M
または
(5K+4)+(5L+4)=5M+3

となって，5で割ったときの余りが，2,0,3のいずれかになる．
他方で，

c2=5N+1, 5N+4

となって，5で割ったときの余りが，1または4になる．
　このように，a2+b2とc2は，5で割ったときの余りが一致しないから，a2+b2=c2は成り立たない．
　背理法により，a2+b2=c2を満たすとき，a, b, cのうち少なくとも１つは5の倍数でなければならないことが示された．

(3)
　k, K, L, M, Nは整数とする．
　正の整数は，4k, 4k+1, 4k+2, 4k+3のいずれかの形に書けるから，その２乗は

(4k)2=16k2=8K
(4k+1)2=16k2+8k+1=8K+1
(4k+2)2=16k2+16k+4=8K+4
(4k+3)2=16k2+24k+9=8K+1

の形に書ける．
　もし，a, b, cがいずれも4の倍数でなければ，

a2+b2=(8K+1)+(8L+1)=8M+2
または
(8K+1)+(8L+4)=8M+5
または
(8K+4)+(8L+4)=8M

となって，8で割ったときの余りが，0,2,5のいずれかになる．
他方で，

c2=8N+1, 8N+4

となって，8で割ったときの余りが，1または4になる．
　このように，a2+b2とc2は，8で割ったときの余りが一致しないから，a2+b2=c2は成り立たない．
　背理法により，a2+b2=c2を満たすとき，a, b, cのうち少なくとも１つは4の倍数でなければならないことが示された．

（参考1）
　(3)の証明において，なぜ8の倍数の話が登場するのか？
　これは，初めから分かっていたのではなく，4の倍数で分類すると，4k+2の場合にうまく証明できないことから，4の剰余類で証明しようと考えていた方針を変更して「8の剰余類で分類することにした」ということです．
　一般に法を大きくすると剰余類も多くなるので，答案の場合分けが増える．だから，安易に法を大きくとるのは避けた方がよいが，やむを得ない場合もあるということは覚えておくとよい．

（参考2）
　上記の証明(1)(2)(3)によって，正の整数a, b, cが，a2+b2=c2を満たすのは

32+42=52

のように，１つずつ3,4,5の倍数に分かれてるということではない．
　少なくとも１つが3の倍数，4の倍数，5の倍数であるという条件を満たす組は

52+122=132

のように，１つの数12が3と4の倍数になっている場合や

112+602=612

のように，１つの数60が3,4,5の倍数になっていて，残り2つはどの倍数にもなっていないということもある．

【問題2.1】
　a, bを正の整数とする．aを6で割ると5余り，a2+bを6で割ると4余る.このとき，bを6で割ったときの余りは 7 であり，a2−b2を6で割ったときの余りは 8 である．

［ 7 に関する選択肢］

(ア) 1　　(イ) 2　　(ウ) 3　　(エ) 4　　(オ) 5

［ 8 に関する選択肢］

(ア) 1　　(イ) 2　　(ウ) 3　　(エ) 4　　(オ) 5

（2021年度獨協大）

［解答を見る］

（解答）
k, m, n, K, M, Nを整数とする．
　a=6k+5･･･①
　b=6m+r（0≦r≦5）･･･②
とおく．
　a2+b=(6k+5)2+(6m+r)
　=6K+25+(6m+r)=6M+(1+r)=6M+4
より
　r=3･･･(ウ)が答

　a2−b2=(6k+5)2−(6m+3)2
　=6K+25−(6M+9)=6N+4･･･(エ)が答
→解答を隠す←

【問題2.2】
　自然数aを3で割った余りをr=0, 1, 2とする．以下の問いに答えよ．
(1) 以下を求めよ．
（ア）r=0のとき，a3+4を3で割った余り．
（イ）r=1のとき，a3+4を3で割った余り．
（ウ）r=2のとき，a3+4を3で割った余り．
(2) 3つの自然数a, a3+4, a5+8のうちいずれか１つは3の倍数であることを示せ．
(3) 3つの自然数a, a3+4, a5+8が同時に素数となるaをすべて求めよ．

（2021年度中央大.理工学部）

［解答を見る］

（解答）
以下において，k, m, n, K, L, M, Nを整数とする．
(1)
（ア）r=0のとき

a3+4=(3k)3+4
=27k3+4=3(9k+1)+1=3K+1
だから，a3+4を3で割った余りは1･･･（答）

（イ）r=1のとき

a3+4=(3k+1)3+4
=3K+1+4=3(K+1)+2
だから，a3+4を3で割った余りは2･･･（答）

（ウ）r=2のとき

a3+4=(3k+2)3+4
=3K+8+4=3(K+4)
だから，a3+4を3で割った余りは0･･･（答）

(2)
a=3k, 3k+1, 3k+2のときのa, a3+4, a5+8を3で割った余りを表にすると次のようになる．

(*1)(*2)(*3)の簡単な理由は次の通り
(*1)←a=3kならばa5+8=3K+8=3L+2
(*2)←a=3k+1ならばa5+8=3K+1+8=3(K+3)=3L
(*3)←a=3k+2ならばa5+8=3K+8+8=3(K+5)+1=3L+1

a	3k	3k+1	3k+2
a3+4	3K+1	3K+2	3K
a5+8	3L+2 (*1)	3L (*2)	3L+1 (*3)

以上により，3つの自然数a, a3+4, a5+8のうちいずれか１つは3の倍数である．
(3)
a=3k, a3+4=3K, a5+8=3Lは，いずれも3の倍数であるから，素数となるのは3自体である場合のみになる．
　ところで，a3+4≧5, a5+8≧9だから，このうちで素数となることができるのは，a=3, (k=1)の場合だけである．
　このとき，a3+4=31, a5+8=251は素数．
　ゆえに，条件を満たすのはa=3･･･（答）

　a=251が素数であることを覚えている生徒はめったにいないと思うが，

\sqrt{251} = 15.84 . . .

だから，15以下の素数　{2, 3, 5, 7, 11, 13}で割ってみて，すべて割り切れなければ素数と判断すればよい．

→解答を隠す←

【問題2.3】

　3333の１の位の数を求めよ．

（名古屋大）

［解答を見る］

　整数の積や累乗の1の位の数は，1の位の数の積や累乗だけで決まり，十以上の位の数字に影響されないから，

760nの1の位の数字は0
981nの1の位の数字は1
125nの1の位の数字は5
356nの1の位の数字は6

などは直ちに言える．1の位の数が0,1,5,6以外である場合は，何乗かしてみると2乗または4乗ごとに循環していることが分かるので，それが利用できる．

1の位の数
n	2	3	4	7	8	9
n2	4	9	6	9	4	1
n3	8	7	4	3	2	9
n4	6	1	6	1	6	1
n5	2	3	4	7	8	9

　上記の表は，具体的に理解するには適しているが，証明となると･･･「この表から類推してください」では弱すぎる．（5乗よりも大きい累乗が書いてない）
　例えば，34=81=10k+1 （kは整数）だから
(34)n=10K+1（Kは整数）と変形すると楽に証明できる．

（解答）
34=81=10k+1 （kは整数）だから
(34)n=10K+1（Kは整数）
3333=(34)83×3=(10L+1)×3（Lは整数）
=10M+3（Mは整数）
よって，１の位の数は3･･･（答）
→解答を隠す←

【問題2.4】
　77777の１の位の数を求めよ．

（類題）

［解答を見る］

（解答）
74=2401=10k+1 （kは整数）だから
774=10K+1 （Kは整数）
これを使うと
77777=(774)194×7=(10K+1)194×7
=(10L+1)×7（Lは整数）
=10M+7（Mは整数）
よって，１の位の数は7･･･（答）
→解答を隠す←

【問題2.5】
　自然数x, yに対して，それぞれを100で割った余りが等しいとき,x≡yと書くことにする．
(1) 自然数mに対して，76m≡76を証明せよ．
(2) 2n≡76を満たす最小の自然数nを求めよ．
(3) 21001を100で割った余りを求めよ．

（2000年度名古屋大）

［解答を見る］

（解答）
(1) 762=5776≡76だから　763=762×76≡76×76≡76
同様にして，76m≡76m−1≡･･･≡76が言える
(2)

下２桁の位の数
n	1	2	3	4	5	6	7	8	9	10
2ⁿ	2	4	8	16	32	64	28	56	12	24

n	11	12	13	14	15	16	17	18	19	20
2ⁿ	48	96	92	84	68	36	72	44	88	76

　上記の表により,最小の自然数nは20
(3)
　21001=(220)50×2
　≡7650×2
　≡76×2=152
　≡52
100で割った余りは52 →解答を隠す←

【問題2.6】
　pが素数ならばp4+14は素数でないことを証明せよ．

（2021年度京都大.文系）

［解答を見る］

【秘訣⇒鉛筆遊びで傾向をつかむ】

p	2	3	4	5	6	7	8	9	10
p⁴	16	81	256	625	1296	2401	4096	6561	10000
p⁴+14	30	95	270	639	1310	2415	4110	6575	10014
3の剰余	0	2	0	0	2	0	0	2	0

• p, p⁴,p⁴+14, p⁴+14を３で割った余りを表にすると，上のようになる．
• 水色の背景色で示したように，pが3の倍数のとき，p⁴+14を３で割った余りは2になり，それ以外は3で割り切れる．
• 3で割り切れるものは素数でない．以上をまとめるとよい．

（解答）
　pは素数だから，p=3のときだけ３で割り切れ，それ以外のときは３で割り切れない．
ア） p=3のとき
　p4+14=81+14=95=5×19は素数でない
イ） pが3よりも大きな素数のとき
　p=3k±1　（kは整数）とおけるから
　p4+14=(3k±1)4+14=3N+1+14（Nは整数）
　=3(N+5)は3の倍数になり，素数ではない
　以上により，pが素数ならばp4+14は素数でないことが示された　■証明終わり■ →解答を隠す←

［解答を見る］

（別解）
　上記の答案では「３の剰余類で分類すればよい」というのが鍵になっていますが，「3」を思いつかなければどうなるのか⇒「5の剰余類で分類してもできる」ことを以下に示す

p	2	3	4	5	6	7	8	9	10
p⁴	16	81	256	625	1296	2401	4096	6561	10000
p⁴+14	30	95	270	639	1310	2415	4110	6575	10014
5の剰余	0	0	0	4	0	0	0	0	4

ア） p=5のとき
　p4+14=625+14=639=32×71は素数でない
イ） pが5以外の素数のとき
　p=5k±1, 5k±2　（kは整数）とおける
そのⅰ) p=5k±1のとき
　p4+14=(5k±1)4+14=5N+1+14（Nは整数）
　=5(N+3)は5の倍数になり，素数ではない
そのⅱ) p=5k±2のとき
　p4+14=(5k±2)4+14=5N+16+14（Nは整数）
　=5(N+10)は5の倍数になり，素数ではない
→解答を隠す←

【対偶証明の復習】
　元の命題p⇒qとその対偶q⇒pとは真偽が一致すること(*)を利用して，対偶q⇒pが真であることを示して，元の命題の証明とする方法

(*)の解説　　（1は真, 0は偽を表すものとする）

p⇒qの真偽(定義）
p	q	p⇒q
1	1	1
1	0	0
0	1	1
0	0	1

• 仮定pが真(1)で結論qが偽(0)の場合だけ，p⇒qは偽(0)と決める．それ以外の場合，p⇒qは真(1)

q⇒pの真偽
p	p	q	q	q⇒p
1	0	1	0	1
1	0	0	1	0
0	1	1	0	1
0	1	0	1	1

• 仮定qが真(1)で結論pが偽(0)の場合だけ，q⇒pは偽(0)になる．それ以外の場合，q⇒pは真(1)

• 上記の２つの表を見比べると，元の命題p⇒qとその対偶q⇒pとは真偽が一致することが分かる．

【対偶証明の例】
　x+y>0のとき，x, yの少なくとも１つは正の数であることを証明せよ．

　pが複合的な形をしていて，qが単純な形をしているとき，p⇒qを証明するよりも，その対偶q⇒pを証明する方が考えやすいことが多い．

（解答）
　x≦0かつy≦0のとき，x+y≦0となるから，対偶によって示される．

【背理法の復習】
　元の命題p⇒qをそのまま証明するのが難しいとき，pかつqを仮定すると矛盾を生ずることを示して，p⇒qの証明とする方法．

　対偶証明との相違点は，
「pも仮定する点」にある．
　証明の進め方によっては，q⇒pという対偶を一部として使用することも多いが，その場合は対偶によって証明できたと考えているのではなく，pとpが矛盾であることから，仮定が間違っていると述べるのが背理法．
　背理法の場合は，pに行き着く場合だけでなく，一般の数学的常識に反することに行き着けば何でもよい．例えば，1=2が導かれたり，2が奇数になったり，1>2が導かれるような場合はすべて矛盾であるから，対偶証明よりも背理法の方ができることが多い．

（別の見方）
　pという命題が成り立つ集合をPで表し，qという命題が成り立つ集合をQで表すとき，命題p⇒qには，集合の包含関係P⊂Qが対応する．
　P⊂Qであるとは，P∩Q（図の×印の部分）が空集合になること．
　したがって，P⊂Qを示すには，P∩Qとなるような要素xが存在すると仮定すると矛盾になるということを示せばよい．
　これが「p⇒qを背理法によって示す」ということを集合に対応させて考えたときの意味になる．

【背理法の例】
　自然数a, b, cがa2+b2=c2をみたすとき，a, bのうち少なくとも１つは3の倍数であることを証明せよ．

（解答）
　a2+b2=c2･･･(1)
　aもbも3の倍数でない･･･(2)
と仮定する
(2)より，a=3k±1, b=3m±1（k, mは整数）とおける
このとき，a2+b2=(3k±1)2+(3m±1)2
　=9k2±6k+1+9m2±6m+1
　=3N+2（Nは整数）･･･(3)
ところが，どんな自然数c=3p, 3p+1, 3p+2（pは整数）を持ってきても
　=c2=3N, 3N+1, 3N+1（Nは整数）
となって，(3)は成り立たない．
　以上により，(1)のときaもbも3の倍数でないと仮定すると矛盾を生ずる．
　背理法により，a, b, cがa2+b2=c2をみたすとき，a, bのうち少なくとも１つは3の倍数であることが証明された．

【例題3】
　a, b, cはa2−3b2=c2を満たす整数とするとき，次のことを証明せよ．
(1) a, bの少なくとも一方は偶数である．
(2) a, bが共に偶数なら，少なくとも一方は4の倍数である．
(3) aが奇数ならbは4の倍数である．

（2000年度東北大）

（解答）
(1)
a, bとも奇数と仮定すると，

a=2k+1, b=2m+1（k, mは整数）とおける．
このとき
a2−3b2=(2k+1)2−3(2m+1)2
=4k2+4k+1−3(4m2+4m+1)
=4k2+4k+1−12m2−12m−3
=4(k2+k−3m2−3m)−2
=4K−2･･･(*1)
この値とc2が等しいのだからcは偶数になる
そこで，c=2k（kは整数）と仮定すると
c2=4k2=4L･･･(*2)（Lは整数）
(*1)は左辺が4の倍数でないことを示しており，(*2)は右辺が4の倍数であることを示しているから，矛盾．
　背理法により，a, bの少なくとも一方は偶数であることが示された．

(2)
a2−3b2=c2･･･(*3)
a, bが共に偶数･･･(*4)

　(*4)により，a=2k, b=2m（k, mは整数）とおける．
　このとき，a2−3b2=4k2−12m2=4(k2−3m2)
　(*3)の右辺から，cは偶数でなければならない．
　そこで，c=2n（nは整数）とおくと右辺は
4n2となるから
4(k2−3m2)=4n2
k2−3m2=n2･･･(*5)
　(*5)に(1)の結果を適用すると，k, mの少なくとも一方は偶数になるから，a, bの少なくとも一方は4の倍数である．

(3)
(1)の結果を使って，aは奇数，bは偶数とすると，a2−3b2=c2により，cは奇数になる．

a=2k+1, b=2m, c=2n+1（k, m, nは整数）とおくと
(2k+1)2−3(2m)2=(2n+1)2
4k2+4k+1−3(4m2)=4n2+4n+1
4(k2+k−3m2)=4(n2+n)
k2+k−3m2=n2+n
k(k+1)−n(n+1)=3m2
ここで連続２整数の積は2の倍数だから，左辺のk(k+1), n(n+1)はいずれも2の倍数になり，その差も2の倍数
これが右辺の3m2に等しいのだから，mは偶数
よって，b=4p（pは整数）となり，bは4の倍数である．

【問題3.1】
(1) 任意の自然数aに対し，a2を3で割った余りは0か1であることを証明せよ．
(2) 自然数a, b, cがa2+b2=3c2を満たすと仮定すると，a, b, cはすべて3で割り切れなければならないことを証明せよ．
(3) a2+b2=3c2を満たす自然数a, b, cは存在しないことを証明せよ．

（2014年度九州大）

［解答を見る］

（解答）
(1)
ア） a=3k（kは整数）のとき

a2=(3k)2=9k2=3(3k2)=3K（Kは整数）
と書けるから，a2を3で割った余りは0

イ） a=3k±1（kは整数）のとき

a2=(3k±1)2=9k2±6k+1=3(3k2±2k)+1=3K+1（Kは整数）
と書けるから，a2を3で割った余りは1

アイ）より，任意の自然数aに対し，a2を3で割った余りは0か1である
(2)
ア） a, bの両方とも3で割り切れないとき

a=3k±1, b=3m±1（k, mは整数）とおけるから
a2+b2=3K+2（Kは整数）
となり，右辺の3c2と等しくならない

イ） a, bの一方が3で割り切れず，他方が3で割り切れるとき

a, b=3k, b=3m±1（k, mは整数）[順不同]とおけるから
a2+b2=3K+1（Kは整数）
となり，右辺の3c2と等しくならない

アイ）より，a, bの両方とも3で割り切れる．
さらに，このとき

a=3k, b=3m（k, mは整数）とおけるから
a2+b2=9K（Kは整数）
となり，右辺の3c2と等しくなるには，cが3で割り切れなければならない．

以上により，a, b, cはすべて3で割り切れなければならない．
(3)

(2)の結果を使うと，
a2+b2=3c2･･･①
⇒ a=3k1, b=3m1, c=3n1（k1,m1,n1は整数）･･･②
と書ける

これを代入すると
9k12+9m12=27n12
両辺を9で割ると

k12+m12=3n12･･･①'
⇒ k=3k2, m=3m2, n=3n2（k2,m2,n2は整数）･･･②'
と書ける

この作業をp回続けると（pは正整数）

a=3pk1, b=3pm1, c=3pn1（p, k1,m1,n1は整数）
と書けることになり，限りなく続けると，a, b, cとも無限大になり矛盾
　背理法により，これを満たす自然数a, b, cは存在しない

→解答を隠す←

（参考）･･･無限降下法
例えば，

\sqrt{2}

が無理数であることの証明を，通常は次のように行う．（受験生には必須の内容）

\sqrt{2}

が無理数であることを証明せよ．

（解答）

\sqrt{2} = \frac{n}{m}

（m, nは正整数で互いに素）とおく．

\sqrt{2} m = n

両辺を2乗する

2 m^{2} = n^{2}

･･･(1)
左辺は2の倍数であるから，右辺のn2も2の倍数でなければならないが，そのためにはnが2の倍数でなければならない．
n=2k（kは正整数）とおく･･･(2)
(1)に代入すると
2m2=4k2
両辺を2で割る
m2=2k2･･･(3)
(3)は，mも2の倍数であることを示している．
　以上から，m, nとも2の倍数であることになり「互いに素」という仮定に反する．
　

\sqrt{2} = \frac{n}{m}

（m, nは正整数で互いに素）という仮定から矛盾が導かれた．背理法により，

\sqrt{2}

は無理数である．

　以上のように，

\sqrt{2}

が無理数であることを示す背理法による標準的な証明は，初めの段階で「互いに素」という仮定を置くことにより，共通因数が１回登場した段階で証明を終ることができる．
　これに対して，「互いに素」という仮定を置かなければ，次のような記述になる．この論法は「無限降下法」と呼ばれ，フェルマーが大定理を証明するために用いた方法だと言われている（ただし，当時のフェルマーが実際に証明に成功していたかどうかは疑問とされている）

\sqrt{2} = \frac{n}{m}

（m, nは正整数）とおく．

\sqrt{2} m = n

2 m^{2} = n^{2}

･･･(1)

n = 2 n_{1}

(

n_{1}

は正整数,

1 ≦ n_{1} < n

)とおく･･･(1’)
(1)に代入すると

2 m^{2} = 4 n_{1}^{2}

両辺を2で割る

m^{2} = 2 n_{1}^{2}

･･･(2)

m = 2 m_{1}

(

m_{1}

は正整数,

1 ≦ m_{1} < m

)とおく･･･(2’)
(2)に代入すると

4 m_{1}^{2} = 2 n_{1}^{2}

両辺を2で割る

2 m_{1}^{2} = n_{1}^{2}

･･･(3)

n_{1} = 2 n_{2}

(

n_{2}

は正整数,

1 ≦ n_{2} < n_{1}

)とおく･･･(3’)
以上のように，(1)(1'),(2)(2'),(3)(3'),･･･のように変形していく作業は，限りなく繰り返すことができて，有限確定の正整数m, nについて次の不等式が成り立つことになる．

1 ≦ \dots < m_{3} < m_{2} < m_{1} < m

1 ≦ \dots < n_{3} < n_{2} < n_{1} < n

　これらは，有限確定の正整数m, nと1の間に無限個の整数が存在するという矛盾になっている．
　

\sqrt{2}

が有理数という仮定は間違っていることになり，背理法により，

\sqrt{2}

は無理数であることが証明された．

　2014年度九州大の問題(3)において，「a, b, cは正整数で互いに素」と仮定することができれば，上記のような無限降下法によらず，共通因数が１回登場すれば矛盾とすることができるはずであるが，(2)(3)の問題の組み立ての都合上，a, b, cとも3の倍数であるから「互いに素」と仮定することはできない．

【問題3.2】
(1) x2+4y2=9z2をみたす自然数x, y, zがあれば，xとyはいずれも3の倍数であることを示し，x2+4y2=9z2をみたす自然数x, y, zの例を挙げよ．
(2) x3+4y3=9z3をみたす自然数x, y, zは存在しないことを示せ．

（2014年度東京海洋大）

［解答を見る］

（解答）
(1)
x, yの少なくとも一方が3の倍数でない場合は，次の3つの場合に分けられる
ア）x=3k±1, y=3m±1 (k, mは整数)のとき

x2+4y2=(3k±1)2+4(3m±1)2
=3K+1+4(3M+1)=3(K+4M+1)+2
(K, Mは整数)
他方で，右辺は3の倍数だから，等式は成り立たない

イ）x=3k, y=3m±1 (k, mは整数)のとき

x2+4y2=(3k)2+4(3m±1)2
=3K+4(3M+1)=3(K+4M+1)+1
(K, Mは整数)
他方で，右辺は3の倍数だから，等式は成り立たない

ウ）x=3k±1, y=3m (k, mは整数)のとき

x2+4y2=(3k±1)2+4(3m)2
=3K+1+4(3M)=3(K+4M)+1
(K, Mは整数)
他方で，右辺は3の倍数だから，等式は成り立たない

以上により，x, yの少なくとも一方が3の倍数でなければ，x2+4y2=9z2は成り立たないから，x2+4y2=9z2をみたすときは，xとyはいずれも3の倍数でなければならない．

•

a^{2} + b^{2} = c^{2}

を満たす整数の組（ピタゴラス数）は限りなくあるが，上記の問題(1)の結果に沿って，a, bを各々3倍すればよい．［互いに素という条件はない］
•

3^{2} + 4^{2} = 5^{2} \to (3 \times 3)^{2} + (4 \times 3)^{2} = (5 \times 3)^{2}

\to (3 \times 3)^{2} + 4 (2 \times 3)^{2} = 9 \times 5^{2}

\to 9^{2} + 4 \times 6^{2} = 9 \times 5^{2}

•

5^{2} + 12^{2} = 13^{2} \to (5 \times 3)^{2} + (12 \times 3)^{2} = (13 \times 3)^{2}

\to (5 \times 3)^{2} + 4 (6 \times 3)^{2} = 9 \times 13^{2}

\to 15^{2} + 4 \times 18^{2} = 9 \times 13^{2}

• 「例を挙げよ」だから，簡単な例を１つ挙げればよい

9^{2} + 4 \times 6^{2} = 9 \times 5^{2}

だから
(x, y, z)=(9, 6, 5)･･･（答）

→解答を隠す←

［解答を見る］

(2)

x = 3 k \to x^{3} = 3 K

(k, Kは整数)

x = 3 k + 1 \to x^{3} = (3 k)^{3} + 3 (3 k)^{2} + 3 (3 k) + 1

=3K+1 (k, Kは整数)

x = 3 k + 2 \to x^{3} = (3 k)^{3} + 3 (3 k)^{2} (2) + 3 (3 k) 2^{2} + 2^{3}

=3K+2(k, Kは整数)
yについても同様
そこで，

x^{3} + 4 y^{3}

を3で割った余りは次の表のようになる

$x ∖ y$	3m	3m+1	3m+2
3k	0	1	2
3k+1	1	2	0
3k+2	2	0	1

• 例えば，表の2行3列目は，次のように埋まる

(k, K, m, M, Nは整数)

x = 3 k + 1 \to x^{3} = 3 K + 1

y = 3 m + 2 \to y^{3} = 3 M + 2

x^{3} + 4 y^{3} = 3 K + 1 + 4 (3 B + 2) = 3 N

• この表で，

x^{3} + 4 y^{3} = 9 z^{3}

･･･①を満たす可能性のあるものは，3で割り切れる値になるもので，赤枠で囲んだものとなる．さらにこれらの，ア）イ）ウ）の場合も成り立たないことが以下のように示される．
ア）x=3k, y=3mのとき

x^{3} + 4 y^{3} = 27 k^{3} + 4 \times 27 m^{3} = 27 (k^{3} + 4 m^{3})

= 9 z^{3}

となるから，z=3n(nは整数)でなければならない
　代入すると

27 k^{3} + 4 \times 27 m^{3} = 9 \times 27 n^{3}

　両辺を27で割ると

k^{3} + 4 m^{3} = 9 n^{3}

･･･②
②は①と同じ形をしているから，同様の議論により

k = 3 k_{1}, m = 3 m_{1}, n = 3 n_{1}

となる整数

k_{1}, m_{1}, n_{1}

が定まる．
　この作業を限りなく繰り返すと

1 ≦ \dots < k_{3} < k_{2} < k_{1} < k < x

1 ≦ \dots < m_{3} < m_{2} < m_{1} < m < y

1 ≦ \dots < n_{3} < n_{2} < n_{1} < n < z

のように，有限の整数値x, y, zと1の間に無限個の整数が入ることになり，矛盾
→解答を隠す←

［解答を見る］

イ）x=3k+1, y=3m+2 (k, mは整数)のとき

x^{3} + 4 y^{3}

= 27 k^{3} + 27 k^{2} + 9 k + 1 + 4 (27 m^{3} + 54 m^{2} + 18 m + 8)

= 9 K + 33 = 9 (K + 3) + 6

（Kは整数）
　　は9で割り切れないから，9z3に等しくならない
ウ）x=3k+2, y=3m+1 (k, mは整数)のとき

x^{3} + 4 y^{3}

= 27 k^{3} + 54 k^{2} + 18 k + 8 + 4 (27 m^{3} + 27 m^{2} + 9 m + 1)

= 9 K + 12 = 9 (K + 1) + 3

（Kは整数）
　　は9で割り切れないから，9z3に等しくならない

　以上のように，ア）イ）ウ）いずれの場合も成り立たないから，x3+4y3=9z3をみたす自然数x, y, zは存在しない →解答を隠す←

【問題3.3】
　a−b−8とb−c−8が素数となるような素数の組
(a, b, c)をすべて求めよ．

（2014年度一橋大）

［解答を見る］

• 偶数の素数は2だけ．他の素数(3, 5, 7, ...)は奇数

（解答）
a>b+8, b>c+8だから
c<b<a
ア） a, b, cのいずれも奇数のとき

a−b, b−cは偶数で，a−b−8とb−c−8も偶数になる．
偶数の素数は2だけだから

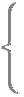a−b−8=2
b−c−8=2
すなわち

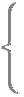a−b=10
b−c=10

ただし，a, b, cは奇数でc<b<a

これに適する解として，c=3, b=13, a=23を思い着く

これ以外の組をどう処理するか←これが鍵
（試験会場で鉛筆遊びからスタート）：赤字は素数でない

c=1,b=11,a=[21]
c=11,b=[21],a=31
c=[21],b=31,a=41
c=31,b=41,a=[51]

c=[3],b=13,a=23
c=13,b=23,a=[33]
c=23,b=[33],a=43
c=[33],b=43,a=53

c=5,b=[15],a=25
c=[15],b=25,c=35
ここは全部ダメ

c=7,b=17,a=[27]
c=17,b=[27],a=37
c=[27],b=37,a=47

c=[9],b=19,a=29
c=19,b=29,a=[39]
c=29,b=[39],a=49

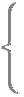a−b=10
b−c=10

ただし，a, b, cは奇数でc<b<a

を満たす組は無限にあるが，上記の鉛筆遊びから分かるように，どの組にも[ ]で示した３の倍数が含まれる．
⇒3以外の3の倍数は素数でないから，他の組は条件に合わないと言えばよい．

→解答を隠す←

［解答を見る］

ア）の続き
(ⅰ) c=3k（kは整数）のとき，条件に合う組はc=3, b=13, a=23だけである．
(ⅱ) c=3k+1（kは整数）のとき
　b=3k+11, a=3k+21=3(k+7)となって，aが素数でない
(ⅲ) c=3k+2（kは整数）のとき
　b=3k+12=3(k+4), a=3k+22となって，bが素数でない
以上から，条件に合う組はc=3, b=13, a=23だけである．

イ） c=2だけ偶数でa, bは奇数のとき

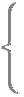a−b−8=2
b−2−8が素数
すなわち

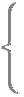a=b+10･･･①
b−10=dが素数･･･②
c=2, b=13, a=23は条件に合う
(ⅰ) b=3k（k≧1は整数）のとき，bが素数となるのはb=3ときだけであるが，このときは②のdが負の数になり，適さない
(ⅱ) b=3k+1（k≧1は整数）のとき
　a=3k+11, d=3k+1−10=3(k−3)となって，k=4の場合のみd=3が素数になる
これはc=2, b=13, a=23ですでに登場している
(ⅱ) b=3k+2（k≧1は整数）のとき
　a=3k+12=3(k+4)は素数でない

アイ）より，結局(23, 13, 3), (23, 13, 2)･･･（答） →解答を隠す←

【定着度チェック問題】･･･このページの振り返りです

【問題4.1】･･･受験では基礎のレベル
　整数a, bについて，aは13で割ると2余り，bは13で割ると7余る．このとき，4a+3bは13で割るとタ余り，abは13で割るとチ余る．

（2021年度金沢工大）

［解答を見る］

a=13k+2, b=13m+7（k, mは整数）とおく
このとき
　4a+3b=4(13k+2)+3(13m+7)=13(4k+3m)+29
　=13(4k+3m+2)+3
だから，13で割ると3余る→[タ]
　ab=(13k+2)(13m+7)
　=132km+13×7m+13×2m+14
　=13(K+1)+1（Kは整数）
だから，13で割ると1余る→[チ]
→解答を隠す←

【問題4.2】･･･ちょうど良いレベルの良問
(1) k2+2が素数となるような素数kをすべてみつけよ．また，それ以外にないことを示せ．
(2) 整数lが5で割り切れないとき，l4−1が5で割り切れることを示せ．
(3) m4+4が素数となるような素数mは存在しないことを示せ．

（2021年度お茶の水女子大）

［解答を見る］

(1)

• k=3m±1→k2=3M+1 →■よく出るから，使えるようにしておく!!■← →k2+2=3(M+1)だから，「3で割って1余る数」や「3で割って2余る数」に対してk2+2は素数にならない
• しかし，k=3mとなる数（3の倍数）の中に１つだけ素数がある．

ア） k=3m+1（m≧1は整数）のとき
　k2=9m2+6m+1=3M+1（M≧5は整数）
　だからk2+2=3(M+1) (≧18)は素数でない
イ） k=3m+2（m≧0は整数）のとき
　k2=9m2+12m+4=3M+1（M≧1は整数）
　だからk2+2=3(M+1) (≧6)は素数でない
ウ） k=3m（m≧1は整数）のとき
　k2+2=9m2+2 (≧11)
　はk=3のとき，k2+2=11が素数になる．
k=3･･･（答）
→解答を隠す←

［解答を見る］

(2)
　5で割り切れない整数lは，l=5k±1, 5k±2（kは整数）とおける．
　展開公式(x+y)4=x4+4x3y+6x2y2+4xy3+y4を使うと
ア）l=5k±1（kは整数）のとき
　l4=(5k±1)4=(5k)4±4(5k)3+6(5k)2±4(5k)+1=5K+1
　　　（Kは整数）とおけるから
　l4−1=5Kは5で割り切れる
イ）l=5k±2（kは整数）のとき
　l4=(5k±2)4
　=(5k)4±4(5k)3(2)+6(5k)2(22)±4(5k)(23)+16=5K+16
　=5(K+3)+1
　　　（Kは整数）とおけるから
　l4−1=5Kは5で割り切れる
ア）イ）から，整数lが5で割り切れないとき，l4−1が5で割り切れる →解答を隠す←

［解答を見る］

m4+4=(m2+2)2−(2m)2=(m2−2m+2)(m2+2m+2)
ここで，mを素数（≧2）とすれば，
　m2−2m+2 < m2+2m+2
　m2−2m+2=(m−1)2+1≧2
となるから，m4+4=(m2−2m+2)(m2+2m+2)は2以上の整数の積になり，素数でない
→解答を隠す←

【問題4.3】･･･チャレンジしてみよう
　素数p, qを用いて pq+qp と表される素数をすべて求めよ．

（2016年度京都大）

［解答を見る］

• 偶数の素数は2だけ．他の素数(3, 5, 7, ...)は奇数

（解答）
　次の4つの場合に分けて求める．
ア）p, qとも偶数のとき

偶数の素数は2だけだから，p=2, q=2とおくと，pq+qp=4+4=8は素数でないから，適さない

イ）p, qとも奇数(≧3)のとき

pq+qp (≧33+33≧54)は奇数と奇数の和で偶数になる．ところが，偶数の素数は2だけで，54以上のものはない

ウ）pが偶数，qが奇数のとき

偶数の素数は2だけだから，p=2とおくと，2q+q2が素数となるかどうか調べる．
ここで，q=6k+1, 6k+3, 6k+5(kは整数)について，次の場合分けに沿って，3で割った余りを求める．
• q=6k+3=3(2k+1)(kは整数)となる場合で，qが素数となるのはq=3だけ
このとき，2q+q2=8+9=17は素数
• q=6k+1(k≧1は整数)のとき,
22=4 (=3m+1)(mは整数)だから
26k+1=(22)3k×2=3L+2 (L≧1は整数)
q2=(6k+1)2=3M+1 (M≧1は整数)
したがって，2q+q2=3L+2+3M+1=3(L+M+1)は3の倍数になるが，3よりも大きな素数はない
• q=6k+5(k≧1は整数)のとき,
22=4 (=3m+1)(mは整数)だから
26k+5=(22)3k+4×2=3L+2 (L≧1は整数)
q2=(6k+5)2=3M+25=3(M+8)+1 (M≧1は整数)
したがって，2q+q2=3L+2+3(M+8)+1=3(L+M+9)は3の倍数になるが，3よりも大きな素数はない

エ）pが奇数，qが偶数のとき

ウ）の場合とp, qを入れ替えたものになる

以上から，(p, q)=(2, 3), (3, 2)でpq+qp=17･･･（答） →解答を隠す←

【問題4.4】
　nを2以上の整数とする．3n−2nが素数ならばnも素数であることを示せ．

（2021年度京都大）

［解答を見る］

（解答）
　対偶証明によって示す．
　nが素数でないと仮定すると，n=pq（p, qは2以上の整数）とおける．

因数分解公式
an−bn=(a−b)(an−1+an−2b+an−3b2+･･･+bn−1)を使うと
3pq−2pq=(3p)q−(2p)q
=(3p−2p){(3p)q−1+(3p)q−2(2p)+(3p)q−3(2p)2+･･･+(2p)q−1}
　p, qは2以上の整数だから
• (3p)q−1+(3p)q−2(2p)+(3p)q−3(2p)2+･･･+(2p)q−1>1は明らか
• 3p−2p>1は次のように数学的帰納法で示せる．
(Ⅰ) p=2のとき
　3p−2p=9−4=5>1は成り立つ
(Ⅱ) p=k (k≧2)のとき
　3k−2k>1が成り立つと仮定すると
　3k+1−2k+1=3(3k−2k)+3×2k−2k+1
=3(3k−2k)+(3−2)2k
=3(3k−2k)+2k≧3+4>1
(Ⅰ)(Ⅱ)より，2以上の整数pについて，3p−2p>1が成り立つ．
以上により，nが素数でなければ，3n−2nが素数でないことが示されたから，対偶証明により，3n−2nが素数ならばnも素数であるといえる．

→解答を隠す←

...（PC版）メニューに戻る

■このサイト内のGoogle検索■

△このページの先頭に戻る△【アンケート送信】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．

○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）

質問に対する回答の中学版はこの頁，高校版はこの頁にあります