|
[I] 共通に割れるだけ割っていく方法 最大公約数を求める1つの方法は,共通な数で割れるだけ割っていく方法です. このとき,共通に割れる数の積が最大公約数です. 最小公倍数を求める方法は,これと同様ですが,割った数と残った数を掛けます. 例 次の例で,12 , 18 の最大公約数は 6,18 , 27 の最大公約数は 9 です. 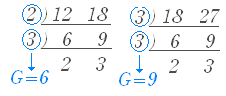 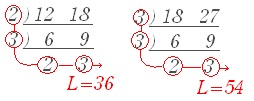 |
【問題1】
2数42, 28の最大公約数G,最小公倍数Lを求めてください.(正しい組合せを選んでください.) 1G=2, L=1176 2G=7, L=70 3G=14,L=84 4G=14,L=168 HELP 2
) 42 , 28
7
) 21 , 14
3
2
G=2×7=14 L=2×7×3×2=84 →3
【問題2】
2数60, 72の最大公約数G,最小公倍数Lを求めてください.(正しい組合せを選んでください.) 1G=12, L=60 2G=12, L=360 3G=60, L=360 4G=60, L=4320 HELP 2
) 60 , 72
6
) 30 , 36
5
6
G=2×6=12 L=2×6×5×6=360 →2
|
||||
|
3つ以上の数について最大公約数と最小公倍数を求めるときは,「共通に割れる」という言葉の意味が変わります.最大公約数を求めるときには,「全部に共通」に割り切れなければ進んではいけませんが,最小公倍数を求めるときには,「一部でも割れたら割り」,他はそのまま残します. 例
(参考)
〇次のプログラムは,3つの数A,B,Cの最大公約数Gと最小公倍数Lを求めるものです.3つの空欄(各々7桁以下の整数とします.)を埋めてボタンを押してください. |
【問題3】
次の計算をもとにして,3数24, 36, 54の最大公約数を求めてください. 2
) 24 , 36 , 54
3
) 12 , 18 , 27
4
6
9
12 23 36 412 436 HELP
G=2×3=6
→3
【問題4】
次の計算は,3数4, 6, 9の最小公倍数を求める計算の途中経過を示したものです.x, yに当てはまる数を答えてください. 3
) 4 , 6 , 9
2
) x , 2 , 3
2
1
y
1x=4/3, y=3/2 2x=1, y=1 3x=2, y=3 4x=4, y=3 HELP
6と9が3で割り切れるので,各々2と3にしますが,そのとき4は3で割り切れないので,4のまま下げます.
x=4 4と2が2で割り切れるので,各々2と1にしますが,そのとき3は2で割り切れないので,3のまま下げます. y=3 →4
|

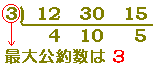
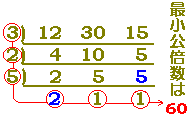
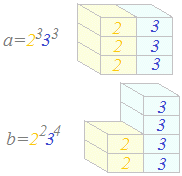 例えば,
例えば,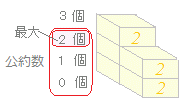 このように,公約数の中で最大のものは,
このように,公約数の中で最大のものは,

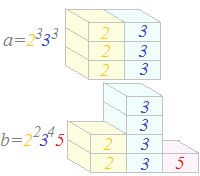 (解説)
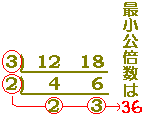
(解説)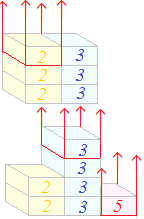 このように,公倍数の中で最小のものは,
このように,公倍数の中で最小のものは,