|
=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには,次の色をクリック
基 本:★☆☆
普 通:★★☆
やや難:★★★
|
→ スマホ用は別頁
|
|
=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには,次の色をクリック
基 本:★☆☆
普 通:★★☆
やや難:★★★
|
→ スマホ用は別頁
|
|
【領域における最大・最小問題】
• 高校数学で扱う「領域における最大・最小問題」は,下記の例題1のように「領域がx, yの連立1次不等式で表され」「最大値・最小値を求めたい式がx, yの1次式で与えられる」ものが基本です. 例えば,「x+yの最大値・最小値を求めなさい」という問題が与えられたとき,x+yという「式だけ」では図が対応しないが,x+y=kとおくと直線の「方程式」となって,グラフが描けます. このように,与えられた領域内でグラフを描いて,kの値が最大・最小となる点を探すというのが,この種の問題の解き方の流れです. |
• 幾つか問題を解けばすぐ分かることですが「領域がx, yの連立1次不等式で表され」「最大値・最小値を求めたい式がx, yの1次式で与えられる」問題では,最大値・最小値は必ず多角形の頂点で求まります.
一般に,n変数の連立不等式で定まる範囲内で,n変数で与えられる式の最大・最小を求める問題は「線形計画法の問題」と呼ばれ,解は領域を表す多角形の頂点から求まります. |
|
【例題1】★☆☆
x, yが3つの不等式 (2016年度関西学院大 経済学部他[一部引用])
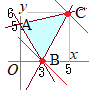 条件を満たす領域は右図の水色で示した部分(内部および周上)
条件を満たす領域は右図の水色で示した部分(内部および周上)交点の座標は2つずつ選んだ連立方程式の解として求められ,A(0, 5), B(3, 0), C(5, 6)となる. • x+y=kすなわち,y=−x+kとおくと,傾きが−1の直線になるから,右図で赤線で示したように 点B(3, 0)において最小値3+0=3をとる. 点C(5, 6)において最大値5+6=11をとる.・・・(答) (雑談のようで雑談ではない話)・・・本気の授業 上の答案でx+y=kの直線が通っていると言っても,最大値となる点はCの1つしかない.最小値の方も同様にBが1つだけ.・・・こんな頼りない話でよいのか?と思うかもしれませんが,この点に目を向けると,領域内の最大最小問題に鋭く切り込んでいける. 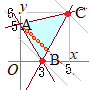 --図1--
--図1--
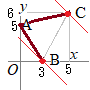 --図2--
--図2--
例えば,図1の点A(0, 5)を通るとき,x+y=0+5=5となって,最大値11と最小値3の間の1つの値となっている.ところが,点A(0, 5)を通るx+y=5となる点は,この領域の中に沢山ある(外赤.中黄で示した).(1, 4), (2, 3), (3, 2), ...などどの点で調べてもx+y=5となる. 実は,この問題で領域の内部は無くても結果に影響しない・・・図2のように,B-A, A-Cの「線だけ,皮だけ」の部分でも「最大値11,最小値3,およびその間のすべての値」はとり得ることに注意. このように「ある値がとり得るか?」という問題に対しては,点が1つあれば十分 |
【問題1】★☆☆
[解説を読む]次の連立不等式 3x+2y≧12, 2x+3y≦18, x−y≦4
をみたすx, yの値に対して,x+yのとる値の最大値はコ,最小値はサである.
(2005年度東洋大 工学部)
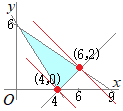 条件を満たす領域は,右図の水色で示した部分(内部および周上)
条件を満たす領域は,右図の水色で示した部分(内部および周上)x+y=k すなわち y=−x+k とおくと,傾きが−1の直線になる. 3x+2y=12の傾き 2x+3y=18の傾き と比較すると,傾き−1は,右下がりで, |
|
• 下記の例題2のように「領域がx, yの連立1次不等式で表されるが」「最大値・最小値を求めたい式がx, yの2次式などで与えられる」ときには
(1)
⇒
(2) xyの最大値・最小値
⇒ xy=kとおく.直角双曲線(中学1年生で習う反比例のグラフ)でkの値が最大・最小となる点を探せばよい.
【例題2】★★☆
実数x, yが3つの不等式 x−2y−1≦0, 2x+y−2≦0, 4x−3y+6≧0 を満たすとき,x2+y2の最大値,最小値を求めよ. 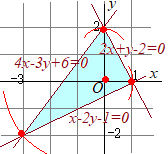 条件を満たす領域は右図の水色で示した部分(内部および周上)
条件を満たす領域は右図の水色で示した部分(内部および周上)
• x−2y−1=0と2x+y−2=0の交点は(1, 0)
x2+y2は原点からの距離(の2乗)だから,• 2x+y−2=0と4x−3y+6=の交点は(0, 2) • 4x−3y+6=0とx−2y−1=0の交点は(−3, −2) • 原点(0, 0)において最小値0をとる • 点(−3, −2)において,最大値13をとる・・・(答) |
【問題2】★☆☆
[解説を読む]x, yが3つの不等式 (2016年度関西学院大 経済学部他[一部引用])
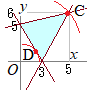 条件を満たす領域は右図の水色で示した部分(内部および周上)
条件を満たす領域は右図の水色で示した部分(内部および周上)この距離が最小となる点Dは,点と直線の距離の公式を用いて求められる.
• 原点(0, 0)から直線5x+3y−15=0に引いた垂線の長さは
点(x0, y0)から直線ax+by+c=0に引いた垂線の長さは
最小値は
直線5x+3y−15=0と円直線x2+y2=kが接する条件を判別式で求める場合は
• x, yの値は,について判別式をDとおくと を解くと得られる. |
|
【問題3】★☆☆
[解説を読む]xy平面上の点A, B, Cの座標は,それぞれ (1, 1), (3, 1), (2, 3)である.三角形ABCの内部および境界で与えられる領域をDとする.以下の問いに答えよ. (1) 領域Dを図示し,不等式を用いて表せ. (2) 点(x, y)が領域D内を動くとき,4x+yの最大値と最小値を求めよ. (3) 点(x, y)が領域D内を動くとき, (2021年度長崎大 情報データ科学部)
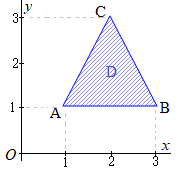 (1)
(1)右図の青色で示した斜線部の内部および境界線上 (2) 4x+y=k すなわち y=−4x+k とおくと,傾きが−4の直線(赤で示した直線)になる. 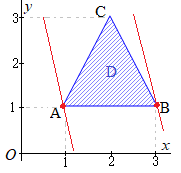
そのうちで,点A(1, 1)を通るとき,最小値4x+y=5をとり,点B(3, 1)を通るとき,最大値4x+y=13をとる. (3) 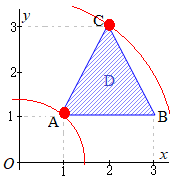
|
【問題4】★☆☆
[解説を読む]連立不等式y≦x−2, y≧2x−8, y≧0を満たす領域の点(x, y)についてx2+(y−4)2の最小値と最大値,およびそれらを与える(x, y)の値を求めよ. (2021年度三重大 教育学部)
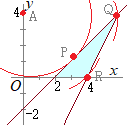 連立不等式の表す領域は,右図の水色で示した箇所
連立不等式の表す領域は,右図の水色で示した箇所x2+(y−4)2=kとおくと,kは 点(0, 4)からの距離の2乗を表す. 右図の点Pは,点A(0, 4)を中心とする円と直線y=x−2すなわちx−y−2=0が接する場合の接点で k=AP2=18・・・(最小値:答) 右図の点Qは,2直線y=x−2, y=2x−8の交点(6, 4)で k=AQ2=62=36 右図の点Rは2直線y=2x−8, y=0の交点(4, 0)で AQ>ARだから,最大値はk=AQ2=62=36・・・(答) |
|
【問題5】★★☆
[解説を読む]実数x, yが3つの不等式 y≦2x, y≦−2x+4, y≧0 を満たすとき,x2+y2−4x+2yの最大値,最小値を求めよ. 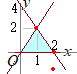 条件を満たす領域は右図の水色で示した部分(内部および周上)
条件を満たす領域は右図の水色で示した部分(内部および周上)x2+y2−4x+2y=kとおくと (x−2)2+(y+1)2=k+5だから,kは点(2, −1)からの距離の2乗(+5) • 点(2, 0)において最小値−4をとる • 点(1, 2)において,最大値5をとる・・・(答)
【問題6】★★☆
[解説を読む]実数x, yが3つの不等式 y≦2, x+y≧2, x≦2 を満たすとき, 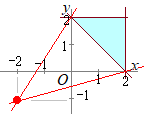 条件を満たす領域は右図の水色で示した部分(内部および周上)
条件を満たす領域は右図の水色で示した部分(内部および周上)すなわち とおくと,kは,点(−2, −1)を通る直線の傾き • 点(2, 0)において最小値 • 点(0, 2)において最大値 |
【問題7】★★☆
[解説を読む]実数x, yが3つの不等式 y≦3x−2, 2y≧x+1, y≦−2x+8 を満たすとき, 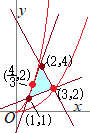 条件を満たす領域は右図の水色で示した部分(内部および周上)
条件を満たす領域は右図の水色で示した部分(内部および周上)
• y=3x−2と2y=x+1の交点は(1, 1)
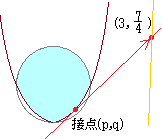
• y=3x−2とy=−2x+8の交点は(2, 4) • 2y=x+1とy=−2x+8の交点は(3, 2) すなわち とおくと,kの値は • 点(3, 2)において,最小値 • y=3x−2とy=kx2が接するとき,最大値をとる.
このとき
以上から,3x−2=kx2 (k≠0) kx2−3x+2=0 (k≠0) D=9−8k=0 このときの接点が,実際に直線y=3x−2上にあって,2点(1, 1), (2, 4)の間にあることは,次のように示せる. kx2−3x+2=0は 9x2−24x+16=0となり (3x−4)2=0を解くと このとき,y=3x−2=2 だから,実際に直線y=3x−2上にあって,2点(1, 1), (2, 4)の間にある |
|
【問題8】★★☆
[解説を読む]連立不等式 (2016年度学習院大 経済学部)
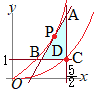 条件を満たす領域は右図の水色で示した部分(内部および周上)
条件を満たす領域は右図の水色で示した部分(内部および周上)すなわち とおくと,kの値は • 点 • y=2x−2とy=kx2が接するとき,最大値をとる.
このとき
以上から,点P(2, 2)において最大値2x−2=kx2 (k≠0) kx2−2x+2=0 D’=1−2k=0 このときの接点Pが,実際に直線y=2x−2上にあって,2点 kx2−2x+2=0は x2−4x+4=0となり (x−2)2=0を解くと x=2(重解) このとき,y=2x−2=2 だから,実際に直線y=2x−2上にあって,2点 |
【問題9】★★☆
[解説を読む]点(x, y)がx≧0, y≧0, 3≧x+y≧1を満たすとき,xy+2x+yの最大値と最小値を求めよ. 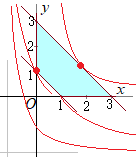 条件を満たす領域は右図の水色で示した部分(内部および周上)
条件を満たす領域は右図の水色で示した部分(内部および周上)xy+2x+y=k とおくと (x+1)(y+2)=k+2 は,漸近線の方程式がx=−1, y=−2となる直角双曲線で k+2の値,したがってkの値は, (0, 1)のとき最小値1をとる. (2, 1)のとき最大値7をとる.・・・(答) |
|
【問題10】★☆☆
[解説を読む]x, yが不等式x≧0, y≧0, 2x+3y≦18, x+3y≦15を同時に満たすとき,次の(1)〜(3)に答えよ. (1)(2) 略 (3) xyの最大値を求めよ. (2005年度福井県立大)
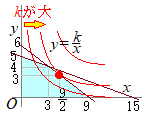 条件を満たす領域は,右図の水色で示した部分(内部および周上)
条件を満たす領域は,右図の水色で示した部分(内部および周上)この領域内において,xy=kすなわち のグラフを考える. xy=kと2x+3y=18が接するようなkの値を求める. |
• 下記の問題11のように,領域の境界線が2次曲線(円・放物線・双曲線など)で表されているときは,最大・最小となる点を求めるために,「判別式=0」の関係がよく使われます.
【問題11】★☆☆
[解説を読む]実数x, yがx2+y2≦2を満たすとき,5x+yの最大値および最小値を求めなさい. (2016年度福島大 人文社会学部)
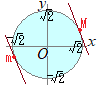 条件を満たす領域は右図の水色で示した部分(内部および周上)
条件を満たす領域は右図の水色で示した部分(内部および周上)5x+y=kすなわちy=−5x+kとおくと,傾きが−5の直線を表す. 右図の領域の中で,kの値は,円と直線が接するときに最大および最小となる. y=−5x+k この連立方程式から,yを消去して,xの2次方程式の判別式を求める.
x2+(−5x+k)2=2
最大値26x2−10kx+(k2−2)=0 |
|
【問題12】★☆☆
[解説を読む]連立不等式
y≧x2−1 の表す領域をDとおく.
(1) 領域Dの概形を図示せよ. (2) 直線y=k(x+2)−2とDが共有点をもつときの直線の傾きkのとりうる値の範囲を求めよ. (2016年度東北大 経済学部[後期])
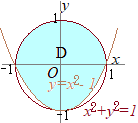 (1)
(1)右図の右図の水色で示した部分(内部および周上) なお,2つの曲線は(±1, 0), (0, −1)の3点を共有点とするが, −1<x<0, 0<x<1の区間で
(根拠1)
(根拠2) 0<x<1のとき だから 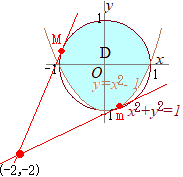 (2)
(2)y=k(x+2)−2は点(−2, −2)を通り,傾きkの直線だから,kのとりうる値の範囲は,右図のような2つの接線から求められる. ア)y=k(x+2)−2とx2+y2=1の上半円が接する場合:最大値M kx−y+(2k−2)=0と原点(0, 0)との距離が1になること このうちで大きい方が上半円との接点の傾きを表すから イ)y=k(x+2)−2とy=x2−1が接する場合:最小値m x2−1=k(x+2)−2 x2−kx+(1−2k)=0 図から考えて,符号が正の方を選ぶと 以上から, |
【問題13】★★☆
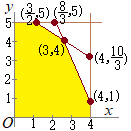
[解説を読む]xy平面上で,連立不等式 y≧0, x+y≦4, 3x+y≦6, y−2x≦6 が表す領域をDとする.このとき,次の問いに答えよ. (1) 領域Dを図示せよ. (2) 点(x, y)が領域D上の点全体を動くとき,x+2yの最大値とそのときのx, yの値を求めよ.また,x+2yの最小値とそのときのx, yの値を求めよ. (3) 点(x, y)が領域D上の点全体を動くとき,3x2−2yの最大値とそのときのx, yの値を求めよ.また,3x2−2yの最小値とそのときのx, yの値を求めよ. (2021年度同志社大 文学部・経済学部)
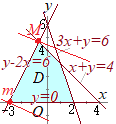 (1) 右図の水色で示した部分
(1) 右図の水色で示した部分(内部および周上) (2) x+2y=kとおくと, また,mで示した点(−3, 0)で最小値−3をとる. (3) 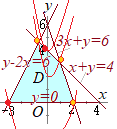 3x2−2y=kとおくと,
3x2−2y=kとおくと,• 点(−3, 0)で最大値k=3x2−2y=27をとる • 直線x+y=4と3x2−2y=kが接するとき,最小値をとる.
判別式を使って,接するときのk, x, yの値を求める
よって,3x2−2(4−x)=k 3x2+2x−(8+k)=0 D’=1+3(8+k)=0 3k=−25 このとき 9x2+6x+1=0 (3x+1)2=0 |
|
【問題14】★★★
[解説を読む](1) 座標平面上の点(x, y)と点(a, b)を結ぶ線分の傾きを求めよ.ただし,x≠aとする. (2) 次の連立不等式の表す領域Dを図示せよ. x2+y2≦1, y≧x2−1 (3) (2)の領域D内の点(x, y)に対して (2011年度津田塾大 学芸学部数学科)
 (1)
(1)(2) 右図の水色で示した部分(内部および周上) (3)
「
と変形できるから,領域Dにおいて,点 (解法1)・・・微分を習っている場合 接点の座標を(p, p2−1)とおいて,接線が点
y=x2−1
だから,(p, p2−1)における接線の方程式はy’=2x
y−(p2−1)=2p(x−p)
この接線が点(※黄色で示した接線は,領域Dを通らない) このとき, 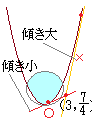 (解法2)・・・接する条件を判別式で求める場合
(解法2)・・・接する条件を判別式で求める場合が接するようにmの値を定める.
yを消去する
このときの接点(x, y)を求める判別式を求める 小さい方を選んで m=1 |
【問題15】★☆☆
[解説を読む]薬品AとBを合成して製品XとYを作る.Xを1トン作るにはAが2トンとBが3トン,Yを1トン作るにはAが3トンとBが1トン必要である.また,1日に使用できる薬品A, Bの量は,それぞれ18トン,13トンであり,XとYの1日の最大生産量は,4トンと5トンである.さらに,XとYの1トンあたりの価格は,30万円と50万円であるとし,1日にそれぞれxトンとyトン生産するものとする. (1) 上記の条件をxとyの連立不等式として表せ. (2) (1)の領域を図示せよ. (3) 1日に生産される製品XとYの合計金額をSとするとき,Sをxとyで表せ. (4) Sの最大値とそのときのXとYの生産量を求めよ. (2000年度立教大 社会学部)
(1)
3x+y≦13 0≦x≦4 0≦y≦5 (2) 右図の黄色で示した部分(内部および周上) (3) S=30x+50y (4) 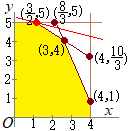 S=30x+50yの傾きは
S=30x+50yの傾きはこの傾きは, 与えられた領域の内部(および周上)でS=30x+50yの直線を描くと,赤丸 で示した このとき, Sの最大値は295(万円),そのとき |
|
【問題16】★☆☆
薬品A,Bがある.A,B各1gについて,P成分,Q成分,R成分の含有量と価格は,それぞれ下の表の通りである.1日当たりP成分を0.9mg以上,Q成分を1.2mg以上,R成分を8mg以上摂取する必要があるとする.これらを製品A,Bによってとるとき,1日あたりの費用を最小にするには,A,Bをそれぞれg,gずつとればよい.このときの費用は円である.
(2000年度日本大 薬学部)
薬品A,BをそれぞれA,Bgとるとすれば
A+2B≧1.2→傾き−0.5 5A+15B≧8 0≦A, B 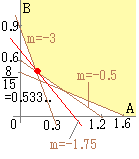 これを満たす領域は,右図の黄色で示した箇所の内部および周上
これを満たす領域は,右図の黄色で示した箇所の内部および周上1日あたりの費用をk円とすると k=35A+20B →傾き ここで,傾きは だから,領域内を通る直線k=35A+20Bでkが最小となるのは,赤丸で示した点 3A+B=0.9, A+2B=1.2の交点の座標はA=0.12(g), B=0.54(g)・・・(答) このとき,最小値はk=35A+20B=15(円)・・・(答) |
【問題17】★☆☆
[解説を読む]二種類の食品A,Bの100g当たりの栄養素含有率は下表の通りである.
(2000年度自治医大)
A,Bを各々a, b(g)とるとすると
0.05a+0.1b≧20 → 5a+10b≧2000・・・(2) 0≦a, b 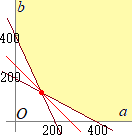 すなわち
すなわちa+2b≧400 0≦a, b 脂質がc(g)になるとすると c=0.03a+0.03b 右図の赤丸で示した点の座標は 最小値8(g)・・・(答) |