|
○ 中学校以来，グラフ，直線・曲線の方程式は，x と y の式で表わしている． 例 y=2x+3 例 x2+y2=9 など ○ このページでは，x 座標と x 座標を他の変数（媒介変数）の関数として表わした形を扱う． 例 x=t2 - 3 y=3t+1 |
■媒介変数表示のイメージ1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
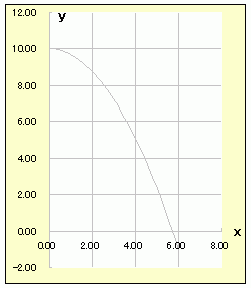
○ 物理の公式を用いると，高さ10(m)の屋上から水平方向に4(m/秒)の速さで投げ出された物体のt秒後のx座標とｙ座標は次の式で表わされる． x=4t y= - 4.9t2+10 
※t の値の上にマウスを置くと，対応する x , y の値とグラフ上の点の位置が示される．
○ この例では，時刻 t を媒介変数として x 座標と y 座標が決まり，それぞれの t の値について点が定まる． ○ 右の表を見ると「 x と y が対応している」ことが分かる． |
  |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
■ 媒介変数の消去とは 例 次の媒介変数表示において，t がすべての実数を変化するとき，点 (x , y) の通るグラフの方程式を x , y の関係式で表わすことを考える． x = 2t + 1 …(1) y = 3t - 1 …(2) (1)(2)は，次の式と同じ  x−12=t
すなわち，x−12= t = y+13
y+13=t書き直すと， x−12= y+13 ( = t )ここで，t が表舞台にいなくても x と y はつながっていることに気をつけると x−12= y+13すなわち，x , y の関係式は 3(x−1) = 2(y + 1) あるいは 3x−2y−5 = 0 …答 |
t は必要ならばいつでも登場できるが，当面舞台から隠れる． それでも x と y は，つながっている．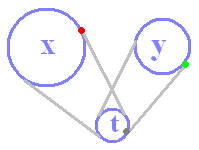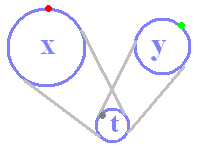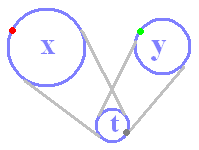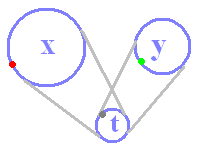 
 例 x=t2+1 , y=t−1 → t=?x などと考える必要はない． x=t2+1 , t=y+1 → x=(y+1)2+1 とすればよい． |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
［例題1］ ［媒介変数表示と軌跡］
［解答］t が実数値をとって変化するとき，次の式で表わされる点 P(x , y) の軌跡を求めよ． x=t+2 …(1) y=2t2−1 …(2) (1)より t=x−2 これを(2)に代入して t を消去すると y=2(x−2)2−1 …（答） ※ （参考） (1)より - ∞<t<∞ のとき - ∞<x<∞ となるから，答の放物線の全部が軌跡となる． |
［問題1］
(1)よりt が実数値をとって変化するとき，次の式で表わされる点 P(x , y) の軌跡を求めよ． x=t−1 …(1) y=2t+3 …(2) t=x+1 これを(2)に代入して t を消去すると y=2(x+1)+3=2x+5 …（答） |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
［例題2］ ［媒介変数消去と定義域］
t が実数値をとって変化するとき，次の式で表わされる点 P(x , y) の軌跡を求めよ． x=  √t+2 …(1)y=t …(2) t は根号の中にあるので正または0の値のみをとる．t≧0 …(*) 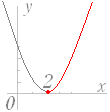 ［解答］
(1)より√t =x−2 …(3)ただし，t≧0 により x≧2 …(4) (3)を(2)に代入して t を消去すると y=(x−2)2 ただし x≧2 の部分 …（答） |
［問題2］
(1)よりt が実数値をとって変化するとき，次の式で表わされる点 P(x , y) の軌跡を求めよ． x=t2−2 …(1) y=3t2+4 …(2) t2=x+2 …(3) ただし，t2≧0 により x≧−2 …(4) (3)を(2)に代入して t を消去すると y=3(x+2)+4=3x+10 ただし x≧−2 の部分 …（答） |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
［例題3］ ［円の中心の軌跡］
a が実数値をとって変化するとき，次の式で表わされる円の中心の軌跡を求めよ． x2+y2−2ax+4ay+5a2−4=0
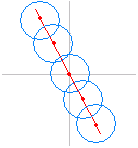 ［解答］(x−a)2+(y+2a)2=4 となるから 中心を P(x , y) とおくと x=a …(1) y=−2a …(2) (1)(2)よりa を消去すると y=−2x …（答） |
［問題3］
a が実数値をとって変化するとき，次の式で表わされる放物線の頂点の軌跡を求めよ． y=2x2+4ax+2a2+2a+1 y=2(x2+2ax)+2a2+2a+1 =2{ (x+a)2−a2 }+2a2+2a+1 =2(x+a)2+2a+1 頂点を P(x , y) とおくと x=−a …(1) y=2a+1 …(2) (1)(2)よりa を消去すると y=−2x+1 …（答） |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
■以下の内容は，教科書と比べると難しい，参考書では普通
［例題4］ ［媒介変数の実数条件］
m が実数値をとって変化するとき，次の式で表わされる点 P(x , y) の軌跡を求めよ． x= 1−m21+m2 …(1)y= 2m1+m2 …(2)
m について解いてから代入消去する必要はない．とにかく m を消去すればよい．十分性（除外点の有無）については後から検討すればよい．［解答］ 「なぜその変形を思い付くのか」という説明はいらない． (1)(2)より x2+y2=( 1−m21+m2)2+(2m1+m2)2= 1(1+m2)2(1−2m2+m4+4m2)= 1(1+m2)2(1+2m2+m4)=1よって，x2+y2=1 の円 （必要） (1)を m の２次方程式と見なしたとき， m の実数値が定まるための x の値の範囲を調べると (1+m2)x=1−m2 (x+1)m2+(x−1)=0 （ア） x≠−1 のとき D’=−(x+1)(x−1)≧0 より - 1≦x≦1 したがって - 1<x≦1 （イ） x=−1 のとき 0m2+(−2)=0 は実数解をもたない （ア）（イ）より - 1<x≦1 (2)を m の２次方程式と見なしたとき， m の実数値が定まるための y の値の範囲を調べると (1+m2)y=2m ym2−2m+y=0 （ア） y≠0 のとき D’=1−y2≧0 より - 1≦y≦1 したがって - 1≦y<0 , 0<y≦1 （イ） y=0 のとき 0m2−2m+0=0 は実数解 m=0 をもつ （ア）（イ）より - 1≦y≦1 以上より x=−1 すなわち，点 (−1 , 0) を除く 結局，x2+y2=1 の円のうち点 (−1 , 0) を除いたもの（答） |
※ x , y の取りうる値の範囲を調べるには，−∞<m<∞ のとき， x=−1+ 21+m2 および y=2m1+m2の取りうる値の範囲（関数の値域）を求めるのが確実な方法であるが，これは高校数学IIIの「分数関数の値域」で扱われる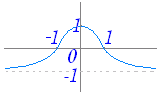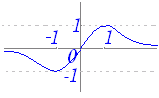．   グラフが書ければ - 1 <x≦1 ,−1≦y≦1 から (−1 , 0) が除外点であると分かるが，数学IIの答案では数IIIを習っていなくても解ける方法が必要なので，上記の話を使わずに左の答案のように方程式が実数解をもつための条件で求めるのが普通である．説明が分かりにくいのは「分数関数の値域」の話を避けたためである．（数学IIIまで習った人が数学IIの答案に使うのはよい） ○ ある (x , y) を通る ⇔ 対応する実数 m が存在する． この関係は，実数 m を先に決めなければならないと考える必要はなく， 「ある (x , y) 」を考えたときに「対応する実数 m が求まればよい．」 （「その m を代入すれば，その (x , y) が得られる」はずだから） ○ このようにして，
「通りうる (x , y) の値」 ⇔ 「 m の２次方程式と見なしたときに，実数解をもつ (x , y) の値」
によって， (x , y) の十分条件を検討すればよい． |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
［問題4］
m が実数値をとって変化するとき，次の式で表わされる点 P(x , y) の軌跡を求めよ． x= 2m1+m2 …(1)y= 21+m2 …(2)
|
(1)(2)より x2+y2=( 2mm2+1)2+(2m2+1)2= 4(m2+1)(m2+1)2= 4m2+1=2yよって，x2+(y−1)2=1 の円 （必要） (1)を m の２次方程式と見なしたとき， m の実数値が定まるための x の値の範囲を調べると (1+m2)x=2m xm2−2m+x=0 （ア） x≠0 のとき D’=1−x2≧0 より - 1≦x≦1 したがって - 1≦x<0 , 0<x≦1 （イ） x=0 のとき 0m2−2m+0=0 は実数解 m=0 をもつ （ア）（イ）より - 1≦x≦1 (2)を m の２次方程式と見なしたとき， m の実数値が定まるための y の値の範囲を調べると (1+m2)y=2 ym2+(y−2)=0 （ア） y≠0 のとき D’=−y(y−2)≧0 より 0≦y≦2 したがって 0<y≦2 （イ） y=0 のとき 0m2−2=0 は実数解をもたない （ア）（イ）より，点 (0 , 0) を除く 結局，x2+(y−1)2=1 の円のうち点 (0 , 0) を除いたもの（答） |
