■　軌跡の方程式１

○　点が動いたあとを「軌跡」という．
　右図１は，バッターが打った球が飛んで行った軌跡で，右図2は窓ガラスの表面をカタツムリが歩いた？軌跡のイメージ図である．

○　高校数学IIでは，「 xy 平面上で動点 P が与えられた条件を満たしながら動くとき， P の軌跡の方程式を求めよ．」という問題を扱う．

○　例えば，「２定点 A , B からの距離が等しい点の軌跡は，線分 AB の垂直二等分線になる」（中学校で習う二等辺三角形の性質 ⇒ 頂角の二等分線は底辺を垂直に二等分することから示される）が，この垂直二等分線の方程式は次の例題１のようにして求めることができる．
　なお，初歩的なことであるが， PA や PB の長さは一定ではなく，PA や PB の長さは変化するがそれらの長さは等しい：PA=PB という条件を満たしながら PA , PB の長さが変化することに注意．

［例題1］　［２定点から等距離にある点の軌跡］
　２定点 A( - 1 , 3) , B(3 , - 1) からの距離が等しい点の軌跡の方程式を求めよ．
［解答］
点 P の座標を (x , y) とおく．
　２点 AP 間の距離は AP=.√(x+1)2+(y−3)2√nnnnnnnnnnnni
　２点 BP 間の距離は BP=.√(x−3)2+(y+1)2√nnnnnnnnnnnni
AP=BPのとき
______.√(x+1)2+(y−3)2√nnnnnnnnnnnni=.√(x−3)2+(y+1)2√nnnnnnnnnnnni …(1)

両辺を２乗すると
______(x+1)2+(y−3)2=(x−3)2+(y+1)2
______x2+2x+1+y2−6y+9=x2−6x+9+y2+2y+1
______8x−8y=0
______y=x （必要条件）

逆に，y=x のとき，（この式を逆にたどっていくと）(1)が成り立つ．（十分条件）

ゆえに，求める軌跡の方程式は y=x …（答）
 図１
図２

■以下においてよく使う公式
【２点間の距離の公式】
　２点 A(x1 , y1 ) , B(x2 , y2 ) 間の距離は
______AB=.√(x2−x1)2+(y2−y1)2√nnnnnnnnnnnnnni

【要点】　軌跡の方程式の求め方
(I)　動点の座標を (x , y ) とおく．
「軌跡の方程式」とは，「動点の x 座標と y が満たす関係式」のことと考えればよい．これを求めるためには，必ず x 座標と y 座標がいる．
　軌跡の方程式を求めるためには，動点を P(x , y ) とおくことから始める．
(II) 与えられた条件を満たす x , y の関係式を作る．
「与えられた条件　⇒　関係式（図形）」で求まる式（図形）は，与えられた条件が成立するための「必要条件」になっている．
　すなわち，「ＡならばＢ」「Ａを変形したらＢになる」とき，「Ａのときは必ずＢになる」「Ａが成り立つときは必ずＢでなければならず，これ以外にはない」という関係にある．
　しかし，このようにして得られた関係式（図形）の全部が元の与えられた条件を満たすとは限らない（元よりも広い範囲になっていることがある）ので，その内のどの部分が与えられた条件を満たすか確かめなければならない．このために，次の(III)の手順で確かめる．
　得られた関係式のうちで元の与えられた条件を満たさない点は「除外点」と呼ばれる．(III)は「除外点」の検討になっている．
※　なお，この頁は簡単な問題だけを扱っているので，この頁の問題には除外点は含まれていない．たまたま，次の(III)のステップを忘れていても答が合っているように見えるのはそのためである．
(III) (II)で求めた関係式を満たす点が元の条件を満たすかどうか確かめる．
「関係式　⇒　与えられた条件」が成り立つかどうか調べる．「ＢならばＡ」が成り立つときＢはＡの「十分条件」と呼ばれる．十分条件が成り立つことを，十分性を満たすともいう．
［問題1］
　２定点 A(−2, 1) , B(3 , 0) から等距離にある点 P の軌跡を求めよ．
y=x−

採点する やり直す ヘルプ
［例題2］　［２定点からの距離の比が一定である点の軌跡］
　２定点 A(−2 , 0) , B(4 , 0) からの距離が 1 : 2 である点の軌跡を求めよ．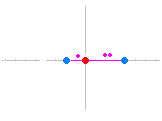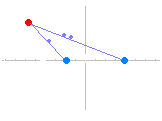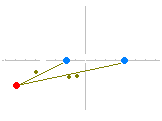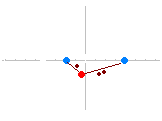
［解答］
点 P の座標を (x , y) とおく．
　２点 AP 間の距離は AP=.√(x+2)2+y2√nnnnnnnnni
　２点 BP 間の距離は BP=.√(x−4)2+y2√nnnnnnnnni
AP : BP=1 : 2 ならば
______.√(x+2)2+y2√nnnnnnnnni : .√(x−4)2+y2√nnnnnnnnni = 1 : 2 …(1)

内項の積・外項の積は等しいから
______2.√(x+2)2+y2√nnnnnnnnni = .√(x−4)2+y2√nnnnnnnnni
両辺を２乗すると
______4 { (x+2)2+y2 } = { (x−4)2+y2 }
______4 { x2+4x+4+y2 } = { x2−8x+16+y2 }
______4x2+16x+16+4y2 =x2−8x+16+y2
______3x2+24x+3y2=0
______x2+8x+y2=0
______(x+4)2+y2=16…(2) （必要条件）

逆に，(2) のとき，（この式を逆にたどっていくと）(1)が成り立つ．（十分条件）

ゆえに，求める軌跡の方程式は (x+4)2+y2=16
点 (−4 , 0) を中心とする半径 4 の円 …（答） 		○　一般に「２定点からの距離の比が一定（1:1を除く）であるような点の軌跡は円になる」ことが知られている．（1:1のときは２定点を結ぶ線分の垂直二等分線になる．）

○　このようにしてできる円を「アポロニウスの円」という．（アポロニウスはB.C.200年頃のギリシャの数学者 ）

○　左のアニメーションにおいて，２定点と動点とが一直線上に並ぶときを考えると，「アポロニウスの円は，２定点の内分点と外分点を直径の両端とする円になる．」ことが分かる．
　すなわち，「２定点Ａ，Ｂからの距離の比がｍ：ｎ（ただしｍ≠ｎ）である点の軌跡は，ＡＢをｍ：ｎに内分する点とｍ：ｎに外分する点をそれぞれ直径の両端とする円になる．」といえる．（教科書に書かれているとは限らないので，黙って使うことはできないが，結果を予測するのには役立つ．）
例　２定点 A(0 , 0) , B(4 , 0) からの距離が 3 : 1 である点の軌跡

AB を 3 : 1 に内分する点は C(3 , 0)
AB を 3 : 1 に外分する点は D(6 , 0)
CD が直径だから，中心 ( .92n , 0)，半径 .32n の円にな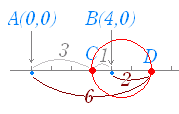る．
______(x−.92n )2+y2=( .32n)2
［問題2］
　２定点 A(−2 , 0) , B(3 , 0) に対して AP : BP=2 : 3 となる点 P の軌跡を求めよ．
中心の座標が ( , ) ，半径 の円

採点する やり直す ヘルプ
［例題3］　［２定点からの距離の２乗の差が一定である点の軌跡］
　２定点 A(−2 , 0) , B(2 , 0) に対して AP2−BP2=8 となる点 P の軌跡を求めよ．
［解答］
点 P の座標を (x , y) とおく．
______ { (x+2)2+y2 }−{ (x−2)2+y2 }=8
____________________________（２乗なので根号がはずれている．）
______ { x2+4x+4+y2 }−{ x2−4x+4+y2 }=8
______8x=8
______x=1

逆が成り立つのは明らか

ゆえに，求める軌跡の方程式は x=1 …（答） 		※　記号 AP は線分 AP の長さを表わし，AP2 は AP×AP を表わす．
　例えば AP=3 ならば AP2=9 となる．
　一般の文字式 ab2 などとは異なり， P だけを２乗している訳ではない．

（参考）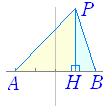
左の問題を，中学校で習う三平方の定理で考えると次のように解ける．
______AP2=AH2+PH2
_- ) BP2=BH2+PH2

______AP2−BP2=AH2−BH2=8
ここで AH+HB=4 だから AH−HB=2
となる点 H に立てた垂線 HP 上に P があればよい．
［問題3］
　２定点 A(−2 , 0) , B(2 , 0) に対して AP2+BP2=16 となる点 P の軌跡を求めよ．
x2+y2=

採点する やり直す ヘルプ
［類題1］
　２定点 A(1 , 2) , B(3 ,−4) から等距離にある点 P の軌跡を求めよ．
x−y−=0

採点する やり直す ヘルプ
［類題2］
　２定点 A(−2 , 0) , B(6 , 0) からの距離の比が 1 : 3 である点の軌跡を求めよ．
中心の座標が ( , ) ，半径 の円

採点する やり直す ヘルプ
［類題3］
　２定点 A(0 , 0) , B(6 , 0) に対して AP2−BP2=24 となる点 P の軌跡を求めよ．
x=

採点する やり直す ヘルプ
○===メニューに戻る
■［個別の頁からの質問に対する回答］[軌跡の方程式１について／17.6.19］
半世紀ぶりの数学の学び直し、脳内の霧が晴れていくような気持がしています。本当に有難いサイトです。ありがとうございます。
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[軌跡の方程式１について／17.6.10］
例題1の解答で２点 AP 間の距離は AP=√(x+1)2+(y－3)2 とありましだか、それはどうしてですか？？詳しくお願いします！！よろしくお願いします！
＝＞［作者］：連絡ありがとう．回答の文章を考えるときに，いつも思うのは，この人は何歳ぐらいの人で，この分野の内容をどれくらいやった人なのだろうかが不明の場合に，どこまで答えるのかということです．もし，高校生になっていない人が，たまたま検索でヒットした頁に質問しているのなら，それなりに事前学習をしてもらわないと言えないこともあります．
その頁の右半分に書いてありますように，２点間の距離はです．
したがって，２点間の距離はです．
これが「なぜ？」ということでしたら，中学校３年のこの教材を初めに読んでいただく必要があります．
■［個別の頁からの質問に対する回答］[軌跡の方程式について／17.1.5］
とても分かりやすかった
＝＞［作者］：連絡ありがとう．

■このサイト内のGoogle検索■

△このページの先頭に戻る△
【 アンケート送信 】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．
○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）


質問に対する回答の中学版はこの頁，高校版はこの頁にあります