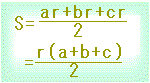内接円の半径

→ 携帯版は別頁

このページのマイナーチェンジありカバー版ページ
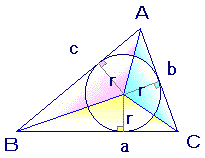
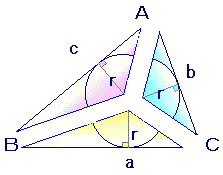
（グーグルブロガー版）は，こちら⇒

== 内接円の半径 == 《解説》
■三角形の内接円の半径の大きさは，面積と関係付けることができます.

　三角形の内接円の半径をｒとおく.
　三角形を右図のように3つに分けると，

と表せることが分かります.
　さらに，(ａ＋ｂ＋ｃ)/2＝ｓとおくと

Ｓ＝ｒｓ　となります.

■三角形の面積は，いろんな求め方があります.そこで，ヘロンの公式などを用いて三角形の面積を求めておくと，内接円の半径が求まります.

【ヘロンの公式】
三辺の長さがa , b , cである三角形の面積Sを求めるには

まず、s= を求めておき

次に、S= …(1)
とします。

(1)はS= …(2)

と書くこともできますが、教科書では通常(1)の形で書かれています。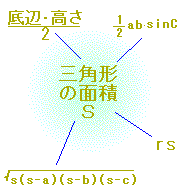

ヘロンの公式で求めた面積は、他の方法で求めた面積と等しいはずだということを使います。 ■例
　三角形の３辺の長さが，それぞれ13,14,15のとき，内接円の半径を求めなさい.
（答案）
　ｓ＝（13+14+15）／２＝21

　ヘロンの公式により、Ｓ＝
　他方，Ｓ＝21r　
　ゆえに，ｒ＝４・・・(答)

《問題1》

　三角形の３辺の長さが次のように与えられているとき，この三角形の内接円の半径を求めなさい.

（1）３，４，５
（2）９，１０，１７
（3）１１，１３，２０
（4）１５，２６，３７

《問題２》

　次の三角形の内接円の半径を求めなさい.

（1）ａ＝８，ｂ＝３，Ｃ＝60°
（2） b=15，ｃ＝7，A=60°
（3）ｃ＝３，ａ＝５，Ｂ＝120°
（4）ａ＝５，ｂ＝16，Ｃ＝120°

《問題３》

　三角形ＡＢＣにおいて(ＣＡ＋ＡＢ)：(ＢＣ＋ＣＡ)：(ＡＢ＋ＢＣ)＝５：６：７である.
(1)　sinＡを求めよ.
(2)　三角形ＡＢＣの内接円と外接円の半径の比を求めよ.

（昭和女子大入試問題からの引用）

(1)
　の形で求めると， 　ア＝，イ＝

(2)
　　：　

　

(1) (b+c):(a+b):(c+a)=5:6:7からa:b:cが求められます。（比率のみ）

(b+c):(a+b):(c+a)=5:6:7よりb+c=5k , a+b=6k , c+a=7k
この連立方程式を解くとa=4k , b=2k , c=3k

a:b:cが分かれば、余弦定理の変形によりcosAが求められ、これによりsinAが求められます。

余弦定理の変形：cosA= = − ⇒ sinA(>0)===

(2) 外接円の半径Rは正弦定理=2Rによって求められます。

=2R　⇒　R=k

内接円の半径はS=rsによって求められます。ここで面積は、ヘロンの公式によって求めます。

a=4k , b=2k , c=3kからs==

S= = k2 ⇒ S=rsよりr= k

以上により、r:R= k : k=5:16

（参考）
　△ABCについて
内接円の半径をr，外接円の半径をR，面積をS，３辺の長さの和の半分を $s=\frac{a+ b+ c}{2}$ とするとき，これらについて成り立つ関係（まとめ）

(1) ２辺とその間の角で面積を表す
$S=\frac{1}{2}bc\sin A=\frac{1}{2}ca\sin B=\frac{1}{2}ab\sin C$
(2)　３辺と外接円の半径で面積を表す

$S=\frac{abc}{4R}$

正弦定理 $\frac{a}{\sin A}=2R$ から
$\sin A=\frac{a}{2R}$
これを(1)に代入すると
$S=\frac{1}{2}bc\cdot\frac{a}{2R}=\frac{abc}{4R}$

(3)　３辺の長さの和と内接円の半径で面積を表す

$S=\frac{1}{2}(a+ b+ c)r=rs$

このページの先頭の解説図

...メニューに戻る