●1の解説:
●2の解説:
●3の解説:
|
このページのマイナーチェンジありカバー版ページ(2023.02.09更新)
(グーグルブロガー版)は,こちら⇒ 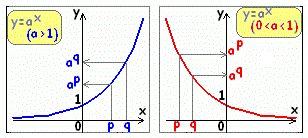
22x-4=22-x → 2x-4=2-x これで指数は外れましたので、あとは単なる1次方程式です。 3x=6 より x=2・・・答 ●2の例
●3の例
|
●1の解説:
●2の解説:
●3の解説:
|
このページのマイナーチェンジありカバー版ページ(2023.02.09更新)
(グーグルブロガー版)は,こちら⇒ 
22x-4=22-x → 2x-4=2-x これで指数は外れましたので、あとは単なる1次方程式です。 3x=6 より x=2・・・答 ●2の例
●3の例
|
|
■問題・・・次の方程式を解きなさい。 1 |
[ヒント]
(32)3x=(33)x-1
==> 36x=33x-3 ==> 6x=3x-3 |
| 2 | [ヒント]
(21/2)x=22
==> 2x/2=22 ==> x/2=2 |
| 3 | [ヒント]
(3-1)1-x=(32)x
==> 3x-1=32x ==>x-1=2x |
| 4 | [ヒント]
2x-3=(2-2)x
==> 2x-3=2-2x ==> x-3=-2x |
| 5
--※対数を習ってからする問題
|
[ヒント]
対数の定義
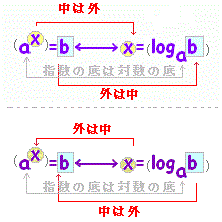
|
|
6--※対数を習ってからする問題
|
[ヒント]
対数の定義
 |
| 7
|
[ヒント]
3x=t (t>0) とおく ==> t2-4t+3=0
==> (t-1)(t-3)=0 ==> t=1,3 ==> 3x=1,3 |
| 8 | [ヒント]
2x=t (t>0) とおく ==> t2-2t-8=0
==> (t-4)(t+2)=0
t>0 を満たすものからxを求める。 |
|
■[個別の頁からの質問に対する回答][指数方程式について/16.10.22]
最後の問題8番の、2の2x乗-2のx+1乗-8についての質問です。ヒントでは2のx乗をtとすると、tの2乗-2t-8になるとあります。しかし、tの2乗+4t-8になるような気がして、そこで行き詰ってしまったのですが、いかがでしょうか。
=>[作者]:連絡ありがとう.あなたの場合は,指数法則が十分身に付いていないという弱点があるようですので,この頁で復習するとよいでしょう.なお,指数法則や対数の計算規則は,1つの問題の中で何回も多重的に登場しますので,(水や空気に親しむように)反復練習が必要です. 元の問題:
amn=(am)nだから2x=tとおくと22x=(2x)2=t2
−2x+1は(−2)22x→4tにはなりません
次に am+n=amanだから2x+1=2x21すなわち2x+1=2t になります. |