|
5. 平行な2直線間の距離
【例題5】
平行な2直線  \( \displaystyle x-1=\frac{y-3}{2}=\frac{z+ 1}{-2},\hspace{2px}x=\frac{y}{2}=\frac{z}{-2} \) \( \displaystyle x-1=\frac{y-3}{2}=\frac{z+ 1}{-2},\hspace{2px}x=\frac{y}{2}=\frac{z}{-2} \)間の距離を求めてください.
 (解答)
(解答)
いずれか一方の直線上の点,例えば直線
 \( \displaystyle x-1=\frac{y-3}{2}=\frac{z+ 1}{-2} \)上の点 \( \displaystyle x-1=\frac{y-3}{2}=\frac{z+ 1}{-2} \)上の点
) \( \displaystyle \rm{P_1}(1,\hspace{2px}3,\hspace{2px}-1) \)と他方の直線 \( \displaystyle \rm{P_1}(1,\hspace{2px}3,\hspace{2px}-1) \)と他方の直線
 \( \displaystyle x=\frac{y}{2}=\frac{z}{-2} \)の間の距離を測ればよい. \( \displaystyle x=\frac{y}{2}=\frac{z}{-2} \)の間の距離を測ればよい.
) \( \displaystyle \overrightarrow{\rm{P_0P_1}}=(1,\hspace{2px}3,\hspace{2px}-1) \), \( \displaystyle \overrightarrow{\rm{P_0P_1}}=(1,\hspace{2px}3,\hspace{2px}-1) \),
) \( \displaystyle \vec{u}=(1,\hspace{2px}2,\hspace{2px}-2) \)だから \( \displaystyle \vec{u}=(1,\hspace{2px}2,\hspace{2px}-2) \)だから
) \( \displaystyle \overrightarrow{\rm{P_0P_1}}\times\vec{u}=\begin{vmatrix}\vec{e_1}&\vec{e_2}&\vec{e_3}\\1& 3& -1\\ 1& 2& -2\end{vmatrix}=(-4,\hspace{2px}1,\hspace{2px}-1) \) \( \displaystyle \overrightarrow{\rm{P_0P_1}}\times\vec{u}=\begin{vmatrix}\vec{e_1}&\vec{e_2}&\vec{e_3}\\1& 3& -1\\ 1& 2& -2\end{vmatrix}=(-4,\hspace{2px}1,\hspace{2px}-1) \)
 \( \displaystyle h=\frac{\sqrt{16+ 1+ 1}}{\sqrt{1+ 4+ 4}}=\frac{\sqrt{18}}{\sqrt{9}}=\sqrt{2} \)
…(答) \( \displaystyle h=\frac{\sqrt{16+ 1+ 1}}{\sqrt{1+ 4+ 4}}=\frac{\sqrt{18}}{\sqrt{9}}=\sqrt{2} \)
…(答)
【問題5.1】
平行な2直線  \( \displaystyle \frac{x-1}{2}=y-2=z-3,\hspace{2px}\frac{x-1}{2}=y+ 1=z \) \( \displaystyle \frac{x-1}{2}=y-2=z-3,\hspace{2px}\frac{x-1}{2}=y+ 1=z \)間の距離を求めてください.
解答を見る解答を隠す
(解答)
一方の直線  \( \displaystyle \frac{x-1}{2}=y-2=z-3 \) \( \displaystyle \frac{x-1}{2}=y-2=z-3 \)上の点
) \( \displaystyle \rm{P_1}(1,\hspace{2px}2,\hspace{2px}3) \) \( \displaystyle \rm{P_1}(1,\hspace{2px}2,\hspace{2px}3) \)と他方の直線
 \( \displaystyle \frac{x-1}{2}=y%2B 1=z \) \( \displaystyle \frac{x-1}{2}=y%2B 1=z \)の間の距離を測ればよい.
点Pの座標を

 \( \displaystyle x=2t+ 1 \) \( \displaystyle x=2t+ 1 \)
 \( \displaystyle y=t-1 \) \( \displaystyle y=t-1 \)
 \( \displaystyle z=t \) \( \displaystyle z=t \)
とおくと,
^2%2B(t-3)^2%2B(t-3)^2) \( \displaystyle |P_1P|^2=(2t)^2+(t-3)^2+(t-3)^2 \) \( \displaystyle |P_1P|^2=(2t)^2+(t-3)^2+(t-3)^2 \)
^2%2B 12) \( \displaystyle |P_1P|^2=6t^2-12t+ 18=6(t-1)^2+ 12 \) \( \displaystyle |P_1P|^2=6t^2-12t+ 18=6(t-1)^2+ 12 \)
これはt=1のとき最小値をとる.
最小値は  \( \displaystyle |P_1P|=\sqrt{12}=2\sqrt{3} \) \( \displaystyle |P_1P|=\sqrt{12}=2\sqrt{3} \)…(答)
(別解)
一方の直線  \( \displaystyle \frac{x-1}{2}=y-2=z-3 \) \( \displaystyle \frac{x-1}{2}=y-2=z-3 \)上の点
) \( \displaystyle \rm{P_1}(1,\hspace{2px}2,\hspace{2px}3) \) \( \displaystyle \rm{P_1}(1,\hspace{2px}2,\hspace{2px}3) \)から他方の直線
 \( \displaystyle \frac{x-1}{2}=y+ 1=z \) \( \displaystyle \frac{x-1}{2}=y+ 1=z \)に垂線を引けばよい.
点Pの座標を

 \( \displaystyle x=2t+1 \) \( \displaystyle x=2t+1 \)
 \( \displaystyle y=t-1 \) \( \displaystyle y=t-1 \)
 \( \displaystyle z=t \) \( \displaystyle z=t \)
とおくと,
) \( \displaystyle \overrightarrow{\rm{P_1P}}=(2t,\hspace{2px}t-3,\hspace{2px}t-3) \) \( \displaystyle \overrightarrow{\rm{P_1P}}=(2t,\hspace{2px}t-3,\hspace{2px}t-3) \)が
) \( \displaystyle \vec{u}=(2,\hspace{2px}1,\hspace{2px}1) \) \( \displaystyle \vec{u}=(2,\hspace{2px}1,\hspace{2px}1) \)と垂直になればよいから
%2B (t-3)%2B (t-3)=0) \( \displaystyle 2(2t)+ (t-3)+ (t-3)=0 \) \( \displaystyle 2(2t)+ (t-3)+ (t-3)=0 \)
 \( \displaystyle 6t-6=0 \) \( \displaystyle 6t-6=0 \)
 \( \displaystyle t=1 \) \( \displaystyle t=1 \)
このとき
) \( \displaystyle \rm{P}(3,\hspace{2px}0,\hspace{2px}1) \) \( \displaystyle \rm{P}(3,\hspace{2px}0,\hspace{2px}1) \)
^2%2B(0-2)^2%2B(1-3)^2}=\sqrt{12}=2\sqrt{3}&chs=350x30) \( \displaystyle |\rm{P_1P}|=\sqrt{(3-1)^2+(0-2)^2+(1-3)^2}=\sqrt{12}=2\sqrt{3} \) \( \displaystyle |\rm{P_1P}|=\sqrt{(3-1)^2+(0-2)^2+(1-3)^2}=\sqrt{12}=2\sqrt{3} \)…(答)
|
【問題5.2】
平行な2直線  \( \displaystyle \frac{x-1}{2}=\frac{y-2}{3},\hspace{2px}z=3 \) \( \displaystyle \frac{x-1}{2}=\frac{y-2}{3},\hspace{2px}z=3 \)と
 \( \displaystyle \frac{x-3}{2}=\frac{y-5}{3},\hspace{2px}z=2 \) \( \displaystyle \frac{x-3}{2}=\frac{y-5}{3},\hspace{2px}z=2 \)間の距離を求めてください.
解答を見る解答を隠す
(別解2)
直線  \( \displaystyle \frac{x-1}{2}=\frac{y-2}{3},\hspace{2px}z=3 \) \( \displaystyle \frac{x-1}{2}=\frac{y-2}{3},\hspace{2px}z=3 \)上の1点P 0(1, 2, 3)と
直線  \( \displaystyle \frac{x-3}{2}=\frac{y-5}{3},\hspace{2px}z=2 \) \( \displaystyle \frac{x-3}{2}=\frac{y-5}{3},\hspace{2px}z=2 \)上の1点P 1(3, 5, 2)に対して例題5と同様に,
) \( \displaystyle \overrightarrow{\rm{P_0P_1}}=(2,\hspace{2px}3,\hspace{2px}-1) \) \( \displaystyle \overrightarrow{\rm{P_0P_1}}=(2,\hspace{2px}3,\hspace{2px}-1) \)と方向ベクトル
) \( \displaystyle \vec{u}=(3,\hspace{2px}-2,\hspace{2px}0) \) \( \displaystyle \vec{u}=(3,\hspace{2px}-2,\hspace{2px}0) \)の外積を用いて計算すると
) \( \displaystyle \overrightarrow{\rm{P_0P_1}}\times\vec{u}=\begin{vmatrix}\vec{e_1}&\vec{e_2}&\vec{e_3}\\2& 3& -1\\2& 3& 0\end{vmatrix}=(3,\hspace{2px}-2,\hspace{2px}0) \) \( \displaystyle \overrightarrow{\rm{P_0P_1}}\times\vec{u}=\begin{vmatrix}\vec{e_1}&\vec{e_2}&\vec{e_3}\\2& 3& -1\\2& 3& 0\end{vmatrix}=(3,\hspace{2px}-2,\hspace{2px}0) \)
 \( \displaystyle h=\frac{|\overrightarrow{\rm{P_0P_1}}\times\vec{u}|}{|\vec{u}|}=\frac{\sqrt{13}}{\sqrt{13}}=1 \) \( \displaystyle h=\frac{|\overrightarrow{\rm{P_0P_1}}\times\vec{u}|}{|\vec{u}|}=\frac{\sqrt{13}}{\sqrt{13}}=1 \)
(解答)
直線  \( \displaystyle \frac{x-1}{2}=\frac{y-2}{3},\hspace{2px}z=3 \) \( \displaystyle \frac{x-1}{2}=\frac{y-2}{3},\hspace{2px}z=3 \)上の1点P 0(1, 2, 3)と
直線  \( \displaystyle \frac{x-3}{2}=\frac{y-5}{3},\hspace{2px}z=2 \) \( \displaystyle \frac{x-3}{2}=\frac{y-5}{3},\hspace{2px}z=2 \)上の点P(x, y, z)

 \( \displaystyle x=2t+ 3 \) \( \displaystyle x=2t+ 3 \)
 \( \displaystyle y=3t+ 5 \) \( \displaystyle y=3t+ 5 \)
 \( \displaystyle z=2 \) \( \displaystyle z=2 \)
の間の距離は
^2%2B(3t%2B 3)^2%2B 1^2) \( \displaystyle \rm{P_0P}^2=(2t+ 2)^2+(3t+ 3)^2+ 1^2 \) \( \displaystyle \rm{P_0P}^2=(2t+ 2)^2+(3t+ 3)^2+ 1^2 \)
 \( \displaystyle =4t^2+ 8t+ 4+ 9t^2+ 18t+ 9+ 1 \) \( \displaystyle =4t^2+ 8t+ 4+ 9t^2+ 18t+ 9+ 1 \)
^2%2B 1) \( \displaystyle =13t^2+ 26t+ 14=13(t+ 1)^2+ 1 \) \( \displaystyle =13t^2+ 26t+ 14=13(t+ 1)^2+ 1 \)
はt=−1のとき最小値  \( \displaystyle P_0P=1 \) \( \displaystyle P_0P=1 \)となる.これが2直線間の距離に等しい.
【問題5.3】
平行な2直線  \( \displaystyle \frac{x-8}{4}=\frac{y+ 1}{3}=\frac{z-4}{2} \) \( \displaystyle \frac{x-8}{4}=\frac{y+ 1}{3}=\frac{z-4}{2} \)と
 \( \displaystyle \frac{x-1}{4}=\frac{y}{3}=\frac{z-2}{2} \) \( \displaystyle \frac{x-1}{4}=\frac{y}{3}=\frac{z-2}{2} \)と間の距離を求めてください.
解答を見る解答を隠す
(別解2)
直線  \( \displaystyle \frac{x-8}{4}=\frac{y+ 1}{3}=\frac{z-4}{2} \) \( \displaystyle \frac{x-8}{4}=\frac{y+ 1}{3}=\frac{z-4}{2} \)上の1点P 0(8, −1, 4)と
直線  \( \displaystyle \frac{x-1}{4}=\frac{y}{3}=\frac{z-2}{2} \) \( \displaystyle \frac{x-1}{4}=\frac{y}{3}=\frac{z-2}{2} \)上の1点P 1(1, 0, 2)に対して例題5と同様に,
) \( \displaystyle \overrightarrow{\rm{P_0P_1}}=(-7,\hspace{2px}1,\hspace{2px}-2) \) \( \displaystyle \overrightarrow{\rm{P_0P_1}}=(-7,\hspace{2px}1,\hspace{2px}-2) \)と方向ベクトル
) \( \displaystyle \vec{u}=(4,\hspace{2px}3,\hspace{2px}2) \) \( \displaystyle \vec{u}=(4,\hspace{2px}3,\hspace{2px}2) \)の外積を用いて計算すると
) \( \displaystyle \overrightarrow{\rm{P_0P_1}}\times\vec{u}=\begin{vmatrix}\vec{e_1}&\vec{e_2}&\vec{e_3}\\-7& 1& -2\\4& 3& 2\end{vmatrix}=(8,\hspace{2px}6,\hspace{2px}-25) \) \( \displaystyle \overrightarrow{\rm{P_0P_1}}\times\vec{u}=\begin{vmatrix}\vec{e_1}&\vec{e_2}&\vec{e_3}\\-7& 1& -2\\4& 3& 2\end{vmatrix}=(8,\hspace{2px}6,\hspace{2px}-25) \)
 \( \displaystyle h=\frac{|\overrightarrow{\rm{P_0P_1}}\times\vec{u}|}{|\vec{u}|}=\frac{\sqrt{725}}{\sqrt{29}}=5 \) \( \displaystyle h=\frac{|\overrightarrow{\rm{P_0P_1}}\times\vec{u}|}{|\vec{u}|}=\frac{\sqrt{725}}{\sqrt{29}}=5 \)
(解答)
直線  \( \displaystyle \frac{x-8}{4}=\frac{y+ 1}{3}=\frac{z-4}{2} \) \( \displaystyle \frac{x-8}{4}=\frac{y+ 1}{3}=\frac{z-4}{2} \)上の1点P 0(8, −1, 4)と
直線  \( \displaystyle \frac{x-1}{4}=\frac{y}{3}=\frac{z-2}{2} \) \( \displaystyle \frac{x-1}{4}=\frac{y}{3}=\frac{z-2}{2} \)上の点P(x, y, z)

 \( \displaystyle x=4t+ 1 \) \( \displaystyle x=4t+ 1 \)
 \( \displaystyle y=3t \) \( \displaystyle y=3t \)
 \( \displaystyle z=2t+2 \) \( \displaystyle z=2t+2 \)
の間の距離は
^2%2B(3t%2B 1)^2%2B (2t-2)^2) \( \displaystyle \rm{P_0P}^2=(4t-7)^2+(3t+1)^2+ (2t-2)^2 \) \( \displaystyle \rm{P_0P}^2=(4t-7)^2+(3t+1)^2+ (2t-2)^2 \)
 \( \displaystyle =16t^2-56t+ 49+ 9t^2+ 6t+ 1+ 4t^2-8t+ 4 \) \( \displaystyle =16t^2-56t+ 49+ 9t^2+ 6t+ 1+ 4t^2-8t+ 4 \)
^2%2B 25) \( \displaystyle =29t^2-58t+ 54=29(t-1)^2+ 25 \) \( \displaystyle =29t^2-58t+ 54=29(t-1)^2+ 25 \)
はt=1のとき最小値  \( \displaystyle \rm{P_0P}=5 \) \( \displaystyle \rm{P_0P}=5 \)となる.これが2直線間の距離に等しい.
|
 「点P1を通り,方向ベクトル
「点P1を通り,方向ベクトル
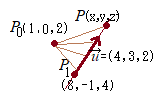 (解答)
(解答)
 (別解1)
(別解1)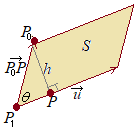 (別解2)
(別解2) (解答)
(解答) 点
点 右図のように直線と
右図のように直線と 2直線のなす角は,2直線の方向ベクトルのなす角で定義される.ねじれの位置にある場合でも2直線のなす角を考えます.
2直線のなす角は,2直線の方向ベクトルのなす角で定義される.ねじれの位置にある場合でも2直線のなす角を考えます.