|
گüŒ`‘مگ”.‰‰ڈKƒmپ[ƒgپiƒAƒ“ƒTپ[ƒuƒbƒNپj
پ@‚±‚جƒyپ[ƒW‚ة‚حپCŒِ•\‚³‚ꂽ’کچى•¨پi’کچىŒ –@‘و32ڈًپj‚جˆّ—p‚ھٹـ‚ـ‚ê‚ؤ‚¢‚ـ‚·پD
** ‚RژںŒ³‹َٹش‚ة‚¨‚¯‚é’¼گü‚ج•û’ِژ® **پ@‰ً‚«•ûپC“r’†Œo‰ك‚ب‚ا‚ة‚حپCŒ´’کچى•¨‚ة‚ح‚ب‚¢(‚±‚جƒyپ[ƒW‚جٹا—گl‚ج)‰ًژك‚ھٹـ‚ـ‚ê‚ؤ‚¢‚ـ‚·پD
پy—v“_پz
3ژںŒ³‹َٹش‚ة‚¨‚¯‚é’¼گü‚جƒxƒNƒgƒ‹•û’ِژ®پCƒpƒ‰ƒپپ[ƒ^•\ژ¦(”}‰î•دگ”•\ژ¦پCڈ••دگ”•\ژ¦)پCxyz•û’ِژ®
پZ3ژںŒ³‹َٹش‚ة‚¨‚¢‚ؤپC“_پZ‚±‚ê‚ًگ¬•ھ‚إ•\‚·‚ئ پZٹeگ¬•ھ‚ة•ھ‚¯‚é‚ئ پZƒpƒ‰ƒپپ[ƒ^‚ًڈء‹ژ‚µ‚ؤ 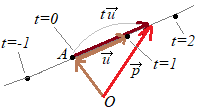 پi‰ًگàپj
پi‰ًگàپj(1)← پ@—ل‚¦‚خپC (1)‚ًگ¬•ھ‚إڈ‘‚¢‚½(2)‚ـ‚½‚ح(3)‚ً(3ژںŒ³‹َٹش‚ة‚¨‚¯‚é)’¼گü‚جƒpƒ‰ƒپپ[ƒ^•\ژ¦(”}‰î•دگ”•\ژ¦پCڈ••دگ”•\ژ¦)پCƒpƒ‰ƒپپ[ƒ^•û’ِژ®‚ئ‚¢‚¤پD (4)← (3)‚ج•û’ِژ®‚ً ‚حپC ‚àچ‚چZگ”ٹw‚إˆµ‚¤پD |
پ@‚½‚¾‚µپC(4)‚ح
پ@‚½‚ئ‚¦‚خپC“_ ‚ئ‚ب‚é‚ھپC(3)‚إچl‚¦‚ؤ‚ف‚é‚ئ•ھ‚©‚é‚و‚¤‚ة ‚ً•\‚µ‚ؤ‚¢‚éپD•ھ•ê‚ھ‚O‚ة‚ب‚ç‚ب‚¢ڈ‘‚«•û‚إ‚ح ‚ً•\‚·پD پ@‚ـ‚½پC‚½‚ئ‚¦‚خپC“_ ‚ئ‚ب‚é‚ھپC(3)‚إچl‚¦‚ؤ‚ف‚é‚ئ•ھ‚©‚é‚و‚¤‚ة ‚ً•\‚µ‚ؤ‚¢‚éپD•ھ•ê‚ھ‚O‚ة‚ب‚ç‚ب‚¢ڈ‘‚«•û‚إ‚ح ‚ً•\‚·پD‚ب‚¨پCگ§Œہ‚ھ‚ب‚¢‚±‚ئ‚ح•û’ِژ®‚ئ‚µ‚ؤڈ‘‚©‚ب‚‚ؤ‚و‚¢‚©‚çپC‚±‚ê‚حژں‚جŒ`‚ةڈ‘‚¯‚éپD پ@
پy—v“_پz
پZ3ژںŒ³‹َٹش‚ة‚¨‚¢‚ؤپC‚Q“_ (2)پ`(4)‚à“¯—l |
|
ژں‚ج“_‚ً’ت‚é’¼گü‚جƒpƒ‰ƒپپ[ƒ^•û’ِژ®‚ً‹پ‚ك‚وپD
1.(1, 1, −1)‚ئ(−2, 1, 3)
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.15
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.037
1.A(1, 1, −1),B(−2, 1, 3)‚ئ‚¨‚‚ئپC“_A‚ً’ت‚èپC•ûŒüƒxƒNƒgƒ‹
‚ة•½چs‚ب’¼گü‚¾‚©‚ç گ¬•ھ‚ة•ھ‚¯‚ؤپCژں‚جŒ`‚إڈ‘‚¢‚ؤ‚à‚و‚¢پD B(−2, 1, 3)‚ً’ت‚èپC•ûŒüƒxƒNƒgƒ‹ ‚ة•½چs‚ب’¼گü‚ئچl‚¦‚é‚ئ گ¬•ھ‚ة•ھ‚¯‚ؤپCژں‚جŒ`‚إڈ‘‚¢‚ؤ‚à‚و‚¢پD پiژQچl1پj‚±‚ج’¼گü‚ج•û’ِژ®‚ًپCxyz‚ج•û’ِژ®‚إڈ‘‚¯‚خ پiژQچl2پjکa–َˆّ—pŒ³‚إ‚حپC‚RژںŒ³‹َٹش‚ج“_‚جچہ•W‚àƒxƒNƒgƒ‹‚àپC‚¢‚¸‚ê‚à ‚ئ‚ب‚ء‚ؤ‚¢‚éپD پ@‚±‚ê‚àگ³‚µ‚¢‚ج‚¾‚ھپC پ@‚ب‚¨پC(“ڑ3)‚جƒpƒ‰ƒپپ[ƒ^‚ً پi ‚ئ‚ب‚ء‚ؤپCŒ©‚©‚¯‚ھˆظ‚ب‚é‚ھپC•\‚µ‚ؤ‚¢‚é‚à‚ج‚ح“¯‚¶ |
ژں‚ج“_‚ً’ت‚é’¼گü‚جƒpƒ‰ƒپپ[ƒ^•û’ِژ®‚ً‹پ‚ك‚وپD
2.(−1, 5, 2)‚ئ(3, −4, 1)
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.15
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.037
1.A(−1, 5, 2),B(3, −4, 1)‚ئ‚¨‚‚ئپC“_A‚ً’ت‚èپC•ûŒüƒxƒNƒgƒ‹
‚ة•½چs‚ب’¼گü‚¾‚©‚ç گ¬•ھ‚ة•ھ‚¯‚ؤپCژں‚جŒ`‚إڈ‘‚¢‚ؤ‚à‚و‚¢پD پiژQچlپjکa–َˆّ—pŒ³‚إ‚حپC‰ً“ڑ‚ح |
|
** ‚QژںŒ³•½–ت‚ة‚¨‚¯‚é’¼گü‚ج•û’ِژ® **
پy—v“_پz
پi‰ًگàپj•½–تڈم‚إ‚P“_‚ً’ت‚èپC—^‚¦‚ç‚ꂽƒxƒNƒgƒ‹‚ةگ‚’¼‚ب’¼گü‚ج•û’ِژ®
پZ•½–ت‚ة‚¨‚¢‚ؤپC“_پZ•½–ت‚ة‚¨‚¢‚ؤپC“_  “_
“_‚ھگ¬‚è—§‚آپD‚µ‚½‚ھ‚ء‚ؤ ‚ھگ¬‚è—§‚آپD‚ـ‚½پC‹t‚ة(2)‚ھگ¬‚è—§‚ؤ‚خپC“_ |
ژں‚ج‚`‚ئ‚o‚ة‘خ‚µ‚ؤپA‚o‚ً’ت‚è‚`‚ةگ‚’¼‚بپi‚Q-‹َٹش‚جپj’¼گü‚ج•û’ِژ®‚ً‹پ‚ك‚وپD
پ¦1 ڈم‹L‚ج‹³‰بڈ‘‚إ‚حپC“_‚جچہ•W‚àƒxƒNƒgƒ‹‚àپC‚¢‚¸‚ê‚à3.A=(1, −1)پCP=(−5, 3)
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.15
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.037 پ¦2 ڈم‹L‚ج‹³‰بڈ‘‚إ‚حپC‚QژںŒ³‚ج•½–ت R2‚ج‚±‚ئ‚ً(‚Q-‹َٹشپjپC‚RژںŒ³‚ج‹َٹش R3‚ج‚±‚ئ‚ًپi‚R-‹َٹشپj‚ئڈ‘‚¢‚ؤ‚¢‚éپD
ژں‚ج‚`‚ئ‚o‚ة‘خ‚µ‚ؤپA‚o‚ً’ت‚è‚`‚ةگ‚’¼‚بپi‚Q-‹َٹش‚جپj’¼گü‚ج•û’ِژ®‚ً‹پ‚ك‚وپD
پ¦1 پ¦2 “¯ڈم
4.A=(−5, 4)پCP=(3, 2)
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.15
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.037 |
|
** ‚QژںŒ³•½–ت‚ة‚¨‚¯‚é‚Q’¼گü‚ج•½چsڈًŒڈپCگ‚’¼ڈًŒڈ **
پy—v“_پz
•½–تڈم‚ج‚Q’¼گü‚ج•½چsڈًŒڈپCگ‚’¼ڈًŒڈ
پZ•½–تڈم‚ج‚Q’¼گü‚ج–@گüƒxƒNƒgƒ‹ ‚ھ•½چs‚إ‚ ‚é‚ئ‚«پC‚Q’¼گü‚ح•½چs‚ة‚ب‚éپD پZ•½–تڈم‚ج‚Q’¼گü ‚ج–@گüƒxƒNƒgƒ‹ ‚ھگ‚’¼‚إ‚ ‚é‚ئ‚«پC‚Q’¼گü‚حگ‚’¼‚ة‚ب‚éپD |
پi‰ًگàپj گ}‚ً•`‚¯‚خپC–¾‚ç‚©   |
|
5.‚Q’¼گü3x−5y=1, 2x+3y=5‚حگ‚’¼‚إ‚ب‚¢‚±‚ئ‚ًژ¦‚¹پD
پ¦1 پ¦2 “¯ڈم
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.15
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.037
’èگ”چ€1, 5‚حŒ‹‰ت‚ة‰e‹؟‚µ‚ب‚¢پD
ٹeپX‚ج–@گüƒxƒNƒgƒ‹‚ح پ¦پiژQچlپj “ْ–{‚ج’†ٹwچZپCچ‚چZ‚إڈK‚¤2’¼گü‚جگ‚’¼ڈًŒڈ‚حژں‚جŒ`‚ة‚ب‚ء‚ؤ‚¢‚éپD
y=m1x+k1…‡@
‚±‚ê‚ًژg‚ء‚ؤژ¦‚·‚ئy=m2x+k2…‡A ‚ة‚آ‚¢‚ؤ‡@پغ‡A←→m1m2=−1 ‚جŒX‚«‚حپCٹeپX ‚±‚ج‚ئ‚« ‚إ‚ ‚é‚©‚çپC‚±‚ê‚ç‚ج‚Q’¼گü‚حگ‚’¼‚إ‚ب‚¢…پiڈط–¾ڈIپj |
6.ژں‚ج’¼گü‚ج‘g‚ج‚¤‚؟پCگ‚’¼‚ب‚ج‚ح‚ا‚ê‚©پD
(a)پ@3x−5y=1‚ئ2x+y=2
(b)پ@2x+7y=1‚ئx−y=5 (c)پ@3x−5y=1‚ئ5x+3y=7 (d)پ@−x&+y=2‚ئx+y=9
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.16
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.037
’èگ”چ€‚حŒ‹‰ت‚ة‰e‹؟‚µ‚ب‚¢پD
(a) ٹeپX‚ج–@گüƒxƒNƒgƒ‹‚ح (b) ٹeپX‚ج–@گüƒxƒNƒgƒ‹‚ح (c) ٹeپX‚ج–@گüƒxƒNƒgƒ‹‚ح (d) ٹeپX‚ج–@گüƒxƒNƒgƒ‹‚ح ˆبڈم‚ة‚و‚èپC(c)(d)…پi“ڑپj پ¦پiژQچlپj “ْ–{‚ج’†ٹwچZپCچ‚چZ‚إڈK‚¤2’¼گü‚جگ‚’¼ڈًŒڈ
y=m1x+k1…‡@
‚ًژg‚¤‚ئy=m2x+k2…‡A ‚ة‚آ‚¢‚ؤ‡@پغ‡A←→m1m2=−1 (a) (b) (c) (d) ˆبڈم‚ة‚و‚èپC(c)(d)…پi“ڑپj |
|
** ‚RژںŒ³‹َٹش‚ة‚¨‚¯‚镽–ت‚ج•û’ِژ® **
پy—v“_پz
پi‰ًگàپj1“_‚ً’ت‚è—^‚¦‚ç‚ꂽ–@گüƒxƒNƒgƒ‹‚ةگ‚’¼‚ب•½–ت‚ج•û’ِژ®
پZپi‚RژںŒ³‹َٹش‚ة‚¨‚¢‚ؤپj“_پZپi‚RژںŒ³‹َٹش‚ة‚¨‚¢‚ؤپj“_  “_
“_‚¾‚©‚ç ‚ھگ¬‚è—§‚آپD‹t‚àŒ¾‚¦‚éپD ‚±‚ê‚ًگ¬•ھ‚إڈ‘‚‚ئ |
7.ژں‚ج“_‚o‚ً’ت‚èپCƒxƒNƒgƒ‹‚m‚ةگ‚’¼‚ب•½–ت‚ج•û’ِژ®‚ً‹پ‚ك‚وپD
(a)پ@N=(1, −1, 3)P=(4, 2, −1) (b)پ@N=(−3, −2, 4)P=(2, ƒخ, −5) (c)پ@N=(−1, 0, 5)P=(2, 3, 7)
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.16
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.037
(a)پ@1·(x−4)−1·(y−2)+3·(z+1)=0
x−y+3z+1=0…پi“ڑپj (b)پ@−3·(x−2)−2·(y−ƒخ)+4·(z+5)=0 −3x−2y+4z+2ƒخ+26=0…پi“ڑپj (c)پ@−1·(x−2)+0·(y−3)+5·(z−7)=0 −x+5z−33=0…پi“ڑپj |
|
پy—v“_پz
پi‰ًگàپj‚R“_‚ً’ت‚镽–ت‚ج•û’ِژ®
پZپi‚RژںŒ³‹َٹش‚ة‚¨‚¢‚ؤپj‚R“_‚ئ‚¨‚¢‚ؤپC 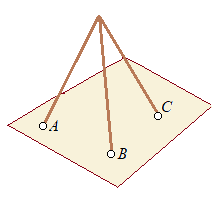 پ@‚R“_‚ھˆê’¼گüڈم‚ة•ہ‚ٌ‚إ‚¢‚éڈêچ‡‚ًڈœ‚¯‚خپC’تڈيپC‚R“_‚ً’ت‚镽–ت‚ح‚½‚¾‚P’ت‚è‚ة’è‚ـ‚éپD
پ@‚R“_‚ھˆê’¼گüڈم‚ة•ہ‚ٌ‚إ‚¢‚éڈêچ‡‚ًڈœ‚¯‚خپC’تڈيپC‚R“_‚ً’ت‚镽–ت‚ح‚½‚¾‚P’ت‚è‚ة’è‚ـ‚éپDپ@—‰ب‚جژہŒ±ٹي‹ï‚â‘ھ—تٹي‹ï‚ب‚اپCگ¸–§‚³‚ھ—v‹پ‚³‚ê‚éٹي‹ï‚ح‚R–{‘«‚ة‚ب‚ء‚ؤ‚¢‚é‚ج‚حپC‚R“_‚ة‚·‚é‚ئ•½–ت‚ھٹm’è‚·‚é‚ئ‚¢‚¤‚±‚ئ‚ً—ک—p‚µ‚½‚à‚ج‚إ‚ ‚éپD
8.ژں‚ج‚R“_‚ً’ت‚镽–ت‚ج•û’ِژ®‚ً‹پ‚ك‚وپD
پi‰ً“ڑپj(a)پ@(2, 1, 1), (3, −1, 1), (4, 1, −1)
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.16
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.037 پ@‹پ‚ك‚镽–ت‚ج•û’ِژ®‚ً ‚ئ‚¨‚پD “_(2, 1, 1)‚ً’ت‚é‚©‚ç “_(3, −1, 1)‚ً’ت‚é‚©‚ç “_(4, 1, −1)‚ً’ت‚é‚©‚ç |
پ@•û’ِژ®‚جŒآگ”پi‚RŒآپj‚ھ–¢’mگ” ‚حپCٹm’肵‚½‰ً‚ًژ‚½‚¸پC•s’è‰ً‚ًژ‚آپD
‚±‚ê‚حپCژں‚ج‚ا‚ج•û’ِژ®‚à“¯‚¶‚à‚ج‚ً•\‚·‚ئ‚¢‚¤‚±‚ئ‚ئ‘خ‰‚µ‚ؤ‚¢‚éپD
کA—§•û’ِژ®(1)(2)(3)‚ً‰ً‚‚ئ‚«‚ةپCچ¬—گ‚ً–h‚®‚½‚ك‚ة‚حپC‚P‚آ‚ج•¶ژڑپC—ل‚¦‚خ‚±‚ج‚و‚¤‚ةپC‹پ‚ك‚é•û’ِژ®‚ح ‚±‚ج‚و‚¤‚ة‚·‚é‚ئپC–¢’mگ”‚ھ3ŒآپC•û’ِژ®‚ھ3Œآ‚جکA—§•û’ِژ®‚ئ‚ب‚èپCچ‚چZ‚إ‰ً‚«ٹµ‚ꂽŒ`‚ة‚ب‚éپD پ@‚ـ‚¸پC(1)−(2), (2)+(3)‚ة‚و‚è (5)‚و‚è (4)‚ة‘م“ü (1)‚ة‘م“ü ˆبڈم‚©‚ç —¼•س‚ً
پ¦
‚ب‚ا‚àپC‚à‚؟‚ë‚ٌ‰ً‚ة‚ب‚é‚ھپC’تڈي‚ح‚ب‚é‚ׂٹب’P‚بگ®گ””ن‚ھچD‚ـ‚ê‚é‚©‚çپCڈم‹L‚جپi“ڑپj‚ھ‚و‚¢پD |
|
(ژQچl1پj پ@‹tچs—ٌ‚ج‹پ‚ك•û‚ًڈK‚ء‚ؤ‚¢‚éڈêچ‡پCڈم‹L‚جکA—§•û’ِژ®‚ًژں‚ج‚و‚¤‚ة‰ً‚‚ئŒ©’ت‚µ‚ھ‚و‚¢ ‚حپCچs—ٌ‚ً—p‚¢‚ؤژں‚جŒ`‚ةڈ‘‚¯‚éپD —¼•س‚ةچ¶‚©‚çŒWگ”چs—ٌ‚ج‹tچs—ٌ‚ًٹ|‚¯‚é‚ئ (ژQچl2پj پ@ƒNƒ‰ƒپپ[ƒ‹‚جŒِژ®‚ًڈK‚ء‚ؤ‚¢‚éڈêچ‡پCڈم‹L‚جکA—§•û’ِژ®‚حژں‚ج‚و‚¤‚ة‰ً‚¯‚é |
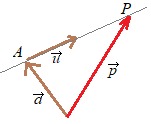 (ژQچl3پj
(ژQچl3پjپZ“_ ‚إ•\‚³‚ê‚éپD‚±‚ê‚ًپCگ¬•ھ •ھ‚¯‚ؤڈ‘‚‚ئ (3)ژ®‚©‚ç”}‰î•دگ” (1)‚ح”Cˆس‚ج’l‚ً‚ئ‚é•دگ”‚ھ‚P‚آ‚ ‚é‚©‚çپCژ©—R“x‚P‚·‚ب‚ي‚؟1ژںŒ³‹َٹشپC’¼گü‚ً•\‚·پD 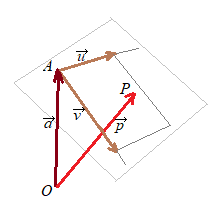 پZ“_
پZ“_‚إ•\‚³‚ê‚éپD‚±‚ê‚ًپCگ¬•ھ ‚ً—p‚¢‚ؤ•\‚·‚ئ •ھ‚¯‚ؤڈ‘‚‚ئ ‚±‚ê‚ç‚©‚çپC‚ـ‚¸”}‰î•دگ” (1’)‚ح”Cˆس‚ج’l‚ً‚ئ‚é•دگ”‚ھ‚Q‚آ‚ ‚é‚©‚çپCژ©—R“x‚Q‚·‚ب‚ي‚؟‚QژںŒ³‹َٹشپC•½–ت‚ً•\‚·پD 8.(a)‚ج–â‘è‚ًپC“_A(2, 1, 1)‚ً’ت‚èƒxƒNƒgƒ‹ •ھ‚¯‚ؤڈ‘‚‚ئ (3’)‚©‚ç”}‰î•دگ” ‚ئ‚ب‚ء‚ؤپC‘Oڈq‚ئ“¯‚¶Œ‹‰ت‚ً“¾‚éپD |
|
8.ژں‚ج‚R“_‚ً’ت‚镽–ت‚ج•û’ِژ®‚ً‹پ‚ك‚وپD
(b)پ@(−2, 3, −1), (2, 2, 3), (−4, −1, 1)
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.16
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.037
پ@‹پ‚ك‚镽–ت‚ج•û’ِژ®‚ً
‚ئ‚¨‚پD ‚±‚جکA—§•û’ِژ®‚ً‰ً‚‚ئ ‚µ‚½‚ھ‚ء‚ؤپC•½–ت‚ج•û’ِژ®‚ح ‚·‚ب‚ي‚؟ |
8.ژں‚ج‚R“_‚ً’ت‚镽–ت‚ج•û’ِژ®‚ً‹پ‚ك‚وپD
(c)پ@(−5, −1, 2), (1, 2, −1), (3, −1, 2)
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.16
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.037
پ@‹پ‚ك‚镽–ت‚ج•û’ِژ®‚ً
‚ئ‚¨‚پD ‚±‚جکA—§•û’ِژ®‚ً‰ً‚‚ئ ‚µ‚½‚ھ‚ء‚ؤپC•½–ت‚ج•û’ِژ®‚ح ‚·‚ب‚ي‚؟ |
|
**‚RژںŒ³‹َٹش‚ة‚¨‚¢‚ؤ‚Q‚آ‚جƒxƒNƒgƒ‹‚ةگ‚’¼‚بƒxƒNƒgƒ‹**
9.(1, 2, −3)‚¨‚و‚ر(2, −1, 3)‚ةگ‚’¼‚بƒxƒNƒgƒ‹‚ً‹پ‚ك‚وپD
پi‰ً“ڑ1پj
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.16
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.038 پ@
پ@‚±‚جکA—§•û’ِژ®(1)(2)‚ً‰ً‚¢‚ؤپCƒxƒNƒgƒ‹
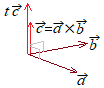 پ@‚»‚ج‚½‚كپC‚±‚ج•û’ِژ®‚حژ©—R“x‚P‚ج•s’è‰ًپi”Cˆس‚ج’l‚ً‚ئ‚é”}‰î•دگ”‚ً‚P‚آٹـ‚ق‰ًپj‚ة‚ب‚éپD
پ@‚»‚ج‚½‚كپC‚±‚ج•û’ِژ®‚حژ©—R“x‚P‚ج•s’è‰ًپi”Cˆس‚ج’l‚ً‚ئ‚é”}‰î•دگ”‚ً‚P‚آٹـ‚ق‰ًپj‚ة‚ب‚éپDپ@‚±‚ê‚حپC‰Eگ}‚ج‚و‚¤‚ة‚ ‚éƒxƒNƒgƒ‹ پ@ژہچغ‚ة‰ً‚‚ئ‚«‚حپC”}‰î•دگ”‚ة‘I‚ش•دگ”‚ً‚P‚آ‘I‚رپC‚»‚ج•¶ژڑ‚إ‘¼‚ج•¶ژڑ‚ً•\‚·‚ئ‚و‚¢پD (1’)+(2’)پ~2 ‚±‚ê‚ً(2’)‚ج‘م“ü ˆبڈم‚©‚ç پi“ڑ1’پj←“–‘RپC‚±‚جŒ`‚إ‚à‚و‚¢پD پi“ڑ2پj←چ‚چZ‚إ‚حپC—ëƒxƒNƒgƒ‹ پi“ڑ3پj←‘هٹw‚إ‚حپC—ëƒxƒNƒgƒ‹‚ح”Cˆس‚جƒxƒNƒgƒ‹‚ةگ‚’¼‚ئ’è‹`‚·‚é‚©‚çپCڈم‹L‚جڈًŒڈ |
پi‰ً“ڑ2پj ‹tچs—ٌ‚ً—p‚¢‚ؤکA—§•û’ِژ®‚ً‰ً‚ڈêچ‡ ‚و‚è —¼•س‚ةچ¶‚©‚çŒWگ”چs—ٌ‚ج‹tچs—ٌ‚ًٹ|‚¯‚é‚ئ ˆب‰؛‚ج“ڑˆؤ‚حپCپi‰ً“ڑ1پj‚ئ“¯—l پi‰ً“ڑ3پj ƒNƒ‰ƒپپ[ƒ‹‚جŒِژ®‚ً—p‚¢‚ؤکA—§•û’ِژ®‚ً‰ً‚ڈêچ‡ ‚ج‰ً‚حپiŒWگ”چs—ٌ‚جچs—ٌژ®‚ھ‚O‚إ‚ب‚¢‚ئ‚«پj ‚ج‰ً‚ح ˆب‰؛‚ج“ڑˆؤ‚حپCپi‰ً“ڑ1پj‚ئ“¯—l پi‰ً“ڑ4پj 
‚Q‚آ‚جƒxƒNƒgƒ‹
|
|
** ‚RژںŒ³‹َٹش‚ة‚¨‚¯‚é‚Q•½–ت‚جŒًگü **
پy—v“_پz
پZپi‚RژںŒ³‹َٹش‚ة‚¨‚¢‚ؤپj“_ ‚±‚ج•û’ِژ®‚ًگ¬•ھ گ¬•ھ‚ة•ھ‚¯‚é‚ئ (3)ژ®‚©‚ç”}‰î•دگ” ‚±‚ج(4)ژ®‚حپCکA—§•û’ِژ® ‚ئŒ©‚邱‚ئ‚ھ‚إ‚«‚éپD (5)‚¨‚و‚ر(6)‚حٹeپX•½–ت‚ج•û’ِژ®‚¾‚©‚çپC‹َٹش‚ة‚¨‚¯‚é’¼گü‚ج•û’ِژ®‚حپC‚Q•½–ت‚جŒًگü‚ئ‚µ‚ؤ•\‚³‚ê‚ؤ‚¢‚邱‚ئ‚ة‚ب‚éپD پZپi‚RژںŒ³‹َٹش‚ة‚¨‚¢‚ؤپj‚Q•½–ت 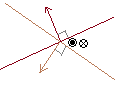 ‚Q‚آ‚ج•½–ت‚ةگ‚’¼‚ب’f–ت‚©‚猩‚½گ} ‚Q‚آ‚ج•½–ت‚ةگ‚’¼‚ب’f–ت‚©‚猩‚½گ}‹Lچ† |
14.‚Q•½–ت2x−y+z=1 , 3x+y+z=2‚جŒًگü‚جƒpƒ‰ƒپپ[ƒ^•û’ِژ®‚ً‹پ‚ك‚وپD(–â‘è12.‘خ‰•ھ)
پi‰ً“ڑ1پj
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.16
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.038 کA—§•û’ِژ® ‚ج‰ً‚ً‹پ‚ك‚éپD•û’ِژ®‚جŒآگ”‚ھ‚QŒآ‚إپC–¢’mگ”‚جŒآگ”‚RŒآ‚و‚è‚à‚PŒآڈ‚ب‚¢‚©‚çپC”}‰î•دگ”‚ً‚PŒآٹـ‚ٌ‚¾•s’è‰ً‚ة‚ب‚éپD‚»‚±‚إپC‚P•¶ژڑ‚ة‚آ‚¢‚ؤ‚ح‰ً‚©‚ب‚¢‚ئŒˆ‚ك‚éپDپi (1)+(2)‚و‚è
کa–َˆّ—pŒ³‚ج‰ً“ڑ‚حپC
‚±‚ê‚ً(1)‚ة‘م“ü‚ئ‚·‚ê‚خ‘خ‰‚·‚é ”}‰î•دگ”‚ً ”}‰î•دگ”‚ً ‚ـ‚½‚ح |
|
پi‰ً“ڑ2پj پ@3ژںŒ³‹َٹش‚ة‚¨‚¯‚é’¼گü‚ج•û’ِژ®‚حپC’ت‚é‚ׂ«‚P“_ پ@2x−y+z=1 , 3x+y+z=2‚ة‚¨‚¢‚ؤپCy=0‚ج‚ئ‚«‚حx=1, z=−1‚ئ‚ب‚é‚©‚çپC“_ پ@‹پ‚ك‚é’¼گü‚ج•ûŒüƒxƒNƒgƒ‹ ‚±‚ê‚ً‰ً‚‚ئ ‚µ‚½‚ھ‚ء‚ؤ ‚P‚آ‚ج•ûŒüƒxƒNƒgƒ‹‚ح |
پi‰ً“ڑ3پj پ@3ژںŒ³‹َٹش‚ة‚¨‚¯‚é’¼گü‚ج•û’ِژ®‚حپC’ت‚é‚ׂ«‚P“_ پi‰ً“ڑ2پj‚ة‚¨‚¢‚ؤپC’ت‚é‚ׂ«‚P“_‚جچہ•W‚ً‹پ‚ك‚ç‚ꂽ–َ‚ًچl‚¦‚ؤ‚ف‚é‚ئپCکA—§•û’ِژ® ‚حپC–¢’mگ”‚ھ3Œآ‚إ‚ ‚é‚ج‚ة‘خ‚µ‚ؤپC•û’ِژ®‚ھ2Œآ‚ئڈ‚ب‚¢‚½‚كپC‚»‚ج‚ـ‚ـ‚إ‚ح•s’è‰ً‚ئ‚ب‚é‚ئ‚±‚ë‚ًپC‚P‚آŒہ’è‚ً’ا‰ء‚µ‚ؤپiy‚ة“ء’è‚ج’l‚ً‘م“ü‚µ‚ؤپC’èگ”‚ة‚µ‚ؤپj–¢’mگ”‚جŒآگ”‚ً2Œآ‚ة‚·‚ê‚خپC“ء’è‚ج“_‚جچہ•W‚ھ’è‚ـ‚邱‚ئ‚ً—ک—p‚µ‚½پD‹ï‘ج“I‚ة‚حپCy=0‚ئ‚·‚é‚ئx=1, z=−1‚ئ‚ب‚邱‚ئ‚©‚çپC“_ پ@‚±‚جچى‹ئ‚ً‚à‚¤1‰ٌچs‚¢پC2‚آ–ع‚ج“_‚ًŒ©‚آ‚¯‚é‚ئ2“_‚`پC‚a‚ھŒ©‚آ‚©‚èپC“_‚`‚ً’ت‚èƒxƒNƒgƒ‹ پ@x=0‚ئ‚·‚é‚ئ پ@‚±‚ج‚ئ‚«پC |
|
14.‚Q•½–ت2x+y+5z=2 , 3x−2y+z=3‚جŒًگü‚جƒpƒ‰ƒپپ[ƒ^•û’ِژ®‚ً‹پ‚ك‚وپD(–â‘è13.‘خ‰•ھ)
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.16
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.038
پi‰ً“ڑ1پj
کA—§•û’ِژ® ‚ج‰ً‚ً‹پ‚ك‚éپD•û’ِژ®‚جŒآگ”‚ھ‚QŒآ‚إپC–¢’mگ”‚جŒآگ”‚RŒآ‚و‚è‚à‚PŒآڈ‚ب‚¢‚©‚çپC”}‰î•دگ”‚ً‚PŒآٹـ‚ٌ‚¾•s’è‰ً‚ة‚ب‚éپD‚»‚±‚إپC‚P•¶ژڑ‚ة‚آ‚¢‚ؤ‚ح‰ً‚©‚ب‚¢‚ئŒˆ‚ك‚éپDپi ”}‰î•دگ”‚ً ”}‰î•دگ”‚ً ‚ـ‚½‚ح |
‘O–â‚ئ“¯—l‚ةپi‰ً“ڑ2پjپi‰ً“ڑ3پj‚ج‚و‚¤‚ة‰ً‚¢‚ؤ‚à‚و‚¢پD‚±‚±‚إ‚حپi‰ً“ڑ3پj‚ًژ¦‚·پD z=0‚ئ‚·‚é‚ئx=1, y=0‚ئ‚ب‚é‚©‚çپC“_A(1, 0, 0)‚ً’ت‚éپD ‚ـ‚½پCx=0‚ئ‚·‚é‚ئ ‚»‚±‚إپC“_A(1, 0, 0)‚ً’ت‚èپC•ûŒüƒxƒNƒgƒ‹ •ûŒüƒxƒNƒgƒ‹‚ئ‚µ‚ؤ |
** ‚RژںŒ³‹َٹش‚ة‚¨‚¢‚ؤ‚Q•½–ت‚ھ‚ب‚·ٹp ** پy—v“_پz
پy—v“_پzپZپi‚RژںŒ³‹َٹش‚ة‚¨‚¢‚ؤپj2•½–ت‚ھ‚ب‚·ٹp‚حپC‚»‚ê‚ç‚ج–@گüƒxƒNƒgƒ‹‚ھ‚ب‚·ٹp‚ة“™‚µ‚¢پD
(پو)‰Eگ}‡@‚ج‚و‚¤‚ب’f–ت‚©‚猩‚½ڈêچ‡پC
‚½‚¾‚µپC‡A‚ج‚و‚¤‚ة–@گüƒxƒNƒgƒ‹‚جŒü‚«‚ة‚و‚ء‚ؤ‚حپC90پ‹<ƒئپ…180پ‹‚ة‚ب‚ء‚ؤ‚µ‚ـ‚¤ڈêچ‡‚ھ‚ ‚éپDƒئ+ƒس=90پ‹ ƒئ’+ƒس=90پ‹ ‚¾‚©‚ç ƒئ=ƒئ’ ‚ھگ¬‚è—§‚آ پ@چ‚چZ‚إ‚حپC2•½–ت‚ج‚ب‚·ٹp‚حپC0پ‹پ…ƒئپ…90پ‹‚ئ90پ‹<ƒئپ…180پ‹‚ج‚Q‚آ‚ ‚邤‚؟‚جڈ¬‚³‚¢•ûپC0پ‹پ…ƒئپ…90پ‹‚إ“ڑ‚¦‚é‚ج‚ھ•پ’ت‚إ‚ ‚éپD پiپ¦ƒ‰ƒ“ƒO‚جکa–َ‚إ‚حپC–@گüƒxƒNƒgƒ‹‚ھ‚ب‚·ٹp‚»‚ج‚ـ‚ـ•½‹C‚إ“ڑ‚¦‚é‚و‚¤‚ة‚ب‚ء‚ؤ‚¢‚éپj ‚¾‚©‚ç ‚½‚¾‚µپCچ‚چZ‚إ‚ح |
15.ژں‚ج‚Q•½–ت‚ج‚ب‚·ٹp‚ج—]Œ·‚ً‹پ‚ك‚و
(a)پ@x+y+z=1 , x−y−z=5
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.16
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.039 |
|
15.ژں‚ج‚Q•½–ت‚ج‚ب‚·ٹp‚ج—]Œ·‚ً‹پ‚ك‚و
(c)پ@x+2y−z=1 , −x+3y+z=2
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.16
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.039 |
15.ژں‚ج‚Q•½–ت‚ج‚ب‚·ٹp‚ج—]Œ·‚ً‹پ‚ك‚و
(d)پ@2x+y+z=3 , −x−y+z=ƒخ
پiˆّ—pŒ³پjSerge LangپuLINEAR ALGEBRAپv1پک5,P.16
پiکa–َˆّ—pŒ³پjƒ‰ƒ“ƒOپuگüŒ`‘مگ”ٹw(ڈم)پv1ڈحپک5, P.039 |