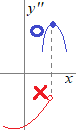
�i�Q�l�j
�@f ’(a)=0����f ”(a)�����i���j�̂Ƃ��Cf(a)�͋ɏ��l�i�ɑ�l�j�ƌ����܂����Cf ”(a)���O�Ȃ�ɒl���ǂ�������ł��܂���D
�@���̏ꍇ�́C����ɑ�3���������g���ċ��߂邱�Ƃ��ł��܂��D
�@��ʂɁC��P����������悎�������܂ł��ׂĂO�ŁC��n+1�������������̂����ꂩ�ł���Ƃ��C�ɒl���ۂ��肷�邱�Ƃ��ł��܂��D
(1) f ’(a)=0, f ”(a)=0����f (3)(a)>0�̂Ƃ�
f (n)(x)�͑悎��������\���L���ł�
| x |
| a |
|
| y' | (A)
+ | (B)
0 | (C)
+ |
| y'' | (D)
− | (E)
0 | (F)
+ |
}) \( \displaystyle y^{(3)} \) \( \displaystyle y^{(3)} \) | (G)
+ | (H)
+ | (I)
+ |
| y | (J)
 \( \displaystyle \nearrow \) \( \displaystyle \nearrow \) | (K)
f(a) | (L)
 \( \displaystyle \nearrow \) \( \displaystyle \nearrow \) |
�@�O�ɂ�����c�_���v���o���ƁC���̂悤�ɕ��������܂��Ă����܂��D
�@(H)���{�Ŕ����\������C(G)���{�ɂȂ�C(E)���O������C(D)�̂Ƃ���́u�����ĂO�ɂȂ�̂�����v����܂ł�−�ł��������ƂɂȂ�܂��D
�@���ɁC(D)��−��(B)���O������C(A)�̂Ƃ���́u�����ĂO�ɂȂ�̂�����v����܂ł́{�ł��������ƂɂȂ�܂��D
�@�E�����́C(I)���{��(E)���O������C(F)�̂Ƃ���́u�O���瑝����̂�����v��������́{�ɂȂ�܂��D
�@����ɁC(F)���{��(B)���O������C(C)�̂Ƃ���́u�O���瑝����̂�����v��������́{�ɂȂ�܂��D
�@���ǁC(A)���{,(C)���{�ƂȂ��āCf(a)�͋ɒl�ł͂Ȃ����Ƃ�������܂��D
�Ⴆ��f(x)=x3�̂Ƃ��Cf’(x)=3x2, f”(x)=6x,
f (3)(x)=6������Cf’(0)=0, f”(0)=0, f (3)(0)>0�ƂȂ�܂����Cf(0)=0�͋ɒl�ł͂���܂���D
(2) f ’(a)=0, f ”(a)=0, f (3)(a)=0����f (4)(a)>0�̂Ƃ�
| x |
| a |
|
| y' | (A)
− | (B)
0 | (C)
+ |
| y'' | (D)
+ | (E)
0 | (F)
+ |
}) \( \displaystyle y^{(3)} \) \( \displaystyle y^{(3)} \) | (G)
− | (H)
0 | (I)
+ |
}) \( \displaystyle y^{(4)} \) \( \displaystyle y^{(4)} \) | (J)
+ | (K)
+ | (L)
+ |
| y | (M)
 \( \displaystyle \searrow \) \( \displaystyle \searrow \) | (N)
f(a) | (O)
 \( \displaystyle \nearrow \) \( \displaystyle \nearrow \) |
�@(K)���{�Ŕ����\������C(J)���{�ɂȂ�C(H)���O������C(G)�̂Ƃ���́u�����ĂO�ɂȂ�̂�����v����܂ł�−�ł��������ƂɂȂ�܂��D
�@���ɁC(G)��−��(E)���O������C(D)�̂Ƃ���́u�����ĂO�ɂȂ�̂�����v����܂ł́{�ł��������ƂɂȂ�܂��D
�@����ɁC(D)���{��(B)���O������C(A)�̂Ƃ���́u�����ĂO�ɂȂ�̂�����v����܂ł�−�ł��������ƂɂȂ�܂��D
�@�E�����́C(L)���{��(H)���O������C(I)�̂Ƃ���́u�O���瑝����̂�����v��������́{�ɂȂ�܂��D
�@����ɁC(I)���{��(E)���O������C(F)�̂Ƃ���́u�O���瑝����̂�����v��������́{�ɂȂ�܂��D
�@����ɁC(F)���{��(B)���O������C(C)�̂Ƃ���́u�O���瑝����̂�����v��������́{�ɂȂ�܂��D
�@���ǁC(A)��−,(C)�́{�ƂȂ��āCf(a)�͋ɏ��l�ł��邱�Ƃ�������܂��D
�Ⴆ��f(x)=x4�̂Ƃ��Cf’(x)=4x3, f”(x)=12x2,
f (3)(x)=24x, f (4)(x)=24������Cf’(0)=0, f”(0)=0, f (3)(0)=0, f (4)(0)>0�ƂȂ�Cf(0)=0�͋ɏ��l�ɂȂ�܂��D
(*) �ȏ�̋c�_��U��Ԃ��Ă݂�ƁC�E�����̕�����
f (n)(0)�̕����Ɉ�v���Ă��邱�Ƃ�������܂��D�O���瑝����i�t�̏ꍇ�͌���j����������D
�@�������́C�u�����ĂO�ɂȂ�v�u�����ĂO�ɂȂ�v����シ��̂ŁC�{��−�����݂ɓo�ꂷ�邱�Ƃ�������܂��D
�@�ȏ�̌��ʂ��܂Ƃ߂�ƁCf’(a)=0, f”(a)=0, f (3)(a)=0, … , f (2n−1)(a)=0, f (2n)(a)>0�̂Ƃ��Cf(a)�͋ɏ��l
�@f’(a)=0, f”(a)=0, f (3)(a)=0, … , f (2n)(a)=0,
f (2n+1)(a)>0�̂Ƃ��Cf(a)�͋ɒl�ł͂Ȃ��ƌ����܂��D
(**) f’(a)=0, f”(a)=0, f (3)(a)=0, … , f (2n−1)(a)=0,
f (2n)(a)<0�̂Ƃ����̏ꍇ�ɂ��ẮC�ȏ�̋c�_�ƕ������t�ɂȂ�܂��D
|
 (1) ���l�ɂ��āC���铱��f ’(x)�̓���f ”(x)���Cf ”(x)>0�ƂȂ��Ԃɂ����āC����f ’(x)�͑������܂��D
(1) ���l�ɂ��āC���铱��f ’(x)�̓���f ”(x)���Cf ”(x)>0�ƂȂ��Ԃɂ����āC����f ’(x)�͑������܂��D (2) �t�ɁC���铱��f ’(x)�̓���f ”(x)���Cf ”(x)<0�ƂȂ��Ԃɂ����āC����f ’(x)�͌������܂��D
(2) �t�ɁC���铱��f ’(x)�̓���f ”(x)���Cf ”(x)<0�ƂȂ��Ԃɂ����āC����f ’(x)�͌������܂��D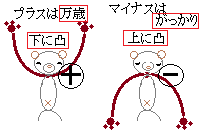
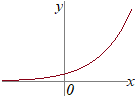 �i�j
�i�j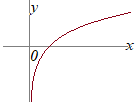 �i�j
�i�j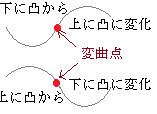
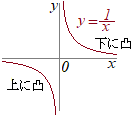 �i�Q�l�j
�i�Q�l�j